ФІЗИКА. Вчимося розв'язувати задачі. "ОПТИКА". Компенсаційний курс
2. Приклади розв’язування задач
2.3. Формули дзеркала і лінзи
Задача 2.16. Рефлектор прожектора являє собою вгнуте сферичне дзеркало з радіусом кривини R = 30 см. Визначити на якій відстані l від його фокуса на головній оптичній осі слід розмістити точкове джерело світла, аби одержати конічний пучок променів із точкою сходження на відстані L = 10 м від полюса.
Задача 2.17. Промені збіжного конічного пучка, що проходять крізь розсіювальну лінзу з фокусною відстанню F = 30 см, перетинаються на головній оптичній осі на відстані L = 60 см від лінзи. Визначити, на яку відстань l зміститься точка сходження променів, якщо лінзу прибрати.
Задача 2.18. Мураха повзе вздовж головної оптичної осі опуклого дзеркала із фокусною відстанню F зі швидкістю v = 5 мм/с. Побудувати зображення мурахи та визначити швидкість його руху u на момент знаходження мурахи на відстані d = 1,5F від дзеркала.
Задача 2.19. Малий предмет розглядають крізь лупу із фокусною відстанню F = 5 см так, що зображення утворюється на відстані найкращого зору L = 25 см. Визначити, на якій відстані d від предмета розташовано лупу, та яке збільшення \(\Gamma\) вона дає.
Задача 2.20. Визначити: а) при якій відстані d0 від предмета до лінзи з фокусною відстанню F відстань L між ним і його зображенням на екрані буде мінімальною та б) її величину L0.
Задача 2.21. Лінза дає чітке зображення джерела світла на екрані в двох положеннях на відстані l = 60 см одне від одного. Визначити фокусну відстань лінзи F, якщо відстань від неї до екрана L = 1 м.
Задача 2.22. Короткозора людина читає книжку, тримаючи її на відстані d = 16 см від очей, тоді як відстань найкращого зору складає d0 = 25 см. Визначити оптичну силу Dc окулярів, які їй потрібні для корекції зору.
Задача 2.23. На одній осі зі збиральною лінзою Л1 із заданою фокусною відстанню F1 встановлено розсіювальну лінзу Л2. Визначити її фокусну відстань F2, якщо система створює збільшене в \(\Gamma=2\) рази дійсне зображення предмета, котрий розміщено перед збиральною лінзою на відстані d1 = 3F1.
Задача 2.16
Рефлектор прожектора являє собою вгнуте сферичне дзеркало з радіусом кривини R = 30 см.
Визначити,
на якій відстані l від фокуса дзеркала на головній оптичній осі слід розмістити точкове джерело світла, аби одержати конічний пучок променів із точкою сходження на відстані L = 10 м від полюса.
|
Дано: R = 30 см = 0,3 м
L = 10 м
|
|
l - ?
|
Розв’язання
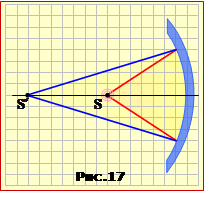 Положення джерела S і точки сходження S′ відбитого пучка схематично (без дотримання співвідношеь між відстанями) показані на рис. 17, з якого зрозуміло, що точка S′ є дійсним зображенням джерела S (див. п.1.3), котре є віддалене від полюса дзеркала на відстань f = L, а відстань d від самого джерела S до полюса перевищує фокусну відстань F на шукану величину l: d = F + l. Отже, згідно з формулою дзеркала (1.6),
Положення джерела S і точки сходження S′ відбитого пучка схематично (без дотримання співвідношеь між відстанями) показані на рис. 17, з якого зрозуміло, що точка S′ є дійсним зображенням джерела S (див. п.1.3), котре є віддалене від полюса дзеркала на відстань f = L, а відстань d від самого джерела S до полюса перевищує фокусну відстань F на шукану величину l: d = F + l. Отже, згідно з формулою дзеркала (1.6),
\(\frac{1}{F+l}+\frac{1}{L}=\frac{1}{F}\).
Звідси після елементарних викладок одержимо
\(l=\frac{F^{2}}{L-F}\),
і, відтак урахувавши формулу (1.5), дістанемо наступну точну відповідь:
\(l=\frac{R^{2}}{2(2L-R)}\).
Але, позаяк за умовою R << L, обчислення доцільно виконувати за наближеним виразом:
$f\approx \frac{{{R}^{2}}}{4L}$ = 4 мм
Отже, джерело має бути розташоване за полюсом на 4 мм далі від дзеркала, як це разом із побудовою зображення точки S′ показано на рис. 17-1.
Задача 2.17
Промені збіжного конічного пучка, що проходять крізь розсіювальну лінзу з фокусною відстанню F = 30 см, перетинаються на головній оптичній осі на відстані L = 60 см від лінзи.
Визначити,
на яку відстань l зміститься точка сходження променів, якщо лінзу прибрати.
|
Дано: F = 30 см
L = 60 см
|
|
l - ? |
Розв’язання
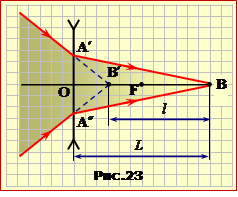
Збіжні промені, що падають на лінзу, йдуть від не точкового джерела. Тож може здатися, що формула лінзи (1.6) є недійсною через невизначеність відстані d. Але завдяки оборотності світлових променів задачу можна "обернути", розглядаючи точку точку сходження самих променів як джерело, а точку сходження продовжень – як його уявне зображення (рис. 23-1), та покласти у формулі (1.6) d = L і f = L – l. Тоді, врахувавши правило знаків, після елементарних перетворень отримаємо відповідь задачі:
|
|
\(\frac{1}{L}-\frac{1}{L-l}=-\frac{1}{F}\) \(\Rightarrow\) \(l=\frac{L^{2}}{L+F}=40\) см. |
(1) |
На завершення зауважимо, що, позаяк порядок доданків у рівнянні (1) не має значення, точку сходження продовжень променів можна формально трактувати як уявний "предмет", а точку сходження самих променів — як його дійсне зображення. Тоді у формулі лінзи –(L – l)= d′ і L = f′.
Задача 2.18
Мураха повзе вздовж головної оптичної осі опуклого дзеркала із фокусною відстанню F зі швидкістю v = 5 мм/с.
1) побудувати зображення мурахи та
2) визначити швидкість його руху u на момент знаходження мурахи на відстані d = 1,5F від дзеркала.
|
Дано: v = 5 мм/с
d = 1,5F
|
|
u - ?
|
Розв’язання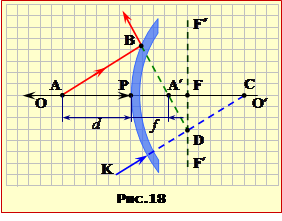
1. Зображення (рис. 18) будуємо в такій послідовності за рекомендаціями (п.1.4, рис. 2.15б):
1) показуємо положення фокальної площини F′F″, яка перетинає головну оптичну вісь ОО′ в точці F на середині радіуса кривини PС дзеркала (ф-ла (1.5));
2) проводимо допоміжний промінь KC у напрямі до центра кривини C дзеркала, і відмічаємо точку перетину D його продовження з фокальною площиною.
3) будуємо хід паралельного до KC допоміжного променя АВ, продовження якого після відбивання теж проходить через точку D;
4) другий необхідний для побудови зображення промінь AP напрямляємо вздовж головної оптичної осі ОО′, тож у точці P він відбивається в протилежному напрямі;
5) у точці перетину A′ продовжень BD і РC указаних ”робочих“ променів отримуємо уявне зображення точки A.
2. Для визначення швидкості зображення u спочатку за формулою (1.10) виразимо зв'язок між координатами (відстанями від дзеркала) f і d, врахувавши, що для опуклого дзеркала f < 0 і d < 0 :
|
$-\frac{1}{F}=\frac{1}{{{d}}}-\frac{1}{f}\quad \Rightarrow \quad f=\frac{Fd}{{{d}}+F}$. |
(1) |
З цього виразу видно, що величина f не є прямо пропорційна до d, отже, на відміну від мурахи, її зображення рухається нерівномірно. Через це шукана швидкість u визначається похідною по часу f′ величини f : u = f′ (див. [І], розділ І, п.1.1). Тож, із виразу (1) за правилом диференціювання частки, отримаємо:
| $u=F\frac{\left( {d}'\left( d+F \right)-d{{\left( d+F \right)}^{\prime }} \right)}{{{\left( d+F \right)}^{2}}}={{\left( \frac{F}{d+F} \right)}^{2}}{d}'$, |
(2) |
Відтак, урахувавши, щоде d′ = $v$ і d = 1,5F, дістанемо наступну відповідь:
|
$u=\frac{v}{{{2,5}^{2}}}=0,8$ мм/с |
(3) |
Отриманий результат показує, що опукле дзеркало дає зменшені не лише розміри зображення, а й швидкісь його руху.
Покажемо також, як можна розв'язати задачу без вищої математики.
Задля цього спочатку за допомогою виразу (1) запишемо наближений вираз шуканої швидкості u ≈ (Δf/Δt) при невеликому переміщенні мурахи відносно дзеркала з відстані d до d + $\Delta d$:
|
$u\approx \frac{F}{\Delta t}\left( \frac{d+v\Delta t}{d+v\Delta t+F}-\frac{d}{d+F} \right)$. |
Відтак, звівши вираз у дужках до спільного знаменника й узявши до уваги, що $\Delta d=v\Delta t$, після спрощень отримаємо
|
$u\approx \frac{{{F}^{2}}v}{\left( d+F \right)\left( d+v\Delta t+F \right)}$ |
|
Зрозуміло, що точність цього виразу при зменшенні проміжку часу, для якого його отрмано, зростатає. Тож у границі $\Delta t\to 0$ він дає точну відповідь, яка збігається з (3).
Малий предмет розглядають крізь лупу із фокусною відстанню F = 5 см так, що зображення утворюється на відстані найкращого зору L = 25 см.
Визначити,
на якій відстані d від предмета розташовано лупу, та яке збільшення \(\Gamma\) вона дає.
|
Дано: F = 5 см
L = 25 см
|
|
d, \(\Gamma\) - ?
|
Розв’язання
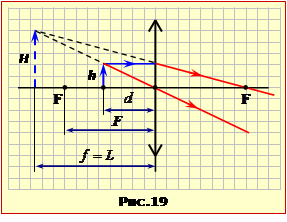
Лупа – то є збирвльна лінза, котра "озброює" око, тобто створює збільшене пряме (неперевернуте) зображення предмета, що розглядається. Таке зображення є уявним (див. п. 1. 3), тому лупа має бути розміщена біля ока на відстані від предмета d < F , аби відстань до зображення складала f = L, як показано на рис. 19. Тож, із формули лінзи (1.6) з урахуванням правила знаків (див. п. 1. 3) отримуємо:
|
\(\frac{1}{d}-\frac{1}{L}=\frac{1}{F}\) \(\Rightarrow\) \(d=\frac{LF}{L+F}\) $\approx $4,2 см. |
(1) |
Відповідно, для збільшення Γ= (L/d) виходить
\(\Gamma=\frac{L+F}{F}\) = 6
Задача 2.20
Визначити:
а) при якій відстані d0 від предмета до лінзи з фокусною відстанню F відстань L між ним і його зображенням на екрані буде мінімальною та
 б) її величину L0.
б) її величину L0.
|
Дано: F
|
|
d0 - ?
L0 - ?
|
Розв’язання
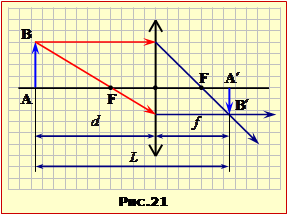
Найперше зауважимо, що побачити на екрані можна тільки дійсне зображення. Отже, лінза є збиральною, а предмет розташовано за фокусом, як показано на рис. 21.
Аби знайти загальну відповідь, спочатку встановимо зв'язок між відстанями від предмета до лінзиі d та до зображення (екрана) L, виразивши у формулі лінзи (1.6) відстань f від лінзи до зображення, як
| f = L – d. |
|
Тоді
|
\(\frac{1}{d}+\frac{1}{L-d}=\frac{1}{F}\) \(\Rightarrow\) \(L=\frac{d^{2}}{d-F}\). |
(1) |
Подальший розв'язок можна провести в два способи, використавши:
1. Вищу математику;
2. Алгебру.
Спосіб 1
а) У точці мінімуму функція переходить від спаду до зростання, тому швидкість її зміни, що визначається похідною, дорівнює нулю. Отже, аби отримати відповіді, треба знайти похідну L′(d) функції (1) і прирівняти її до нуля. А саме.
Вираз (1) є часткою функцій φ1 = d2 і φ2 = (F – d). Тож за правилом диференціювання частки
${{\left( \frac{{{\varphi }_{1}}}{{{\varphi }_{2}}} \right)}^{\prime }}=\frac{{{\varphi }_{1}}^{\prime }{{\varphi }_{2}}-{{\varphi }_{1}}{{\varphi }_{2}}^{\prime }}{\varphi _{2}^{2}}$,
і, враховуючи, що ${{\varphi }_{1}}^{\prime }=2d$ i ${{\varphi }_{2}}^{\prime }=1$,
|
\(L^{\prime}=\frac{2d(d-F)-d^{2}}{(d-F)^{2}}=\frac{d(d-2F)}{(d-F)^{2}}\). |
|
Відтак, прирівнявши отриманий вираз до нуля при d = d0, знайдемо першу відповідь:
|
\(\frac{d_{0}( d_{0}-2F)}{( d_{0}-F)}=0\) \(\Rightarrow\) \(d_{0}=2F\). |
|
б) Другу відповідь (величину L0) знайдемо підстановкою \(d = d_{0}=2F\) у вираз (1):
\(L_{0}=\frac{4F^{2}}{2F-F}=4F\).
Принагідно зауважимо, що при отриманих відстанях L0 = 4F (1) і d0 = 2F також і відстань f = 2F. Отже, мінімальна відстань між предметом і його дійсним зображенням спостерігається при їхньому симетричному розташуванню на подвійній фокусній відстані від лінзи.
Спосіб 2
Перепишемо вираз (1) у вигляді квадратного рівняння
|
\(d^{2}-Ld+LF=0\), |
|
корені якого
|
\(d_{1,2}=\frac{L}{2}\left(1\pm\sqrt{1-\frac{4F}{L}}\right)\) |
(2) |
мають бути дійсними бо визначають положення дійсного зображення. Тому лише за умови
\(1-\frac{4F}{L}\ge{0}\) \(\Rightarrow\) \(L\ge{4F}\).
Отже, мінімальна можлива відстань між предметом та його зображенням на екрані (відповідь б)) складає
\(L_{0}=4F\)
і залежить тільки від фокусної відстані лінзи.
Підставивши це значення у вираз (2), дістанемо відповідь а):
\(d_{0}=\frac{L_{0}}{2}=2F\).
Задача 2.21
Лінза дає чітке зображення джерела світла на екрані в двох положеннях на відстані l = 60 см одне від одного.
Визначити
фокусну відстань лінзи F, якщо відстань від неї до екрана L = 1 м.
|
Дано: L = 1 м
l = 60 см
|
|
F - ?
|
Розв’язання
Одразу візьмемо до уваги, що на екрані може утворюватися тільки дійсне зображення, тож лінза є збиральною. 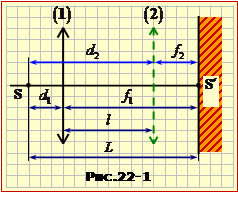
На рис. 22-1 схематично показані точка S, її зображення S′, відповідні положення лінзи та позначені всі потрібні відстані.
Для отримання відповіді простіше за все для кожного випадку записати з урахуванням знаків формулу лінзи (1.6) та відповідно до умови – співвідношеня між величинами, що входять до неї:
|
\(\frac{1}{d_{1}}+\frac{1}{f_{1}}=\frac{1}{F}\) |
(1) |
|
|
\(\frac{1}{d_{2}}+\frac{2}{f_{2}}=\frac{1}{F}\) |
(2) |
|
|
${{f}_{1}}+{{d}_{1}}=L$ |
(3) |
|
|
${{f}_{2}}+{{d}_{2}}=L$ |
(4) | |
|
${{d}_{2}}-{{d}_{1}}=l$ |
(5) |
В отриманій системі рівнянь кількість невідомих (d1, f1, d2, f2, F) збігається із кількістю рівнянь, отже вона є повною. Тож, розв'язавши її, можна серед інших отримати й шукану величину F. Але такий підхід вимагає громіздких викладок і є нераціональним. Натомість доцільно скористатись одним із застосованих у попередній задачі способів, а саме.
I спосіб. Завдяки оборотності світлових променів (п. 1.3), зробивши в рівнянні (5) заміну d2 = f1 , f2 = d1, отримаємо:
|
\(f_{1}-d_{1}=l\), |
(5′) |
і почленно додавши та віднявши рівняння (5′) та (3), дістанемо
\(d_{1}=\frac{L-l}{2}\), \(f_{1}=\frac{L+l}{2}\).
Відтак, підставивши ці вирази в рівняння (1), після нескладних викладок знайдемо відповідь:
\(\frac{2}{L-l}+\frac{2}{L+l}=\frac{1}{F}\) \(\Rightarrow\) \(F=\frac{L^{2}-l^{2}}{4l}=16\) см.
II спосіб. Скористаємось виразами d1 і d2 із задачі 2.19 (формула (6)):
\(d_{1}=\frac{L}{2}\left(1-\sqrt{1-\frac{4F}{L}}\right)\),
\(d_{2}=\frac{L}{2}\left(1+\sqrt{1-\frac{4F}{L}}\right)\).
В такому разі, згідно з співвідношенням (3)
\(l=L\sqrt{1-\frac{4F}{L}}\) \(\Rightarrow\) \(F=\frac{L^{2}-l^{2}}{4L}\) = 16 см.
Задача 2.22
Короткозора людина читає книжку, тримаючи її на відстані d = 16 см від ока, тоді як відстань найкращого зору складає d0 = 25 см.
Визначити
оптичну силу Dc окулярів, які їй потрібні для корекції зору.
|
Дано: d = 16 см
d0 = 25 см
|
|
Dc - ?
|
Розв’язання
Із фізичної точки зору око являє собою збиральну лінзу (кришталик), котра розташована на приблизно однаковій для всіх людей відстані від ″екрана″ (сітківки) такій, що чітке зображення на ній утворюється при відстані від кришталика до предмета d0 = 25 см, яка називається відстанню найкращого зору. Але в людей з дефектами зору ця відстань інша, й це створює великі незручності та перевтомлює око. Тож задля корекції зору поблизу ока розміщують окуляри – допоміжні лінзи, що разом з кришталиком утворюють систему з необхідною для нормального зору оптичною силою (оберненою фокусною відстанню (1.12)), котра дорівнює
|
|
D0 = D + Dc, |
де D і Dc – оптичні сили кришталика та коригуючих лінз (окулярів) нарізно.
Ясна річ, при читанні й з окулярами, і без них, чітке зображення утворюється на одній і тій самій відстані f від кришталика до сітківки ока. Отже, за формулою лінзи (1.6) маємо
|
|
$\frac{1}{{{d}_{0}}}+\frac{1}{f}=D+{{D}_{c}}$, |
|
$\frac{1}{d}+\frac{1}{f}=D$, |
звідки випливає така відповідь:
\(D_{c}=\frac{1}{d}-\frac{1}{d_{0}}=-2,25\) дптр.
Знак ″–″ означає, що для короткозорих людей окуляри виготовляються із розсіювальних лінз.
Задача 2.23
 На одній осі зі збиральною лінзою Л1 із заданою фокусною відстанню F1 у фокальній площині встановлено розсіювальну лінзу Л2.
На одній осі зі збиральною лінзою Л1 із заданою фокусною відстанню F1 у фокальній площині встановлено розсіювальну лінзу Л2.
Визначити
її фокусну відстань F2, якщо система створює збільшене в \(\Gamma=2\) рази дійсне зображення предмета, котрий розміщено перед збиральною лінзою на відстані d1 = 3F1.
|
Дано: d1 = 3F1
\(\Gamma=2\)
|
|
F2 - ?
|
Розв’язання
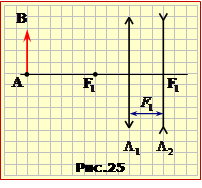
На рис. 25 показано взаємне розташування предмета й лінз, а на на рис. 25-1 — хід променів і необхідні для розрахунку величини F2 відстані.
Ключовою при розрахунку оптичної системи є оборотність променів (див. п. 1.3), що дозволяє віртуальне зображення від одного елемента системи трактувати як зображуваний предмет для наступного. Тому в даній задачі дійсне зображення A2B2 можна розглядати як предмет, а стрілку A1B1 – як його уявне зображення в розсіювальній лінзі Л2. Тож величину F2 будемо шукати за формулою (1.10) із відповідним урахуваням правила знаків (п. 1.3):
|
$-\frac{1}{{{d}_{2}}}+\frac{1}{{{f}_{2}}}=-\frac{1}{{{F}_{2}}}$. |
(1) |
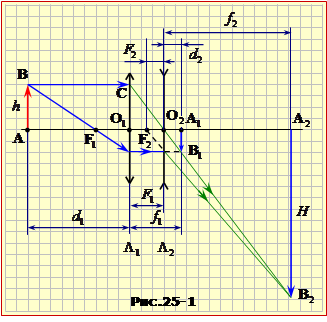
Потрібні для цього величини d2, f2 знайдемо, розглянувши хід променів, рис. 25-1. А саме, з подібності трикутників O2A2B2 і O2O1C випливає, що
$\frac{{{f}_{2}}}{{{F}_{1}}}=\frac{H}{h}\quad \Rightarrow \quad {{f}_{2}}=\Gamma {{F}_{1}}$.
А для визначення величини d2 спочатку за формулою (1.10) знайдемо значення f1, урахувавши, що d1 = 3F1:
|
|
\(\frac{1}{3F_{1}}+\frac{1}{f_{1}}=\frac{1}{F_{1}}\) \(\Rightarrow\) \(f_{1}=\frac{3}{2}F_{1}\). |
|
Отже, позаяк d2 = f1 – F1,
${{d}_{2}}=\frac{1}{2}{{F}_{1}}$.
Відтак підставимо цю величину та знайдене раніше значення ${{f}_{2}}=\Gamma {{F}_{1}}$ у вираз (1) й отримаємо наступну відповідь:
$-\frac{2}{{{F}_{1}}}+\frac{1}{\Gamma {{F}_{1}}}=-\frac{1}{{{F}_{2}}}\quad \Rightarrow \quad {{F}_{2}}=\frac{2}{3}{{F}_{1}}$