ФІЗИКА. Вчимося розв'язувати задачі. "КОЛИВАННЯ ТА ХВИЛІ". Компенсаційний курс

2. Приклади розв'язування задач

Задача 3.1. У плоскій хвилі, що поширюється зі швидкістю v = 2 м/с, коливання в точці А (рис. 1)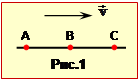 відбуваються відповідно до рівняння см. Визначити зміщення $\xi$ та швидкість коливань u в точках В і С на відстані l₁ = 30 см і l₂ = 45 см від т. А на момент $\tau$ =1 с.

Задача 3.2. Хвилі від катера, що пливе озером, дістаються берега за час t = 0,5 хв і накочуються на нього з інтервалом часу $\tau=0,8$ с.Визначити відстань L від катера до берега, якщо відстань між гребенями хвиль l = 2 м.

Задача 3.3. Визначити швидкість поширення v монохроматичної хвилі з частотою $\nu=10$ Гц, якщо на промені в точках на відстані $\Delta{l}=100$ см одна від одної різниця фаз дорівнює $\Delta\varphi=\pi/4$ .

Задача 3.4. Відстань між гребенями хвиль на морі l = 5 м. Коли катер йде в напрямку поширення хвиль, вони б'ють у ніс катера з частотою n₁ = 2 удари за секунду. Якщо ж катер рухається назустріч, то удари йдуть з частотою n₂ = 4 удари за секунду. Визначити швидкість поширення хвиль v та швидкість катера V.

Задача 3.5. Літак рухається на висоті H = 4 км з надзвуковою швидкістю. Визначити швидкість V літака, якщо спостерігач на землі почув його через $\tau= 10$ c після того, як побачив прямо над собою. Швидкість звуку v = 330 м/с.

Задача 3.6. З рухомого потяга подають звуковий сигнал з частотою $\nu_{0}=400$ Гц. Визначити швидкість V та напрям руху потяга, якщо людина, що вийшла на перон, почула сигнал потяга частотою $\nu=380$ Гц. Швидкість звуку v = 340 м/с.

$V$ , якщо для машиніста частота сигналу складає ${{\nu }}$ = 470 Гц. Швидкість звуку v = 335 м/с.

Визначити частоту сигналу ${{\nu }_{I}}$ і яку сприймає кожен водій при швидкості звуку ${{v}}$ = 340 м/с.

Задача 3.1.

У плоскій хвилі, що поширюється зі швидкістю $v=0,7$ м/с, коливання в точці А (рис. 1) відбуваються відповідно до рівняння ${{\xi }_{A}}=5\sin 5\pi t$ , см.

Визначити

зміщення $\xi$ та швидкість коливань u в точках В і С на відстані l₁ = 30 см і l₂ = 45 см від т. О на момент $\tau$ = 1 с.

Дано:

${{\xi }_{A}}=5\sin 5\pi t$ , см

${{l}_{1}}=30$ см

${{l}_{2}}=45$ см

$v=0,7$ м/с

$\tau$ = 1 с

${\xi }_{B,C}$ –?
${{u}_{B,C}}$ –?

Розв’язання

В умові рівняння коливань задано в числовій формі, тож їхня амплітуда А = 5 см і частота

$\nu = 2,5$ Гц. А позаяк коливання подано через функцією sin, загальне рівняння хвилі (п. 1.1переробити)

зручно записати як

$\xi \left( x,t \right)=A\sin \left( 2\pi \nu \left( t-\frac{x}{v} \right) \right)$ .

(1)

Відтак, прийнявши т. А за початок відліку, отримаємо наступний вираз для величина

${\xi }$ на заданій відстані х = l і в заданий момент часу t = τ :

$\xi =\text{A}\sin \left( 2\pi \nu \left( \tau -\frac{l}{v} \right) \right)$ .

(1а)

Швидкість коливань, яка є похідною зміщення по часу: $u={\xi }'\left( t \right)$ , згідно з рівнянням (1) визначається як

$u\left( x,t \right)=2\pi \nu A\cos \left( 2\pi \nu \left( t-\frac{x}{v} \right) \right)$ ,

(2)

і при х = l та t = τ складає:

$u=2\pi \nu A\cos \left( 2\pi \nu \left( \tau -\frac{l}{v} \right) \right)$ .

(2а)

Відтак, підставивши у вирази (1а) і (2а) задані числові дані, отримуємо наступні відповіді:

${\xi }_{1}$ = 2,1 см; ${\xi }_{2}$ = –3,1 см/с.
${{u}_{1}}$ = –71,1 см/с; ${{u}_{2}}$ = 61,4 см/с.

Знаки в отриманих відповідях свідчать про те, що частинки середовища в заданий момент часу й на заданих відстанях від точки А знаходяться по різний бік від положення рівноваги й наближаються до нього.

Задача 3.2.

Хвилі від катера, що пливе озером, дістаються берега за час t = 0,5 хв і накочуються на нього з інтервалом часу $\tau=0,8$ с.

Визначити

відстань L від катера до берега, якщо відстань між гребенями хвиль l = 2 м.

Дано:

t = 30 c

l = 2 м

$\tau=0,8$ с

L - ?

Розв’язання

За час $\tau$ між послідовними ударами в берег хвиль від катера вони переміщуються на відстань l, отже, поширюються зі швидкістю

$v=\frac{l}{\tau}$ .

У такому разі відстань від катера до берега, яку хвилі долають за час t, становить

$L=vt=\frac{l}{\tau}t=\frac{2}{0,8}\cdot{30}= 75$ м.

Задача 3.3.

Визначити

швидкість поширення v монохроматичної хвилі з частотою $\nu=10$ Гц, якщо на промені в точках на відстані $\Delta{l}=100$ см одна від одної різниця фаз дорівнює $\Delta\varphi=\pi/4$ .

Дано:

$\nu=10$ Гц

$\Delta{l}=100$ см

$\Delta\varphi=\pi/4$

v – ?

Розв'язання

Відповідно до формули (3.9) можна записати:

$\Delta\varphi=\frac{2\pi}{\lambda}\Delta{l}$ ,

(1)

де $\Delta{l}$ – задана відстань між точками, $\lambda$ – довжина хвилі.

Швидкість поширення хвилі v виражається через довжину хвилі на основі формули (3.4a):

$v=\lambda\nu$ ,

(2)

Виразивши величину l з співвідношення (1) і підставивши її у формулу (2), дістанемо

$v=\frac{2\pi\nu\Delta{l}}{\Delta\varphi}= 80$ м/с.

Задача 3.4.

Відстань між гребенями хвиль на морі l = 5 м. Коли катер йде в напрямку поширення хвиль, вони б'ють у ніс катера з частотою n₁ = 2 удари за секунду. Якщо ж катер рухається назустріч, то удари йдуть з частотою n₂ = 4 удари за секунду.

Визначити

швидкість поширення хвиль v та швидкість катера V.

Дано:

l = 5 м

$n_{1}=2$

$n_{2}=4$

v, V - ?

Розв’язання

Відстань між гребенями l – це довжина хвилі, а кількість ударів об корпус дорівнює частоті коливань для рухомого спостерігача, що знаходиться на катері. Отже згідно з формулою (3.4a) можна записати:

	n₁l = v₁,	(1)
	N₂l = v₂,	(2)

де v₁, v₂ – швидкості поширення хвиль відносно катера у випадках руху вздовж та проти напрямку поширення хвиль. Згідно з законом додавання швидкостей (1.9)

v₁ = V – v;

v₂ = V + v,

де V, v – швидкості руху катера та поширення хвиль відносно води.

Підставивши сюди вирази (1), (2) для швидкостей і розв'язавши отриману систему, дістанемо відповіді:

$\left.\begin{align} {}n_{1}l=V-v \\ {}n_{2}l=V+v \\ \end{align}\right\}$ $\Rightarrow$ $\begin{align} {}V=l\frac{n_{1}+n_{2}}{2}=15\ {м/с}; \\ {}v=l\frac{n_{2}-n_{1}}{2}=5\ {м/с}. \\ \end{align}$

Задача 3.5.

Літак рухається на висоті H = 4 км з надзвуковою швидкістю .

Визначити

швидкість V літака, якщо спостерігач на землі почув його через $\tau= 10$ c після того, як побачив прямо над собою. Швидкість звуку v = 330 м/с.

Дано:

H = 4 км = 4000 м

$\tau= 10$ c

v = 330 м/с

V - ?

Розв’язання

При надзвуковій швидкості фронт звукової хвилі від літака має форму конуса з вершиною в місці його розташування і кутом між віссю та твірною, що визначається співвідношенням швидкостей звуку та літака (див. п. 1.2). На схематичному рисунку показано напрям руху літака OD та ділянки АВ і СD твірних фронту звукової хвилі на моменти, коли спостерігач з точи С побачив літак і почув його звук, відповідно. Тож, як видно, за час $\tau$ літак пролетів відстань BD рівну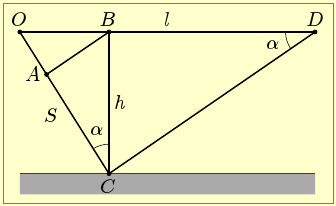 Рис. 15.5

$l=V\tau$ ,

а звук поширився на відстань AC, що складає

$s=v\tau$ .

Отже,

$V=\frac{l}{s}\cdot v$ (1)

Таким чином, задача зводиться до визначення відстані l, що легко зробити, врахувавши подібність трикутників ΔАВС і ΔВСD та теорему Піфагора. А саме,

$\frac{l}{s}=\frac{h}{\sqrt{{{h}^{2}}-{{\left( v\tau \right)}^{2}}}}=\frac{1}{\sqrt{1-{{\left( \frac{v\tau }{h} \right)}^{2}}}}$

Відтак із виразу (1) отримуємо відповідь:

$V=\frac{v}{\sqrt{1-{{\left( \frac{v\tau }{h} \right)}^{2}}}}$

Обчислення дають:

V ≈ 2100 км/год

Задача 3.6.

Із рухомого потяга подають звуковий сигнал з частотою $\nu_{0}=400$ Гц.

Визначити

швидкість V та напрям руху потяга, якщо людина, що вийшла на перон, почула сигнал потяга частотою $\nu=380$ Гц. Швидкість звуку v = 340 м/с.

Дано:

$\nu_{0}$ = 400Гц

$\nu$ = 380 Гц

v = 340 м/с

V – ?

Розв’язання

Приступаючи до розв'язання цієї та подібних задач, слід чітко усвідомити, що в теорії (п. 1.1) при визначенні рівняння та параметрів хвилі по замовчуванню приймається, що джерело і спостерігач є нерухомі відносно середовища, в якому поширюється хвиля. За таких умов частоти коливань, які сприймає спостерігач і створює джерело, збігаються, а швидкість їхнього поширення визначається тільки властивостями середовища і є табличною величиною. 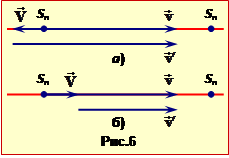Але коли джерело, спостерігач, або обоє рухаються, характеристики хвилі змінюються. Зокрема, для спостерігача на пероні (точка S_п на рис. 6) частота звукової хвилі $\nu$ буде відмінною від частоти $\nu_{0}$ коливань, які створює джерело звуку в рухомому електровозі (точка S_двиправити). Це можна пояснити наступним чином.

При нерухомих джерелі та спостерігачі частота хвилі задовольняє співвідношення (3.4a):

${{\nu }_{0}}=\frac{v}{{{\lambda }_{0}}}$ ,

(1)

в якому довжина хвилі ${{\lambda }_{0}}$ = vT₀ – то є відстань між її сусідніми "гребенями" (точками найбільшого стиснення, чи розрідження повітря), а T₀ = (1/ $\nu_{0})$ $v$ – час її проходження хвилею, який задається нерухомим джерелом. Але при рухомому джерелі вказана відстань ${{\lambda }}$ ≠ ${{\lambda }_{0}}$ . Дійсно, коли джерело рухається із швидкістю V, то на момент виходу з нього якогось гребеня хвилі попередній перемістився на відстань l₀ = vT₀, а джерело – на відстань l_д = VT₀ у тому, чи іншому напрямку. Тож відстань між гребенями дорівнє

= $\left( v\pm V \right)$ T₀,

де знак ''+'' відповідає віддаленню, а ''–'' зближенню електровоза та спостерігача. Отже, спостерігач чутиме звук із частотою

$\nu =\frac{v}{v\pm V}{{\nu }_{0}}$ ,

(2)

За умовою $\nu <{{\nu }_{0}}$ , отже в знаменнику виразу (2) має стояти знак ''+'':

$\nu =\left( \frac{v}{v+V} \right){{\nu }_{0}}$ ,

тобто електровоз віддаляється від пасажира.

Відтак із виразу (2) після елементарних викладок отримаємо наступну загальнувіповідь:

$V=\left( \frac{{{\nu }_{0}}}{\nu }-1 \right)v$ ,

і в числах

$V$ = 64,4 км/год.

Задача 3.7. Сигнальник на залізничному переїзді, повз який пройшов п отяг, подає звуковий сигнал частотою $\nu_{0}=500$ Гц.

Визначити

$V$ , якщо для машиніста частота сигналу складає ${{\nu }}$ = 470 Гц. Швидкість звуку v = 335 м/с.

Дано:

${{\nu }_{0}}$ = 500 Гц

${{\nu }}$ = 470 Гц

v = 335 м/с

$V$ – ?

Розв'язання

Ця задача є споріднена із попередньою, але відрізняється тим, що нерухомим є джерело (сигнальник), а не машиніст (спостерігач). За такої умови для обох довжина хвилі $\lambda$ (відстань, яку її гребені за час одного періоду ${{T}_{0}}=\left( 1/{{\nu }_{0}} \right)$ є однаковою й рівною (формула (3.4а)):

$\lambda =\frac{v}{{{\nu }_{0}}}$ . (1)

Але відносно машиніста гребені хвилі рухаються зі швидкістю не $v$ , ${v}'=v-V$ (див. [І], розділ І, ф-ла(1.10а)), і частота звуку для нього задовольняє співвідношення

$\lambda =\frac{v-V}{\nu }$ . (2)

Отож, прирівнявши праві частини виразів (1) і (2), після елементарних викладок дістанемо наступну загальну та числову вдповіді задачі:

$V=\left( 1-\frac{\nu }{{{\nu }_{0}}} \right)v$ = 72,4 км/год.

Задача 3.8. Два авто, котрі рухаються назустріч зі швидкостями ${{v}_{1}}$ = 90 км/год і ${{v}_{2}}$ = 60 км/год, подають звукові сигнали із частотою ${{\nu }_{10}}$ = 400 Гц і ${{\nu }_{20}}$ = 500 Гц, відповідно.

Визначити

частоту сигналу ${{\nu }_{I}}$ і ${{\nu }_{II}}$ , яку сприймає кожен водій при швидкості звуку ${{v}}$ = 340 м/с.

Дано:

${{v}_{1}}$ = 90 км/год

${{v}_{1}}$ = 60 км/год

${{\nu }_{10}}$ = 400 Гц

${{\nu }_{10}}$ = 500 Гц

${{v}}$ = 340 м/с

${{\nu }_{I}}$ – ?

${{\nu }_{II}}$ – ?

Розв'язання

Відповідно до умови, кожен водій є рухомим спостерігачем, який сприймає звук від рухомого джерела. Інакше кажучи, ця задача за змістом є об'єднанням двох попередніх. Отож, аби перший водій не рухався, то для нього у відповідності до формули (2) із задачі 3.6 частота сигналу складала би

${{\nu }^{*}}=\frac{v}{v-{{v}_{2}}}{{\nu }_{20}}$ .

Але через рух із швидкістю ${{v}_{1}}$ назустріч джерелу (другому автомобілю) вона, згідно з є більшою в $\left( v+{{v}_{1}} \right)/v$ разів і насправді дорівнює

${{\nu }_{I}}=\frac{v+{{v}_{1}}}{v-{{v}_{2}}}{{\nu }_{20}}$ .

Рух як такий є відносним, тож, помінявши у цьому виразі порядок індексів, отримаємо й другу відповідь:

${{\nu }_{II}}=\frac{v+{{v}_{2}}}{v-{{v}_{1}}}{{\nu }_{10}}$ .

Обчислення (не забудьте первести швидкості авто в {м/с}) дають:

${{\nu }_{I}}$ = 564 Гц; ${{\nu }_{II}}$ = 453 Гц.

На завершення варто зазначити, що розглянута в останніх прикладах варіативність частоти хвилі зумовлюється відносним рухом спостерігача та джерела і є притаманна також електромагнітним, зокрема, світловим хвилям. Вона називається ефектом Доплера по імені австрійського вченого, котрий її відкрив і пояснив. (Аби побачити один із проявів ефекту Доплера, клікніть тут)