ФІЗИКА. Вчимося розв'язувати задачі. "КОЛИВАННЯ ТА ХВИЛІ". Компенсаційний курс

Розділ ІІ. Електромагнітні коливання. Змінний струм

1.1. Вільні коливання у контурі

Вільні електричні коливання спостерігаються у коливальному контурі, причому в ідеальному контурі вони є гармонічними.

Повну інформацію про коливання містить диференціальне рівняння коливального контуру. Зокрема, з нього можна визначити частоту і період вільних коливань, одержати рівняння коливань заряду, напруги і сили струму в контурі.

У коливальному контурі відбуваються перетворення електричної і магнітної енергії коливань.

В електричному колі, що складається з конденсатора, котушки індуктивності та резистора, за який зазвчай правлять з'єднувальні провідники, за певних співвідношень між параметрами можуть виникати вільні електричні коливання. Тому таке коло називається коливальним контуром.

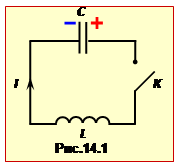У теорії електичних коливань базовою моделлю є ідеальний коливальний контур, який складається з ідеального конденсатора та ідеальної котушки індуктивності, котрі з'єднані провідниками, що не мають електричного опору (рис.14.1). Отже, в ідеальному контурі при протіканні струму немає втрат енергії, а електричне й магнітне поля повністю зосереджені всередині конденсатора та котушки, відповідно.

Електричні коливання в контурі виникають наступним чином. При замиканні ключа K конденсатор починає розряджатися, створюючи в котушці струм та зустрічну ЕРС самоіндукції ([ІІІ], ф-ла (3.15)). Тому струм встановлюється не одразу, а поступово і, досягнувши певної величини, так само поступово спадає. При цьому, через ЕРС самоіндукції, на момент розрядки конденсатора (q = 0, U = 0) струм у контурі не припиняється, тож конденсатор не розряджається, а перезаряджається до вихідної напруги. А далі все повторюється знову й знову, тож у контурі виникають незагасаючі вільні електричні коливання.

Описані процеси математично виражаються диференціальним рівнянням ідеального контуру, котре ґрунтується на тому, що в будь-який момент напруга на конденсаторі u збігається з ЕРС самоіндукції \({{\E}_{c}}\) в котушці:

\(u={{\E}_{c}}\).

Величини u і \({{\E}_{c}}\) визначаються формулами ([ІІІ], (2.23) і (3.14)), отже

\(\frac{q}{C}=-Li^{\prime}\),

(2.1)

де q – заряд конденсатора, \(i^{\prime}\) – похідна сили струму по часу.

Струм у контурі створюється перенесенням заряду з однієї обкладки конденсатора на іншу, тому миттєва сила струму i в контурі дорівнює швидкості зміни заряду конденсатора, котра визначається похідною заряду по часу:

\(i=q^{\prime}\).

(2.2)

Відповідно,

\(i^{\prime}=q^{\prime\prime}(t)\).

(2.3)

і, зробивши таку заміну у виразі (2.1), дістанемо диференціальне рівняння ідеального контуру:

\(q^{\prime\prime}=-\frac{1}{LC}q\),

(2.4)

котре за формою і загальним змістом є ідентичним із рівнянням (1.21). А це означає, що

вільні електричні коливання в ідеальному контурі є гармонічними

і відбуваються з циклічною частотою

\(\omega=\frac{1}{\sqrt{LC}}\).

(2.5)

Відповідно, їхній період визначається формулою Томсона:

\(T=2\pi\sqrt{LC}\),

(2.6)

а лінійна частота

\(\nu=\frac{1}{2\pi\sqrt{LC}}\).

(2.7)

Рівняння коливань заряду конденсатора в ідеальному контурі можна одержати з рівнянь механічних коливань заміною x → q. Зокрема, з рівняння (1.4) дістаємо:

\(q=q_{m}\cos(\omega{t}+\varphi_{0})\),

(2.8)

Напруга на конденсаторі \(u=q/C\) (розділ ІІ, (1.23)), тож рівняння коливань напруги на конденсаторі ідеального контуру має вигляд:

\(u=U_{m}\cos(\omega{t}+\varphi_{0})\),

(2.9)

де U_m – амплітуда напруги, що визначається як

\(U_{m}=\frac{q_{m}}{C}\).

(2.10)

Оскільки сила струму в контурі \(i=q^{\prime}(t)\), то сила струму в ідеальному контурі:

\(i=-\omega{q}_{m}\sin(\omega{t}+\varphi_{0})\)

(2.11)

\(i=I_{m}\cos\left(\omega{t}+\varphi_{0}+\frac{\pi}{2}\right)\),

(2.11a)

де амплітуда сили струму

\(I_{m}=\omega{q}_{m}\).

(2.12)

З рівнянь (2.9) і (2.11а) видно, що в ідеальному контурі коливання сили струму випереджають по фазі коливання напруги на конденсаторі на \(\pi/2\) або на чверть періоду (рис.14.2).

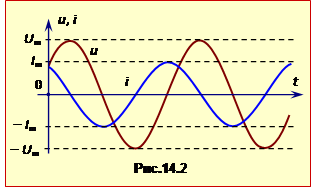
(Коливання заряду на конденсаторі завжди мають таку саму фазу, що й коливання напруги (див. рівняння (2.8) та (2.9)). Тому графік q(t) на рис.14.2 не показан0).

Енергія коливань в ідеальному контурі складається з енергії електричного поля конденсатора W_E та енергії магнітного поля котушки індуктивності W_B:

W = W_E + W_B.

(2.13)

Відповідно до формул ([III] (2.32а), (3.16)) і рівнянь (2.9), (2.11а)

	\(W_{Е}=\frac{q_{m}^{2}}{2C}\cos^{2}(\omega{t}+\varphi_{0})\) =\(\frac{q_{m}^{2}}{4C}\left(1+cos(2\omega{t}+2\varphi_{0})\right)\),	(2.14)
	\(W_{В}=\frac{LI_{m}^{2}}{2}\sin^{2}(\omega{t}+\varphi_{0})=\frac{LI_{m}^{2}}{2}\left(1-\cos(2\omega{t}+2\varphi_{0})\right)\).	(2.15)

З виразів (2.12) та (2.5) виходить:

\(LI_{m}^{2}=L\omega^{2}q_{m}^{2}\) \(\Rightarrow\) \(LI_{m}^{2}=\frac{q_{m}^{2}}{C}\).

Тому з виразів (2.13), (2.14) і (2.15) очевидно, що

\(W=\frac{q_{m}^{2}}{2C}=\frac{LI_{m}^{2}}{2}\) = const.

(2.16)

Таким чином,

повна енергія вільних коливань в ідеальному контурі зберігається, тобто не залежить від часу.

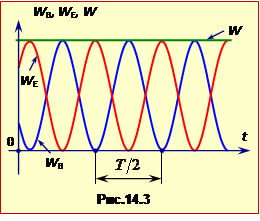На рис.14.3 показано графіки залежності від часу електричної W_E, магнітної W_B і повної енергії коливань W в ідеальному контурі.

Ці графіки наочно показують, що при вільних коливаннях в ідеальному контурі відбуваються неперервні взаємні перетворення електричного та магнітного полів без втрати енергії. Крім того, з рівнянь (2.14) і (2.15) випливає, що коливання енергії кожного з полів відбуваються з подвоєною частотою \(\omega^{\prime}\) відносно коливань напруги і струму:

\(\omega^{\prime}=2\omega\)

або

\(T^{\prime}=\frac{T}{2}\).

Порівняння формул (2.16) і (13.21) показує їх математичну ідентичність. При цьому для контуру величини (1/C) і L виконують ту ж саму роль, що й жорсткість пружини k та маса вантажу m у випадку пружинного маятника.