ФІЗИКА. Вчимося розв'язувати задачі. "ЕЛЕКТРИКА І МАГНЕТИЗМ". Компенсаційний курс
Розділ І. Електричне поле
Напруженість і потенціал
|
Задача 1.5. Електричне поле створюється двома однаково зарядженими малими кульками, що розміщені у вершинах правильного трикутника зі стороною a = 10 см. Визначити вектор напруженості поля \(\vec{E}\) в третій вершині, якщо в ній потенціал φ = 10 В. |
|
Задача 1.6. У вершинах правильного трикутника зі стороною a = 10 см закріплено точкові заряди q1 = 1нКл, q2 = –2q1 і q3 = –3 q1. Визначити напруженість \(\vec{E}_{0}\) електричного поля в центрі трикутника. |
|
Задача 1.7. Точкові заряди q і –q розташовано на осі OX на відстані 2l один від одного. Визначити та показати на графіку залежність Ex(x) проєкції напруженості електричного поля зарядів на лінії їхнього розташування. |
|
Задача 1.8. Електричне поле створюється металевою кулею радіуса R1 = 1 см із зарядом q = 1 нКл, до якої щільно прилягає сферичний шар діелектрика з проникністю \(\varepsilon=4,5\) і зовнішнім радіусом R2 = 2 см. Визначити та показати на графіках залежності напруженості E(r) і потенціалу φ(r) поля кулі від відстані r до її центра. |
|
Задача 1.9. Дві паралельні пластини із густиною заряду σ1 і σ2 закріплено перпендикулярно до осі ОХ у точках x = 0 і х = d (рис. 9). Уважаючи електричне поле системи однорідним, визначити та показати на графіку залежність від координати x: А) проєкції напруженості Ех(х); Б) потенціалу φ(х), прийнявши φ(0) = 0. Розглянути випадки: 1. σ1 = σ, σ2 = 2σ; 2. σ1 = σ, σ2 = – σ. Задача 1.10. По розміщеному в повітрі тонкому кільцю радіуса R рівномірно розподілено заряд q. Визначити: А) напруженість електричного поля Е на осі кільця в залежності від відстані r до його центра; Б) проаналізувати залежність Е(r) і показати загальний вигляд її графіка. Задача 1.11. Два однакові точкові заряди +q і –q, що закріплені на невеликій відстані l один від одного (рис. 11), утворюють "електричний диполь". Установити вираз залежності його потенціалу \(\varphi \left(r,\vartheta \right)\) в повітрі від відстані до центра r і кута (\vartheta \) за умови \(r\gg l\). |
Задача 1.5
Електричне поле створюється двома однаково зарядженими малими кульками, що розміщені у вершинах правильного трикутника зі стороною a = 10 см.
Визначити
напруженість поля\(\vec{E}_{1}\) в третій вершині, якщо в ній потенціал φ = 10 В.
|
Дано: l = 10 см = 0,1 м
φ = 10 В
|
|
E - ? |
Розв'язання
Відповідно до принципу суперпозиції (1.7), напруженість поля в вершині А трикутника (рис. 5) складає
\(\vec{E}=\vec{E}_{1}+\vec{E}_{2}\),
де \(\vec{E}_{1}\) і \(\vec{E}_{2}\) – вектори напруженості полів кожного із зарядів.
Модуль суми будь-яких двох векторів можна визначити за теоремою косинусів:
|
$E=\sqrt{E_{1}^{2}+E_{2}^{2}+2{{E}_{1}}{{E}_{2}}cos\alpha }$, |
|
де α – кут між додаваними векторами. При однакових зарядах кульок q1 = q2 = q та відстанях від них до т. А напруженості Е2 = Е1. Отже
| $E=2{{E}_{1}}\sqrt{2\left( 1+\cos \alpha \right)}=2{{E}_{1}}\cos \frac{\alpha }{2}$. | (1) |
Отриманий вираз є чинним при будь-якій відстані від зарядів до т. А та куті α. Але для рівностороннього трикутника α = 60°, тож
|
$E={{E}_{1}}\sqrt{3}$, |
(2) |
де напруженість поля одного заряду за формулою (1.6а) дорівнює
\(E_{1}=\frac{kq}{l^{2}}\).
Величину q не задано, але її легко виключити за допомогою формули (1.15а), позаяк потенціал поля однієї кульки φ1 складає половину заданого сумарного потенціалу φ:
$k\frac{q}{l}=\frac{\varphi }{2}$ $\Rightarrow $ ${{E}_{1}}=\frac{\varphi }{2l}$.
Відтак, підставивши це значення у вираз (2), отримаємо остаточну відповідь
$E=\frac{\varphi }{l}\cdot \frac{\sqrt{3}}{2}$ = 86,6 В/м.
Задача 1.6 У вершинах правильного трикутника зі стороною a = 10 см закріплено точкові заряди q1 = 1 нКл, q2 = –2q1 і q3 = –3q1.
Визначити
напруженість \(\vec{E}_{0}\) електричного поля в центрі трикутника.
|
Дано:
a = 10 см = 0,1 м
q1= 1 нКл = 10-9 Кл
q2= –2q1 = –2·10-9 Кл
q3= –3q1 = –3·10-9 Кл
|
| \(\vec{E}_{0}\) – ? |
Розв'язання
За принципом суперпозиції шуканий вектор
|
|
\(\vec{E}_{0}=\vec{E}_{1}+\vec{E}_{2}+\vec{E}_{3}\), |
(1) |
де \(\vec{E}_{1}\), \(\vec{E}_{2}\), \(\vec{E}_{3}\) – напруженості полів кожного із зарядів у точці O, рис. 6. Характеристиками шуканого вектора \(\vec{E}_{0}\) є його модуль Е та кут α, між ним і віссю ОХ. Для визначення цих величин оберемо систему вектора координат XOY, як показано на рис. 6, і запишемо рівняння (1) для проєкцій вектора \(\vec{E}_{0}\), враховуючи величину кутів між складовими векторами й осями та знаки проєкцій:
|
OX: \(E_{x}=(E_{1}+E_{2})\cos{30}^{\circ}\); OY: \(E_{y}=(E_{1}-E_{2})\sin{30}^{\circ}+E_{3}\). |
(2) |
 |
Звідси за допомогою формули (1.6а) можна визначити проєкції складових векторів і параметри результуючого вектора \(\vec{E}_{0}\). Але, враховуючи, що величини зарядів відносяться як (1 : 2 : 3) і відстань від них до т О \(r=a/2\cos{30}^{\circ}=a/\sqrt{3}\), рівняння (2) задля зручності спочатку варто записати у вигляді
Ex = 3ηcos30°;
Ey = η(3 – sin30°), де η =(3kq1/a2) = 2700 В/м,
і відтак обчислити проєкції Ex = 7015 В/м, Ey = 6750 В/м й остаточну відповідь:
\(E=\sqrt{E_{x}^{2}+E_{y}^{2}}=9735\) В/м;
\(\mathrm{tg}\alpha=\frac{E_{y}}{E_{x}}=0,962\) \(\Rightarrow \) \(\alpha=\) 43,9°.
Побудований за знайденими проєкціями вектор \(\vec{E}_{0}\) показано на рис. 6.
Задача 1.7
Точкові заряди q і –q розташовано на осі OX на відстані 2l один від одного.
Визначити та показати
на графіку залежність Ex(x) проєкції напруженості електричного поля зарядів на лінії їхнього розташування.
|
Дано: q, –q, l
|
|
Ex(x) – ?
|
Розв'язання
За принципом суперпозиції (1.7) у будь-якій точці напруженість поля системи \(\vec{E}\) дорівнює сумі напруженостей \(\vec{E}_{1}\), \(\vec{E}_{2}\) поля кожного із зарядів q1 = q і q2 = –q. Це стосується й проєкцій:
|
\(\vec{E}=\vec{E}_{1}+\vec{E}_{2}\) → Ех = Е1х + Е2х. |
(1) |
Зважаючи на співвідношення між модулями й напрямками (тож і знаками проєкцій) векторів складових і результуючого полів, лінія розташування зарядів (рис.7а) поділяється на три області А, В і С, із характерним для кожної співвідношенням між напрямками складових полів і величинами їхньої напруженості. Позаяк за умовою вектори \(\vec{E}_{1}\), \(\vec{E}_{2}\) і \(\vec{E}\) лежать на осі ОХ,
проєкції полів зарядів залежно від області складають Е1х = ± Е1 і Е2х = ± Е2, а для результуючого поля в кожній області визначаються виразами:
|
– Область А ( x < 0): Е1 > Е2 → Ех = – (Е1 – Е2) < 0. – Область В ( –l < x < l): Е1х, Е2х > 0 → Ех = Е1 + Е2 > 0. – Область С (x > l): Е1 < Е2, → Ех = – (Е2 – Е1) < 0. |
(2) |
При цьому в кожній точці з координатою х величини Е1 і Е2 визначаються відстанями r1 і r2 від неї до зарядів, які складають:
|
– Область А ( x < 0): r1 = |x| – l, r2 = |x| + l. – Область В ( –l < x < l): r1 = l – |x|, r2 = l + |x|, або r1 = l + |x|, r2 = l – |x|. – Область С (x > l): r1 = x + l r2 = x – l. |
(3) |
Відтак, підставивши записані вирази r1 і r2 у формулу (1.6а), знайдемо модулі E1 і E2, а потім за співвідношеннями (2) після перетворень отримаємо наступні вирази проєкцій Ex (x) для результуючого поля:
|
– Область А : $E=-4kql\frac{\left| x \right|}{\left( {{x}^{2}}-{{l}^{2}} \right)}$. – Область В : $E= 2kl\frac{{{x}^{2}}+{{l}^{2}}}{{{\left( {{x}^{2}}-{{l}^{2}} \right)}^{2}}}$. – Область С : $E=-4kql\frac{\left| x \right|}{\left( {{x}^{2}}-{{l}^{2}} \right)}$. |
(4) |
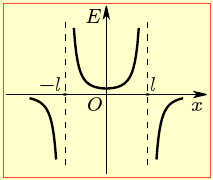
Далі слід було би побудувати за розрахунковими точками графік залежності Ex (x). Але його вигляд можна встановити й без розрахунків, опираючись на наступні міркування.
1. У кожній точці переважає поле заряду, що розташований ближче. Тож, як видно з рис.7а, в областях А і С проєкція результуючого поля Ех < 0, а в області В Ех > 0..
2. З тієї ж причини в усіх областях величина |Ех| зменшується при віддаленні від ближнього заряду.
3. За умовою |q2| = q1, тому графіки складових і результуючого полів є симетричним відносно осі ординат.
З урахуванням наведених міркувань графік Ex (x) виглядає, як показано на рис. 7б.
Задача 1.8.
Електричне поле створюється металевою кулею радіуса R1 = 1 см із зарядом q = 1 нКл, до якої щільно прилягає сферичний шар діелектрика з проникністю \(\varepsilon=4,5\) і зовнішнім радіусом R2 = 2 см.
Визначити та показати на графіках
залежності напруженості E(r) і потенціалу φ(r) поля кулі від відстані r до її центра.
|
Дано: R1 = 1 см = 0,01 м
R2 = 2 см = 0,02 м
q = 1 нКл = 10–9 Кл
\(\varepsilon=4,5\)
|
|
E(r) –?
\(\varphi(r)\) –?
|
Розв'язання
Для початку згадаємо деякі загальні відомості з теорії (п. 1.1).
1. Заряд q є рівномірно розподілений по поверхні кулі й створює електричне поле лише назовні.
2. Під дією поля кулі діелектрик поляризується: електрони в атомах трохи зміщуються в напрямі центра шару, й на його поверхнях з’являються поляризаційні (”зв’язані“) заряди однакової величини – q′ і +q′ (рис. 8). Ці заряди на додачу до поля зарядів кулі \(\vec{E}_{k}\) створюють зустрічне внутрішнє поле ${\vec{E}}'$, яке зменшує результуючу напруженість до величини (формула (1.6а))
${{E}}=\frac{{{{{E}}}_{k}}}{\varepsilon }$.
3. За умовою діелектрик є однорідним (ε = const) і в об’ємі лишається електрично нейтральним. Отож досліджуване електричне поле створюється двома рівномірно зарядженими концентричними сферами радіуса R1 і R2, які поділяють весь простір на три області: А (провідник, r < R1), В (діелектрик, R1 ≤ r < R2) і С (вільний простір, r ≥ R2), напруженість і потенціал поля в кожній з яких треба визначати окремо.

Напруженість Е(r)
Область А (r < R1). У провіднику електростатичне поле існувати не може, тож усередині кулі скрізь, включно з точками r = R1,
ЕА(r) = 0.
Область В (R1 ≤ r ≤ R2). У шарі діелектрика напруженість поля визначається формулою (1.6);
${{E}_{1B}}=\frac{q}{4\pi {{\varepsilon }_{0}}\varepsilon {{r}^{2}}}=\frac{kq}{\varepsilon {{r}^{2}}}$.
Відповідно, на поверхнях
${{E}_{1B}}=\frac{kq}{R_{1}^{2}}$ і ${{E}_{2B}}=\frac{kq}{R_{2}^{2}}$.
Область С (r ≥ R2). У цій області простору ε = 1, отже
${{E}_{С}}=\frac{kq}{{{r}^{2}}}$,
і в прилеглих до діелектрика точках
${{E}_{2C}}=\frac{kq}{R_{2}^{2}}$.
Таким чином, на графіку залежність Е(r) зображується відрізками квадратичних гіпербол, а на межах областей спостерігаються стрибки від Е1А = 0 до Е1B та від Е2В до Е2С, відповідно.
Потенціал φ(r)
Потенціал поля назовні рівномірно зарядженої сферичної поверхні, як і напруженість, збігається з такою для точкового заряду (формула (1.18)). Але позаяк потенціал визначається не напруженістю як такою, швидкістю її зміни, то відсутність поля (E(r) = 0) в якійсь частини польової зони означає не нульову величину, а сталість потенціалу (φ = const). Тому на графіку φ(r) не може бути стрибків (розривів).
Шукану залежність φ(r) будемо аналізувати в зворотньому порядку, рухаючися від віддаленої точки до центра кулі.
Область С (r ≥ R2). Ця область є вільна від діелектрика (для повітря ε = 1), отже за формулою (18а)
${{\varphi }_{C}}\left( r \right)=\frac{kq}{r}$,
і на прилеглій до діелектрика поверхні (r =R2)
${{\varphi }_{2}}=\frac{kq}{{{R}_{2}}}$.
Область В (R1 ≤ r ≤ R2). У діелектрику в напрямі до центра (при зменшенні r) потенціал продовжує зростати, починаючи з величини φ2. Тому φB = φ2 + ΔφВ, де ΔφВ – зміна потенціалу на шляху від т. 2 (зовнішня поверхня діелектрика) до довільної точки на відстані r від центра. Отже, згідно з формулою (1.18а),
${{\varphi }_{B}}={{\varphi }_{2}}+\frac{kq}{\varepsilon }\left( \frac{1}{r}-\frac{1}{{{R}_{2}}} \right)$,
і в т. 1 (r =R1)
\({{\varphi }_{1}}={{\varphi }_{2}}+\frac{kq}{\varepsilon }\left( \frac{1}{{{R}_{1}}}-\frac{1}{{{R}_{2}}} \right)\).
Область А (r < R1). Всередині кулі E = 0, і потенціал лишається сталим і складає
φА = φ1.
Далі належало би за за отриманими виразами та даними умови розрахувати таблиці значень і побудувати графіки залежностей E(r) і φ(r). Але в цьому немає потреби, бо їхній загальний вигляд є очевидним. А саме, області А вони зображуються горизонтальними відрізками, а в кожній з областей В і С – відрізками гіпербол. Тож для повного відображення картини поля достатньо за отриманими формулами обчислити його характеристики в точках 1 і 2:
Е1 = 0 і 20 кВ; Е2 = 5 кВ і 22,5 кВ;
φ1 = 550 В; φ2 =450 В.
Вигляд графіків залежностей E(r) і φ(r) показано на рис. 8-1.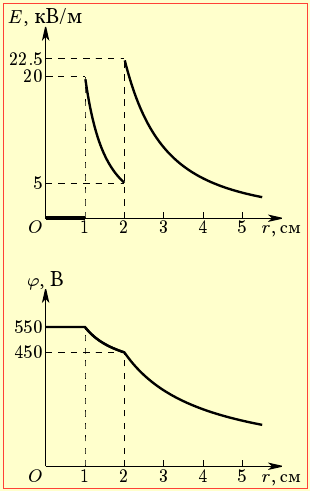 Рис. 8-1
Рис. 8-1
Задача 1.9
Дві паралельні пластини із густиною заряду σ1 і σ2 закріплено перпендикулярно до осі ОХ у точках x = 0 і х = d (рис. 9). Уважаючи електричне поле системи однорідним,
визначити та показати на графіку
залежність від координати x: А) проєкції напруженості Ех(х); Б) потенціалу φ(х), прийнявши φ(0) = 0. Розглянути випадки: 1. σ1 = σ, σ2 = 2σ; 2. σ1 = σ, σ2 = – σ.
|
Дано: d, σ
|
|
Ех(х) – ?
φ(x) – ?
|
Розв'язання
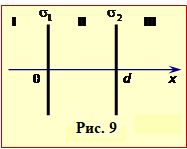
Заряджені пластини поділяють весь простір на три області: I, II, III (рис. 9), в яких за принципом суперпозиції (вирази (1.7), (1.15)) напруженість і потенціал електричного поля системи дорівнює сумі цих характеристик для поля кожної з пластин:
|
|
${{E}_{x}}={{E}_{1x}}+{{E}_{2x}}$ $\varphi ={{\varphi }_{1}}+{{\varphi }_{2}}$ |
(1) (2) |
При цьому напруженість визначаються заданою величиною σ (формула (1.9)), а потенціал – ще й вибором нульового рівня (п. 1.3). Тож надалі задля зручності введемо позначення (σ/2ε0) = E0 й за нульову точку потенціалу приймемо ліву пластину: φ(0) = 0.
Випадок 1.
А) У цьому випадку вектори \(\vec{E}_{1}\) і \(\vec{E}_{2}\), згідно з прийнятим позначенням і формулою (1.9), мають модулі Е1 = Е0, Е2 = 2Е0 і спрямовані, як на рис. 9-1а. Отже, для поля кожної пластини та системи в цілому маємо по областях:
|
І (х < 0) ІІ (0 < х < d) ІІІ (х > d) |
E1х = – Е0, Е2х = – 2Е0 $\Rightarrow$ ЕІх = – 3Е0 E1х = Е0, Е2х = – 2Е0 $\Rightarrow$ ЕІІх = –Е0 E1х = Е0, Е2х = 2Е0 $\Rightarrow$ ЕІІІх = 3Е0 |
(1A) |
${{E}_{x}}=-\frac{\varphi \left( x \right)}{x}$ $\Rightarrow$ $\varphi \left(x \right)=-\frac{{{E}_{x}}}{x}$
Аналогічно, прийнявши x1 = d, отримаємо для зони ІІІ:
${{E}_{x}}=-\frac{\varphi \left( x \right)-\varphi \left( d \right)}{x-d}$ $\Rightarrow$ $\varphi \left( x \right)=-{{E}_{x}}\left( x-d \right)+\varphi \left( d \right)$
Відтак, урахувавши дані таб. (1А), отримуємо наступні відповіді:
|
І (х < 0) ІІ (0 < х < d) ІІІ (х > d) |
$\varphi \left( x \right)= {{3E}_{0}}x$ $\varphi \left( x \right)= {{E}_{0}}x$ $\varphi \left( x \right)={{E}_{0}}\left( 4d-3x \right)$ |
(1Б) |
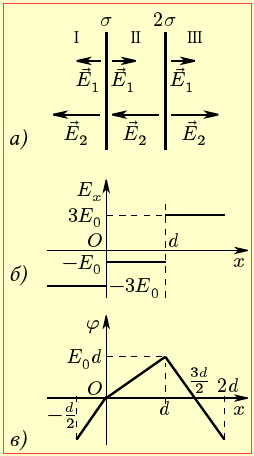
Таким чином, потенціал у напрямку осі ОХ в областях І, ІІ лінійно зростає, а в області ІІІ лінійно спадає. Відтак для побудови графіка (рис. 9-1в ) розрахуємо через величину E0 = (σ/2ε0) значення φ(x) у наступних точкахx
| х |
-d/3 |
0 |
d |
4d/3 |
5d/3 |
|
φ |
-E0d |
0 |
3E0d |
0 |
-E0d |
Випадок 2.
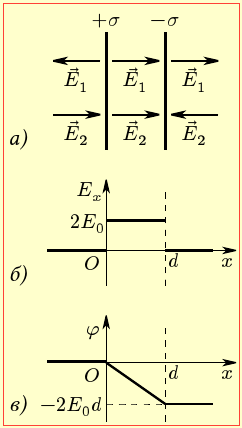
У цьому випадку \(\sigma_{1}\) = –\(\sigma_{2}\), і складові вектори \(\vec{E}_{1}\), \(\vec{E}_{2}\) мають однакові модулі та показані на рис. 9-2а напрямки.
Тож, згідно із співвідношенням (1), величина Ex в областях І, ІІІ дорівнює 0, а в області ІІІ складає 2Е0, як показано на рис. 9.2б. Відповідно, в області ІІ потенціал у напрямку осі OХ лінійно спадає від прийнятого значення φ(0) = 0 до φ(d) = –2Е0d, а поза нею лишається сталим (рис. 9.2в).
Варто зазначити, що цей випадок є характерним для плоского конденсатора, тож отриманий результат заслуговує на окрему увагу.
Задача 1.10.
По розміщеному в повітрі тонкому кільцю радіуса R рівномірно розподілено заряд q.
Визначити:
А) напруженість електричного поля Е на осі кільця в залежності від відстані r до його центра;
Б) проаналізувати залежність Е(r) і показати загальний вигляд її графіка.
|
Дано: R, q |
|
E(r) - ? |
Розв'язання
А). За принципом суперпозиції (1.7) напруженість $\vec{E}$ електричного поля кільця в будь-якій точці простору дорівнює сумі напруженостей полів його частин. Отож, подумки розділивши кільце на однакові малі ділянки й розклавши напруженість кожної на паралельну ${{\vec{E}}_ {i\parallel }}$ та перпендикулярну ${{\vec{E}}_{i\bot }}$ до осі кільця складову, можна записати
| $\vec{E}$ = $\sum{{{{\vec{E}}}_{i\parallel }}}$ + $\sum{{{{\vec{E}}}_{i\bot }}}$. | (1) |
У цьому виразі модулі та напрямки складових векторів визначаються формулою (1.6) через відстані та розташування заданої точки поля відносно всіх точок кільця. Тому розв'язати задачу в загальному вигляді (знайти формулу) для довільної точки не можна. Але на осі перпендикулярні складові полів діаметральних ділянок і всього кільця є компенсовані:
$\sum{{{{\vec{E}}}_{i\bot }}}$ = 0.
Тож, результуюча напруженість
$\vec{E}$ = $\sum{{{{\vec{E}}}_{i\parallel }}}$
є спрямована вздовж осі кільця й відповідно до формули (1.6) має модуль
$E=\sum{\left( \frac{\Delta {{q}_{i}}}{4\pi {{\varepsilon }_{0}}r_{i}^{2}}\cos {{\alpha }_{i}} \right)}$
Відтак, урахувавши, що за умовою відстані rі , отже й кути ${{\alpha }_{i}}$, є однакові й складають
${{r}_{i}}=\sqrt{{{r}^{2}}+{{R}^{2}}}$ і $\cos {{\alpha }_{i}}=\frac{r}{\sqrt{{{r}^{2}}+{{R}^{2}}}}$
отримаємо наступну відповідь:
| $E=\frac{qr}{4\pi {{\varepsilon }_{0}}\sqrt{{{\left( {{r}^{2}}+{{R}^{2}} \right)}^{3}}}}$ | (1) |
Б). Аби скласти наочне уявлення про характер залежності Е(r) на осі кільця, запишемо її наближені вирази поблизу ($r\ll R$) та далеко ($r\gg R$) від центра, де величиною r, або R можна нехтувати. А саме,
$r\ll R$ : $E\left( r \right)\approx \frac{qr}{4\pi {{\varepsilon }_{0}}{{R}^{3}}}$;
$r\gg R$ : $E\left( r \right)\approx \frac{q}{4\pi {{\varepsilon }_{0}}{{r}^{2}}}$
Із записаних виразів випливає, що при віддаленні від центра кільця напруженість поля спочатку лінійно, а потім уповільнено зростає так, що на певній відстані rm сягає максимуму і далі монотонно спадає, як показано на рис. 1.10-2.
З приводу отриманої залежності Е(r) (вираз ) варто зробити два зауваження.
1. Узявши та прирівнявши до нуля похідну Е′(r) від виразу (1), можна показати, що ${{r}_{m}}=\frac{R}{\sqrt{2}}$;
2. При $r\gg R$ значення Е(r) наближаються до величини напруженості поля точкового заряду (формула (1.6)). Це є цілком зрозумілим, позаяк кільце, як також і будь-які інші тіла, з великої відстані виглядають, як точкові.
Задача 1.11. Два однакові точкові заряди +q і –q, що закріплені на невеликій відстані l один від одного (рис. 11), утворюють "електричний диполь".
Установити
вираз залежності його потенціалу \(\varphi \left(r,\vartheta \right)\) в повітрі від відстані до центра r і кута (\vartheta \) за умови \(r\gg l\).
|
Дано: q, l, r, |
|
$\varphi (r,\vartheta )$ -? |
Розв'язання
Відповідно до принципу суперпозиції (вираз (1.15)) шуканий потенціал
$\varphi ={{\varphi }_{+}}+{{\varphi }_{-}}$
де φ+ і φ– – потенціали полів окремих зарядів ("полюсів") у повітрі визначаються формулою (1.16) при ε = 1, в якій через малість величини $l$ відстані до заданої точки до полюсів (див. рис. 11) складають \({{r}_{+}}=l-\Delta r\) і \({{r}_{-}}=l+\Delta r\), а \(\Delta r=\left( l/2 \right)\cos \vartheta\). Отже,
$\varphi =\frac{q}{4\pi {{\varepsilon }_{0}}}\left( \frac{1}{r-\left( l/2 \right)\cos \vartheta }-\frac{1}{r+\left( l/2 \right)\cos \vartheta } \right)$ $\Rightarrow $
$\varphi =\frac{ql\cos \vartheta }{{{r}^{2}}-{{\left( l/2 \right)}^{2}}{{\cos }^{2}}\vartheta }$
Позаяк за умовою \(r\gg{l}\), в записаному виразі величина ${{\left( l/2 \right)}^{2}}{{\cos }^{2}}\vartheta $ є неістотною, тож маємо наступну кінцеву віповідь:
\(\varphi =\frac{ql}{4\pi {{r}^{2}}}\cos \vartheta \) (\(r\gg l\))