ФІЗИКА. Вчимося розв'язувати задачі. "МОЛЕКУЛЯРНА ФІЗИКА І ТЕРМОДИНАМІКА". Компенсаційний курс

При розгляді поверхневого натягу в плівці рідини не слід забувати, що вона має дві поверхні й дві лінії дотику з твердим тілом. Це призводить до "подвоєння" сили поверхневого натягу, поверхневої енергії, роботи по зміні площі поверхні, тощо.

При обчисленні висоти підняття та ваги рідини в капілярі не враховувано  викривлення меніска й прийнято g = 10 м/с² .

Задача 3.7. Визначити точність  дозування мікстури за допомогою піпетки з діаметром отвору  d = 1 мм. Густина ліків \(\rho=1\) г/см³, поверхневий натяг \(\sigma=60\) мН/м.

Задача 3.8. Визначити  роботу A, необхідну для видування мильної бульби діаметром d = 10 см. Поверхневий натяг мильного розчину \(\sigma=40\) мН/м.

Задача 3.9. Дві вертикальні паралельні скляні пластини, розміщені на відстані d = 0,5 мм одна від одної, опустили на невелику глибину в посудину з водою. Визначити висоту підняття h води між пластинами відносно її рівня в посудині. Поверхневий натяг води \(\sigma\) = 74 мН/м, густина \(\rho\) = 1 г/м³.

Задача 3.10. Два легкі кубики з ребром a = 2 см із змочуваної речовини, один чистий, а інший змащений жиром, опустили на воду. Визначити  різницю глибин занурення кубиків \(\Delta{h}\). Поверхневий натяг води \(\sigma\) = 74 мН/м.

Задача 3.11. При вертикальному зануренні капілярної трубки діаметром d = 0,5 мм у посудину з водою (поверхневий натяг σ = 74 мН/м) вода піднялася на висоту h = 2,5 см над рівнем у посудині. Визначити радіус кривини R меніска (вільної поверхні води в капілярі).

++++++++++++++++++++++++++++++++

Задача 3.7

Визначити

точність дозування мікстури за допомогою піпетки з діаметром отвору d = 1 мм. Густина ліків \(\rho=1\) г/см³, поверхневий натяг \(\sigma=60\) мН/м.

Розв’язання

Точність дозуванні рідини піпеткою визначається об'ємом однієї краплі V₁, що відривається від носика піпетки (рис. 7). Відрив краплі настає, коли її вага зрівняється з силою поверхневого натягу F, яка діє по лінії дотику рідини з краєм отвору піпетки:

mg = F.

Сила поверхневого натягу, згідно з формулою (3.2),

\({F}=\sigma{l}=\sigma\pi{d}\),

а маса краплі \(m=\rho{V_{1}}\). Тож дістаємо наступну відповідь:

\(\rho{V_{1}}g=\pi{d}\sigma\)      \(\Rightarrow\)      \(V_{1}=\frac{\pi{d}\sigma}{\rho{g}}\) = 19 мм³.

Задача 3.8

Визначити

роботу A, необхідну для видування мильної бульби діаметром d = 10 см. Поверхневий натяг мильного розчину \(\sigma=40\) мН/м.

Розв’язання

При видуванні мильної бульби необхідно виконувати роботу проти сил поверхневого натягу. Згідно з формулою (3.3) для збільшення площі вільної поверхні рідини на величину \(\Delta{S}\) треба виконати роботу

\(A=\sigma\Delta{S}=\sigma(S_{2}-S_{1})\).

При видуванні бульби початкова площа поверхні S₁ = 0, а кінцева S₂ = 2S, де \(S=\pi{d^{2}}\) – площа поверхні сфери діаметром d. (Подвоєння у виразі S₂ спричинюється тим, що плівка має дві поверхні – зовнішню та внутрішню). Отже,

A = 2πd²σ= 2,5 мДж.

Задача 3.9

Дві вертикальні паралельні скляні пластини, розміщені на відстані d = 0,5 мм одна від одної, опустили на невелику глибину в посудину з водою (рис. 9).

Визначити

Визначити висоту підняття h води між пластинами відносно її рівня в посудині. Поверхневий натяг води \(\sigma\) = 74 мН/м, густина \(\rho\) = 1 г/м³.

Розв’язання

Пластини утворюють капіляр. Внаслідок змочування вода між пластинами буде підніматися, доки її вага mg не скомпенсує силу поверхневого натягу F, яка діє по лініях дотику води з внутрішніми поверхнями пластин (на рис. 9 ці лінії проходять через точки 1,2 перпендикулярно до площини рисунка). Отже, при рівновазі

Якщо позначити ширину пластини як l, то

а маса води в капілярі

\({m}=\rho{V}=\rho{dlh}\).

Підставивши ці вирази  умову рівноваги (1), дістанемо відповідь:

$ h=\frac{2\sigma }{\rho dg}$ = 3 см.

Задача 3.10

Два легкі кубики з ребром a = 2 см із змочуваної речовини, один чистий, а інший змащений жиром, опустили на воду. 

Визначити

різницю глибин занурення кубиків \(\Delta{h}\). Поверхневий натяг води \(\sigma\) = 74 мН/м.

Розв’язання

З умови зрозуміло, що один кубик (чистий) змочується, а інший (змащений) не змочується. Тому сили, що діють на воду на лінії дотику з кубиком, у першому випадку напрямлені вгору, а у другому – вниз. Відповідно, з боку води на кубики діють сили поверхневого натягу F_н, що напрямлені протилежно: для змоченого кубика вниз (рис. 10а), а для не змоченого – вгору (рис. 10б). Тому  чистий кубик буде занурений більше, ніж змащений.

Умови рівноваги кубиків мають вигляд:

Різницю глибин занурення \(\Delta{h}=h_{1}=h_{2}\) знайдемо, виразивши з системи (1) різницю значень архімедової сили:

\({F}_{A1}-F_{A2}=2F_{н}\).

Архімедова сила F_А1 = \(\rho(V_{1}-V_{2})\), а сила поверхневого натягу F_н = \(\sigma{l}\), отримаємо:

\(\rho(V_{1}-V_{2})g=2\sigma{l}\).

Різниця об'ємів зануреної частини кубиків дорівнює Δha², а довжина лінії дотику води до кубика l = 4a, отже

\(\rho\Delta{h}a^{2}g=2\sigma\cdot{4a}\)   \(\Rightarrow \)   \(\Delta{h}=\frac{8\sigma}{\rho{ag}}\) = 3 мм.

Задача 3.11. При вертикальному зануренні капілярної труби діаметром d = 0,5 мм у посудину з водою (густина ρ   = 1 г/см³, поверхневий натяг σ = 73 мН/м) вода піднялася на висоту h = 2,5 см над рівнем у посудині.

Визначити

радіус кривини R меніска (вільної поверхні води в капілярі).

Розв'язання

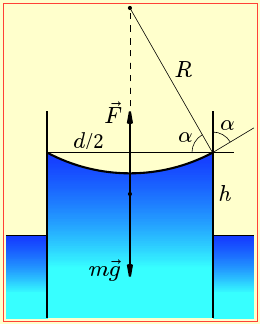
Поставлене в умові завдання означає, що радіус кривини меніска не збігається із радіусом трубки r = d/2, як це мало би бути при повному змочуванні  (п. 3.1). Про це свідчить і невідповідність заданій величині h, яка за формулою (3.10) мала складати

${h}'=\frac{4\sigma }{\rho gd}\approx 6\text{ см}\text{.}$

Це означає, що змочування трубки водою є неповним, і меніск є не півсферою з радіусом трубки, а сферичним сегментом із іншим радіусом кривини R і відповідним крайовим кутом α, рис. 11. Через це вага піднятої води mg = ρVg компенсується не всією силою поверхневого натягу F_н, а лишень її вертикальною складовою, величина котрої, згідно с формулою (3.7) і рис.11, складає

$F=\sigma l\cos \alpha $.

Отже,

$\rho Vg=\sigma l\cos \alpha $.

Звідси, врахувавши, що об'єм води в стовпчику $V=\pi {{r}^{2}}h, довжина контуру меніска \text{ }l=2\pi r\text{ i }\cos \alpha =\left( {r}/{R}\; \right)$, після спрощень отримаємо наступну відповідь:

$R=\frac{2\sigma }{\rho gh}$ = 0,6 мм,

що в 2,4 раза перевищує радіус трубки.

В отриманому результаті може здатися несподіваним те, що величина R не залежить від радіуса капіляра. Але в цьому немає нічого дивного, позаяк викривленість меніска залежить від ступеня змочування трубки водою, що визначається не розмірами, а фізичними властивостями  рідини та речовини трубки.