ФІЗИКА. Вчимося розв'язувати задачі. "МЕХАНІКА". Компенсаційний курс
Приклади розв'язування задач
Визначення роботи через силу
Задача 4.1. Брусок маси m повільно тягнуть горизонтальною поверхнею за мотузку, прикладаючи силу під кутом \( \alpha=45^{\circ}\) до горизонту. Визначити роботу A, яку при цьому виконують на шляху S = 6 м при коефіцієнті тертя між бруском і поверхнею \( \mu={0,5}\).
Задача 4.2. По дошці довжиною L, яка лежить на гладкій підлозі, з одного краю на інший пересувають брусок маси m і довжини l. Коефіцієнт тертя між тілами складає μ. Визначити сумарну роботу сили тертя за час пересування бруска.
Задача 4.3. Канат масою m = 6 кг і довжиною l = 5 м лежить на підлозі тренажерної зали з висотою стелі H = 6 м. Визначити роботу, яку треба виконати, аби підвісити канат до стелі.
| Задача 4.1 |
| Задача 4.1 |
Брусок маси m повільно тягнуть по горизонтальною поверхнею за мотузку, прикладаючи силу під кутом \( \alpha=45^{\circ}\) до горизонту.
Визначити
роботу A, яку при цьому виконують на шляху S = 6 м при коефіцієнті тертя між бруском і поверхнею \( \mu={0,5}\).
|
Дано: α = 45°
S = 6 м
μ = 0,5
|
|
A - ? |
Розв’язання
Сили, що діють на брусок, показано на рис. 1. За означенням (1) робота прикладеної до мотузки сили \( \vec{F}\) (рис.1) на шляху S дорівнює
| \( {A}=FS\cos\alpha \). | (1) |
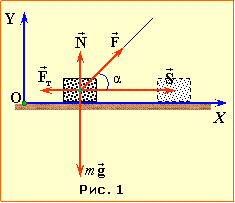 Позаяк брусок рухається без прискорення, рівнодійна сил \( \vec{F}\), тяжіння \( {m}\vec{g}\), нормальної реакції опори \( \vec{N}\) та тертя \( \vec{F}_{т}\) (рис. 4.1) дорівнює нулю:
Позаяк брусок рухається без прискорення, рівнодійна сил \( \vec{F}\), тяжіння \( {m}\vec{g}\), нормальної реакції опори \( \vec{N}\) та тертя \( \vec{F}_{т}\) (рис. 4.1) дорівнює нулю:
\( \vec{F}+\vec{F}_{т}+m\vec{g}+\vec{N}={0}\),
або в проекціях на осі координат
|
OX: \( {F}\cos\alpha-F_{т}={0}\), OY: \( {F}\sin\alpha+N-mg={0}\). |
Звідси, врахувавши, що \( {F}_{т}=\mu{N}\), дістанемо
\( {F}=\frac{\mu{mg}}{\cos\alpha+\mu\sin\alpha}\)
Відтак підставимо цей вираз у формулу (1) і знайдемо відповідь:
\( {A}=\frac{\mu{mg}S}{\cos\alpha+\mu\sin\alpha}\cdot\cos\alpha \) \( \Rightarrow \) \( {A}=\frac{\mu{mg}S}{1+\mu\mathrm{tg}\alpha}={19,6}\) Дж.
| Задача 4.2 |
| Задача 4.2 |
По дошці довжиною L, яка лежить на гладкій підлозі, з одного краю на інший пересувають брусок маси m і довжини l. Коефіцієнт тертя між тілами складає μ.
Визначити
сумарну роботу сили тертя за час пересування бруска.
|
Дано: m, l L μ |
|
А - ? |
Розв’язання
Між дошкою та бруском діють сили тертя \( \vec{F}_{1}\) = –\( \vec{F}_{2}\) (рис. 2) з модулем F = μmg, сумарна робота котрих
ККК
A = А1 + А2 = –μmgS1 + μmgS2 = –μmg( S1 – S2),
де S1 і S2 – модулі переміщення бруска і дошки відносно підлоги.
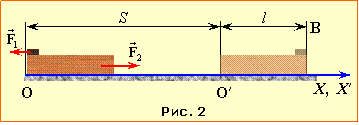
З рис. 2 видно, що ( S1 – S2) = (L – l), тож відповідь:
| A = – μmg(L – l). | (1) |
Ця задача є дуже простою й сама по собі не становить великого інтересу. Але, позаяк у системі сили взаємодії між парами тіл є незалежні, а самі сили є рівні за модулем і протилежні за напрямом (див. Розділ 2, п.п. 2.1, 2.2), отриманий результат відображує загальні властивості роботи сил тертя та опору:
1. Робота сили тертя, що діяла на дошку, А2 = μmgS2 > 0, проте повна робота А < 0. Це вказує на те, що
Повна робота внутрішніх сил тертя та опору в будь-якій системі завжди є від'ємна.
2. Величина (L – l) – це модуль переміщення ${{\vec{s}}_{12}}$ бруска відносно дошки та дошки відносно бруска ${{\vec{s}}_{21}}$ = – ${{\vec{s}}_{12}}$. Отже, в загальному вигляді відповідь (1) можна подати як
А = \( \vec{F}_{1}\)${{\vec{s}}_{12}}$ = \( \vec{F}_{2}\)${{\vec{s}}_{21}}$
і зробити наступний висновок:
сумарна робота сил тертя між двома тілами \( \vec{F}_{1}\) = –\( \vec{F}_{2}\) дорівнює добутку сили, що діє на одне з тіл на його переміщення відносно іншого.
Задача 4.3. Канат масою m = 6 кг і довжиною l = 5 м лежить на підлозі тренажерної зали висотою стелі H = 6 м.
роботу, яку треба виконати, аби підвісити канат до стелі.
|
Дано: |
|
А - ? |
Розв'язання
На початку підйому, доки переміщення кінця каната h є меншим за його довжину l, мінімальна потрібна сила F дорівнює вазі частини довжиною х, що звисає:
$F=\frac{mg}{l}h$,
а потім – вазі всього каната
F = mg.
Таким чином, маємо визначати роботу змінної сили, що найпростіше зробити, обчисливши площу під графіком сили рис. 3 (див. п. 4.1), тобто площу трапеції з основами H і (H – l) та висотою mg. Отже,
$A=\frac{1}{2}mg\left( 2H-l \right)$ = 210 Дж.