ФІЗИКА. Вчимося розв'язувати задачі. "МЕХАНІКА". Компенсаційний курс
2. Приклади розв'язування задач
2.1. Кінематичні величини, відносність руху
У всіх наведених задачах для прискорення вільного падіння прийнято значення g = 10 м/с2.
Задача 1.1. Автомобіль проїхав прямою дорогою відстань l1 = 1 км. Потім, рухаючись по дузі кола радіусом R = 300 м, розвернувся на 180° і, проїхавши далі прямо ще l2 = 200 м, зупинився. Загальний час руху склав t = 4 хв. Визначити за час руху: А) середню шляхову швидкість автомобіля; Б) модуль вектора середньої швидкості переміщення; В) кут між напрямом вектора переміщення та початковим напрямом руху.
Задача 1.2. На першій половині шляху автомобіль мав швидкість v1 = 36 км/год, а на другій – половину часу рухався зі швидкістю v2 = 72 км/год і стільки ж із швидкістю v3 = 90 км/год. Визначити середню швидкість автомобіля на всьому шляху.
Задача 1.3. Сліди дощових крапель на бічному склі трамвая є вертикальні під час руху і відхилені на кут α = 30° при зупинці. Визначити кут β, на який відхилені від вертикалі сліди дощових крапель на склі зустрічного трамвая, що рухається з такою самою швидкістю.
Задача 1.4. Хлопчик, який може плисти відносно води зі швидкістю u, що складає половину швидкості течії v, хоче переплисти річку. Визначити, під яким кутом α до берега хлопчик має тримати курс, аби його знесло течією якнайменше?
Задача 1.5. Визначити мінімальну швидкість umin, з якою має рухатись човен відносно води, аби потрапити з точки А на одному березі ріки у точку B на іншому. Швидкість течії V , ширина ріки h і відстань між точками А і В вздовж берега S є задані.
Задача 1.6. Від бакена, що стоїть посеред ріки, одночасно відпливають два човни: один за, а другий – поперек течії. Пройшовши однакову відстань, човни вертаються назад тими самими шляхами. Визначити відношення часів руху човнів τ1/τ2, якщо їхня швидкість відносно води в η = 1,8 разів перевищує швидкість течії.
Задача 1.7. Два катери, рухаючись річкою назустріч один одному, порівнялись і розійшлися під мостом. Відтак, розвернувшись через τ =0,5 год, вони знов зустрілися на відстані L = 2 км від мосту. Визначити швидкість течії V, якщо швидкості катерів відносно води лишалися незмінними.
Задача 1.8. Два автомобілі рухаються зі швидкостями v1 і v2 по двох взаємно перпендикулярних дорогах до перехрестя. Визначити, на якій найменшій відстані Lmin вони пройдуть один поз одного, якщо в початковий момент часу перебували на відстанях L1 і L2 від перехрестя.
Автомобіль проїхав прямою дорогою відстань L1 = 1 км. Потім, рухаючись по дузі кола радіусом R = 300 м, розвернувся на 180° і, проїхавши далі прямо ще L2 = 200 м, зупинився. Загальний час руху t = 4 хв.
Визначити за час руху:
А) середню шляхову швидкість автомобіля;
Б) модуль вектора середньої швидкості переміщення;
В) кут між напрямом вектора переміщення та початковим напрямом руху.
Розв'язання
|
Дано: L1 = 1 км
L2 = 200 м
R = 300 м
t = 4 хв
|
|
\( \langle{v}\rangle,\,\left|\langle\vec{v}\rangle\right|,\,\alpha \) - ? |
А) Пройдений автомобілем шлях (рис. 1) складається з довжин відрізків AC = L1 і EF = L2 та половини кола CDE:
S = L1 + πR + L2 = 2,14 км.
Тож середня шляхова швидкість (відношенню шляху до часу його проходження) дорівнює:
\( \langle{v}\rangle=\frac{S}{t}=\frac{2140}{240}\approx \) 8,9 м/с = 32,1 км/год.
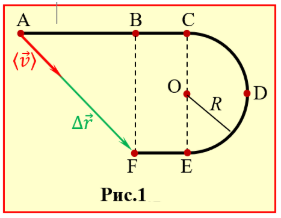 Б) Модуль середньої швидкості переміщення є відношенням модуля вектора переміщення до часу руху автомобіля:
Б) Модуль середньої швидкості переміщення є відношенням модуля вектора переміщення до часу руху автомобіля:
$\left| \left\langle {\vec{v}} \right\rangle \right|=\frac{\left| \Delta \vec{r} \right|}{\Delta t}$.
Із рис. 1 видно, що
$\left| \Delta \vec{r} \right|=\sqrt{{{\left( {{l}_{1}}-{{l}_{2}} \right)}^{2}}+{{\left( 2R \right)}^{2}}}$ = 1 км.
За умовою час руху t = (1/15) год, отже,
$\left| \Delta \vec{r} \right|$ = 15 км/год.
В) Напрям \( \left|\langle\vec{v}\rangle\right| \) збігається з напрямом \( \Delta\vec{r} \) і визначається кутом
$\alpha =\arcsin \left( \frac{2R}{\left| \Delta \vec{r} \right|} \right) $ ≈ 37°.
| Задача 1.2. |
На першій половині шляху автомобіль мав швидкість v1 = 36 км/год, а другу половину часу він рухався зі швидкостями v2 = 72 км/год і v3 = 90 км/год протягом двох рівних інтервалів.
Визначити
середню швидкість автомобіля на всьому шляху.
Розв'язання
|
Дано: v1 = 36 км/год
v2 = 72 км/год
v3 = 90 км/год
|
|
\( \langle{v}\rangle\) - ? |
Середня швидкість дорівнює відношенню пройденого шляху до часу, за який його подолано. Тож, позначивши як S половину всього шляху, t1 – час проходження першої половини шляху і τ – час руху на кожній з двох частин решти шляху, можемо записати:
| \(\left\langle v \right\rangle =\frac{2S}{{{t}_{1}}+2\tau }\). | (1) |
На всій дистанції автомобіль рухався із заданими сталими швидкостями, тож для кожної з двох половин шляху маємо:
$S={{v}_{1}}{{t}_{1}}$ $\Rightarrow $ ${{t}_{1}}=\frac{S}{{{v}_{1}}}$, $S={{v}_{2}}{{τ}}$ + ${{v}_{3}}{{τ}}$ $\Rightarrow $ $2\tau =\frac{2S}{{{v}_{2}}+{{v}_{3}}}$.
Відтак загальний час руху
${{t}_{1}}+2\tau $ = $\left( \frac{1}{{{v}_{1}}}+\frac{2}{{{v}_{2}}+{{v}_{3}}}\right)S$ = $\frac{2{{v}_{1}}+{{v}_{2}}+{{v}_{3}}}{2{{v}_{1}}\left( {{v}_{2}}+{{v}_{3}} \right)}S$,
і середня швидкість на всьому шляху
$\left\langle v \right\rangle =\frac{2v\left( {{v}_{2}}+{{v}_{3}} \right)}{2v+{{v}_{2}}+{{v}_{3}}}$ = 49,8 км/год.
На завершення, відмітимо, що середня швидкість автомобіля зовсім не дорівнює величині (v1 + v2 +v3)/3, як може здатися на перший погляд.
| Задача 1.3 |
 Сліди дощових крапель на бічному склі трамвая є вертикальні під час руху і відхилені на кут α = 30° при зупинці.
Сліди дощових крапель на бічному склі трамвая є вертикальні під час руху і відхилені на кут α = 30° при зупинці.
Визначити
кут \( \beta \), на який відхилені від вертикалі сліди дощових крапель на склі зустрічного трамвая, що рухається з такою самою швидкістю.
Розв'язання:
|
Дано: \( \alpha=30^{\circ} \) |
|
\( \beta \) - ? |
Вертикальні сліди вказують напрям швидкості крапель відносно трамвая, що рухається (рухома система відліку). Аналогічно, нахилені сліди вказують напрям швидкості крапель відносно нерухомого трамвая та землі (нерухома система відліку).
За законом додавання швидкостей (1.10) краплі відносно землі рухаються із швидкістю \( \vec{v} \), що в обох випадках дорівнює сумі їхніх швидкостей відносно трамвая \( \vec{u}\) та швидкості трамвая відносно землі \( \vec{V}\):
\( \vec{v}=\vec{u}_{1}+\vec{V}_{1}\),
\( \vec{v}=\vec{u}_{2}+\vec{V}_{2}\).
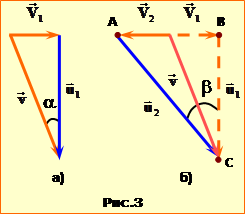
Із векторних діаграм цих рівнянь (рис. 3а,б) можна встановити зв'язок між напрямком руху крапель і величиною швидкості трамвая в обох випадках:
$\operatorname{tg}\beta =\frac{{{V}_{1}}+{{V}_{2}}}{{{u}_{1}}}$, $\operatorname{tg}\alpha =\frac{{{V}_{1}}}{{{u}_{1}}}$ .
Тож враховуючи умову V2 = V1 , маємо:
$\operatorname{tg}\beta =2\operatorname{tg}\alpha$.
Відтак, підставивши значення tgα, отримуємо відповідь:
$\operatorname{tg}\beta =\frac{2}{\sqrt{3}}$ $\Rightarrow $ β = 49,1°
| Задача 1.4 |
Хлопчик, який може відносно води плисти зі швидкістю u, що складає половину швидкості течії v, хоче переплисти річку.
Визначити,
під яким кутом \( \alpha \) до берега хлопчик має тримати курс, аби його знесло течією якнайменше?
Розв'язання
|
Дано: v/u = 2 |
|
α - ? |
Величина знесення хлопця L (рис. 4) залежить від ширини річки h та величини й напряму його швидкості \( \vec{v}\) відносно берега, котра визначається законом додавання швидкостей (1.10):
| \( \vec{v}=\vec{u}+\vec{V}\), | (1) |
де \( \vec{u}\) – швидкість руху хлопчика відносно води, \( \vec{V} \) – швидкість течії.
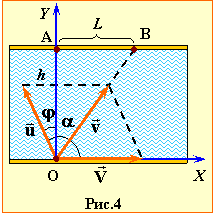 Аби встановити цю залежність, оберемо систему відліку, як на рис. 1.4. Тоді, коли хлопець тримає курс під кутом \( \varphi \) до осі OY, проєкції його швидкості \( \vec{v}\) на координатні осі складають:
Аби встановити цю залежність, оберемо систему відліку, як на рис. 1.4. Тоді, коли хлопець тримає курс під кутом \( \varphi \) до осі OY, проєкції його швидкості \( \vec{v}\) на координатні осі складають:
\( {v}_{x}=V-u\sin\varphi \),
\( v_{y}=u\cos\varphi \).
Час переправи визначається складовою швидкості \( {v}_{y}\) та шириною ріки h:
\( {t}=\frac{h}{v_{y}}=\frac{h}{u\cos\varphi}\).
За цей час хлопчик зноситься течією на відстань
| \( {L}({\varphi})=v_{x}t=h\cdot\frac{V-u\sin\varphi}{u\cos\varphi}\), | (2) |
За умовою задачі відстань L має бути якнайменшою. Але, при якому напрямку руху плавця так буде, безпосередньо з отриманого виразу не видно. Тому скористаємося методами математичного аналізу й дослідимо отриману функцію L(φ) на екстремум. Для цього спочатку знайдемо похідну L′(φ):
| \( {L}^{\prime}({\varphi})=\frac{h}{u}\cdot\frac{(-u\cos^{2}\varphi+(V-u\sin\varphi)\sin\varphi)}{\cos^{2}\varphi}\). | (3) |
Відтак згадаємо, що величина L(φ) буде мінімальною при значенні кута \(\varphi=\varphi_{m}\), для якого \( {L}^{\prime}({\varphi}_{m})\) дорівнює нулю. Отже, згідно з виразом (3),
\( {(V-u\sin\varphi_{m})\sin\varphi_{m}}-u\cos^{2}\varphi_{m}={0}\),
звідки
\( \sin\varphi_{m}=\frac{u}{V}=\frac{1}{2}\) \( \Rightarrow \) \( \varphi_{m}=30^{\circ}\).
Таким чином, необхідний кут між напрямком руху хлопця та напрямком течії дорівнює
\( \alpha=90^{\circ}+\varphi_{m}=120^{\circ}\).
| Задача 1.5 |
Визначити
мінімальну швидкість umin, з якою має рухатись човен відносно води, аби потрапити із заданої точки А на одному березі ріки в задану точку B на іншому. Швидкість течії V , ширина ріки h і відстань S між заданими точками відомі.
Розв'язання
|
Дано V, h, S |
|
umin - ? |
Цю задачу можна розв'язати аналогічно до попередньої, склавши рівняння для шуканої швидкості u і проаналізувавши його на мінімум. Але відповідь можна отримати значно простіше за допомогою геометричної побудови, показаної на рис. 5.
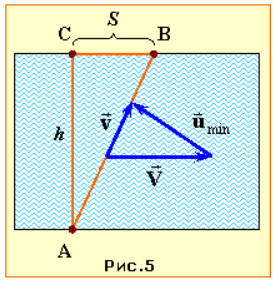 При переправі вектор швидкості човна \( \vec{v}\) відносно берега, що спрямовано по лінії AB, за законом додавання швидкостей (1.10) є пов'язаний із швидкістю човна відносно води \( \vec{u}\) та швидкістю течії \( \vec{V}\) співвідношенням
При переправі вектор швидкості човна \( \vec{v}\) відносно берега, що спрямовано по лінії AB, за законом додавання швидкостей (1.10) є пов'язаний із швидкістю човна відносно води \( \vec{u}\) та швидкістю течії \( \vec{V}\) співвідношенням
\( \vec{v}=\vec{u}+\vec{V}\).
Це відображає рис. 5, з якого очевидно, що швидкість човна відносно води буде мінімальною, коли вектор \( \vec{u}\) буде перпендикулярним до вектора \( \vec{v}\). В такому разі трикутник швидкостей є подібний до трикутника ABC, тож
\( \frac{u_{min}}{V}=\frac{h}{\sqrt{h^{2}+S^{2}}}\) \( \Rightarrow \) \( {u}_{min}=\frac{Vh}{\sqrt{h^{2}+S^{2}}}\).
| Задача 1.6 |
Від бакена, що стоїть посеред ріки, одночасно відпливають два човни: один за, а другий – поперек течії. Пройшовши однакову відстань, човни вертаються назад тими самими шляхами.
Визначити
відношення часів руху човнів \( \tau_{1}/\tau_{2}\), якщо їхня швидкість відносно води є в \( \eta{=1,8} \) раза більша за швидкість течії.
Розв'язання
|
Дано: η = 1,8 |
|
τ1/τ2 - ? |
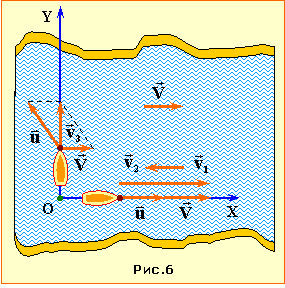
Позаяк за умовою швидкості човнів відносно води і пройдені ними відстані однакові, відміна у часах руху залежить тільки від швидкостей човнів відносно бакена.
Проаналізуємо їх, задля чого пов'яжемо систему відліку з бакеном (рис. 6) і приймемо що перший човен рухається вздовж осі ОХ. У такому разі модулі швидкості першого човна при русі вниз за течією v11 та вгору v12 дорівнюють
\( {v}_{11}={u+V}\) і \( {v}_{12}=u-{V}\),
де u – швидкість човна відносно води, V – швидкість течії. Відповідно до цього, якщо відстань в один кінець складає S, то повний час руху першого човна дорівнює
\( \tau_{1}=\frac{S}{V}\cdot\frac{2\eta}{\eta^{2}-1}\).
Аби рухатися перпендикулярно до берега, другий човен має правити під під певним кутом до осі OY, як показано на рис. 6. За такої умови швидкість човна відносно бакена в обох напрямках однакова і за теоремою Піфагора складає
\( {v}_{2}=\sqrt{u^{2}-V^{2}}=V\sqrt{\eta^{2}-1}\),
а час руху
| \( \tau_{2}=\frac{S}{V}\cdot\frac{2\eta}{\eta^{2}-1}\). | (2) |
Таким чином, відношення часів руху човнів дорівнює
\( \frac{\tau_{1}}{\tau_{2}}=\frac{\eta\cdot\sqrt{\eta^{2}-1}}{\eta^{2}-1}=\frac{\eta}{\sqrt{\eta^{2}-1}}={1,2} \).
| Задача 1.7 |
Два катери, рухаючись річкою назустріч один одному, порівнялися й розійшлись під мостом. Відтак, розвернувшись через τ =0,5 год, вони знов зустрілися на відстані L = 2 км від мосту.
Визначити
швидкість течії V, якщо швидкості катерів відносно води лишалися незмінними.
Розв'язання
|
Дано: L = 2 км
τ = 0,5 год
|
|
\( {V}\) - ? |
Цю задачу можна розв'язувати в нерухомій системі відліку, пов'язаній з берегом ріки (мостом), відносно якої сформульовані умова та завдання задачі. Для цього слід скласти рівняння руху катерів, врахувавши, що швидкість кожного з них при русі за течією становить u + V, а при русі проти дорівнює u – V (V – швидкість течії, u – швидкість катера відносно води). А далі треба розв'язати отриману систему рівнянь, врахувавши, що початкові та кінцеві положення катерів однакові.
Але задачу значно зручніше розглядати в рухомій системі відліку, пов'язаній з водою. Задля наочності приймемо, що під мостом в момент зустрічі катерів знаходиться ще й пліт, з яким і пов'яжемо рухому систему відліку. Позаяк ця система відліку рухається відносно берега зі швидкістю течії, то в ній швидкості катерів не залежать від напрямку руху і є однаковими. Тому катери віддаляються після першої зустрічі й повертаються до другої однаковий час, тож повний час їхнього руху між зустрічами t = 2τ. За цей час пліт, пливучи зi швидкістю V, проходить відстань L, тож швидкість течії дорівнює
\( {V}=\frac{L}{2\tau}\) = 2 км/год.
Як бачимо, при такому підходів задача практично є усною. Тож варто не забувати, що систему відліку, що мається на увазі в тексті задачі, не обов'язково, а інколи й недоцільно, використовувати для її розв'язування.
| Задача 1.8 |
 Два автомобілі рухаються зі швидкостями v1 і v2 по двох взаємно перпендикулярних дорогах у напрямку перехрестя.
Два автомобілі рухаються зі швидкостями v1 і v2 по двох взаємно перпендикулярних дорогах у напрямку перехрестя.
Визначити,
на якій найменшій відстані Lmin вони пройдуть один поз одного, якщо в початковий момент часу перебували на відстанях L1 і L2 від перехрестя.
|
Дано: v1, v2 L1, L2 |
|
Lmin - ?
|
Розв'язання
Розв'яжемо задачу теж у двох різних системах відліку.
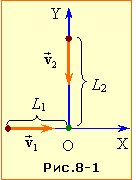
I спосіб. Розмістимо початок координат нерухомої системи відліку ХОY у перехресті і спрямуємо осі координат уздовж доріг (рис. 8-1). В такому разі початкові координати автомобілів x01 = – L1, y01 = 0, x02 = 0, y02 = L2, і рівняння руху автомобілів мають вигляд:
|
\( {x_{1}}=-L_{1}+v_{1}{t}\) \( {y}_{1}={0}\) |
\(x_{2}={0}\) \( {y}_{2}=L_{2}-v_{2}{t}\) |
(1) |
Тож відстань між автомобілями \( {L}=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}\) визначається виразом:
| L(t) = \(\sqrt{(v_{1}t-L_{1})^{2}+(L_{2}-v_{2}t)^{2}}\). | (2) |
Проаналізувавши отриману функцію L(t) на мінімум, отримаємо відповідь задачі. Для цього спочатку знайдемо похідну L′(t):
\( {L}^{\prime}(t)=\frac{2(v_{1}t-L_{1})v_1+2(L_{2}-v_{2}t)(-v_{2})}{2\sqrt{(v_{1}t-L_{1})^{2}+(L_{2}-v_{2}t)^{2}}}\) =
=\( \frac{\left( v_{1}^{2}+v_{2}^{2} \right)t-\left( {{L}_{1}}{{v}_{1}}+{{L}_{2}}{{v}_{2}} \right)}{\sqrt{{{\left( {{v}_{1}}t-{{L}_{1}} \right)}^{2}}+{{\left( {{L}_{2}}-{{v}_{2}}t \right)}^{2}}}} \).
У момент t0 розташування автомобілів на найменшій відстані, похідна L′(t0) = 0, отже,
\( \left(v_{1}^{2}+v_{2}^{2}\right)t_{0}-(L_{1}v_{1}+L_{2}x_{2})={0}\),
звідки
\( {t}_{0}=\frac{L_{1}v_{1}+L_{2}v_{2}}{v_{1}^{2}+v_{2}^{2}}\).
Підставивши це значення у вираз (2), знайдемо шукану відстань:
\( {{L}_{\min }}=\sqrt{{{\left( \frac{{{v}_{1}}{{\left( {{L}_{1}}{{v}_{1}}+{{L}_{2}}{{v}_{2}} \right)}^{2}}}{v_{1}^{2}+v_{2}^{2}}-{{L}_{1}} \right)}^{2}}+{{\left( {{L}_{2}}-\frac{{{v}_{2}}{{\left( {{L}_{1}}{{v}_{1}}+{{L}_{2}}{{v}_{2}} \right)}^{2}}}{v_{1}^{2}+v_{2}^{2}} \right)}^{2}}} \) =
=\( \frac{\left|L_{2}v_{2}-L_{1}x_{1}\right|}{\sqrt{v_{1}^{2}+v_{2}^{2}}}\).
II спосіб. Розв'яжемо тепер задачу в пов'язаній з першим автомобілем рухомій системі відліку X1O1Y1, швидкість якої відносно нерухомої системи ХОY складає \(\vec{V}=\vec{v}_{1}\). Тепер перший автомобіль весь час перебуває в початку відліку O1, а другий рухається відносно нього під певним кутом \( \alpha \) до осі O1X1 (рис. 8-2). Його швидкість \( \vec{u}\) за законом (1.11) дорівнює
| \( \vec{u}=\vec{v}_{2}-\vec{v}_{1}\), | (3) |
отже,
|
\( {u}=\sqrt{v_{1}^{2}+v_{2}^{2}}\). |
(4) |
|
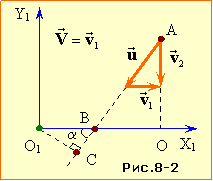
Із рис. 8-2 видно, що відстань L буде найменша, коли другий автомобіль знаходитиметься в т. С. Тому, якщо позначити довжину відрізка ВО як S, то
|
\({{L}_{\min }}=\left( {{L}_{1}}-S \right)\sin \alpha \). |
(5) |
Також є зрозуміло, що $S=\frac{{{L}_{2}}}{\operatorname{tg}\alpha }$, $\sin \alpha =\frac{{{v}_{2}}}{u}$ i $\operatorname{tg}\alpha =\frac{{{v}_{2}}}{{{v}_{1}}}$.
Відтак підставивши ці значення у вираз (5) і, замінивши величину u за формулою (4), отримаємо відповідь:
\( {L}_{min}=\left(L_{1}-\frac{L_{2}v_{1}}{v_{2}}\right)\frac{v_{2}}{u}=\frac{\left|L_{2}v_{1}-L_{1}v_{2}\right|}{\sqrt{v_{1}^{2}+v_{2}^{2}}}\).
Очевидно, що цей спосіб (використання рухомої системи відліку) робить розв'язок набагато коротшим.