ФІЗИКА. Вчимося розв'язувати задачі. "КОЛИВАННЯ ТА ХВИЛІ". Компенсаційний курс

Отримані вище результати є чинними не лише для механічних, ф й для інших хвиль. Тому в теорії величина $\xi \left( x,t \right)$ іменують хвильовою функцією, а її аргумент

– фазою.

Просторовий розподіл миттєвих значень хвильової функції наочно відображають за допомогою  

хвильових поверхонь: сукупностей точок, в яких фаза хвилі в даний момент часу має одне й те саме значення.

Форму хвильових поверхонь, яка залежить від конфігурації джерела та властивостей середовища, можна визначити, підставивши в рівняння фази  задану величину \(\varphi=\varphi_{0}\) та t = t₀. Зокрема, з рівнянь (3.8) плоскої та сферичної хвиль в однорідному середовищі виходить:

\(\varphi_{0}=\omega{t}-kx\)     \(\Rightarrow\)     x = const,

\(\varphi_{0}=\omega{t}-kr\)     \(\Rightarrow\)     r = const,

тобто, рівняння паралельних площин (рис.15.3а) і концентричних сфер (рис.15.3б), як і має бути. 

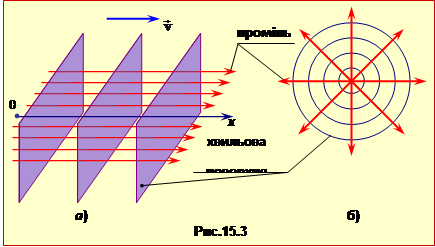
Окрім хвильових поверхонь, для візуального відображення хвилі також використовують

промені – лінії, вздовж яких енергія від джерела переноситься до різних точок.

Як видно з рис. 15.3, у плоских і сферичних хвилях промені є прямолінійні й скрізь спрямовані по нормалі (ортогонально) до хвильових поверхонь. Така взаємна орієнтація променів і хвильових поверхонь зберігається для хвиль будь-якого типу. Але це не стосується променів, які іншій конфігураці джерела та неоднорідності середовищі можуть бути викривлюватись.

Вище по замовчуванню вважалося, що хвиля займає весь простір. Насправді ж вона починається в місці розташування джерела й на будь-який визначений момент часу добігає точок, які утворюють фронт хвилі. Іншими словами,

фронт хвилі – то є поверхня, що розмежовує хвильову зону та область, куди хвиля ще не дійшла.

Зрозуміло, що, коли джерело перебуває в спокої, фронт хвилі збігається з крайньою хвильовою поверхнею. Але для рухомого джерела це не так. Для ілюстрації розглянемо розповсюдження хвилі від точкового джерела, котре прямолінійно рухається в однорідному середовищі із швидкістю u, що перевищує швидкість поширення хвилі v, прміром, як надзвуковий літак. За такої умови хвильова зона весь час знаходиться позаду джерела й починається в місці його розташування на даний момент (т. О на рис. 15.4).

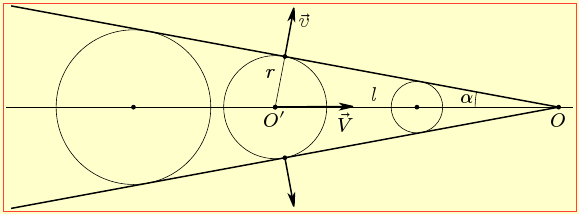
$l=u\tau $,

від джерела вже дійде до поверхні сфери радіуса

$r=v\tau $.

Отже, незалежно від положення т. ${O}'$,

$\frac{r}{v}=\sin \alpha =const$.

Це означає, що фронтом хвилі є бічна поверхня конуса, котра переміщується зі швидкістю хвилі в поперечному до твірної напрямі, розширюючи хвильову зону. Подібний ефект можна бачити, спостерігаючи слід на воді, який лишає за собою рухомий катер.

При русі джерела відносно спостерігача, крім фронту хвилі, змінюється і її частота. Це явище, котре  називається ефектом Доплера, детальніше розглянуто далі (п. 2. Приклади розв'язування задач, №№  1.6, 1.7).