physics.zfftt.kpi.ua

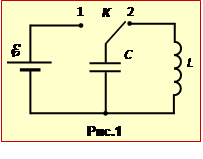
Задача 14.1. Конденсатор ємністю C = 1000 пФ зарядили від джерела ЕРС \(\mathcal{E}\) = 10 В (рис.1) і у момент часу t = 0 замкнули на котушку індуктивності L = 10 мкГн. Нехтуючи опором провідників, визначити: А) частоту коливань \(\nu\) в контурі; Б) залежність від часу:  – заряду конденсатора q(t);  – струму в контурі i(t);  – напруги u_L(t) на котушці.

Задача 14.2. До конденсатора C  ідеального контуру приєднали ще один такий же конденсатор. Визначити, у скільки разів (\(\eta\)) змінилася частота вільних коливань у контурі.

Задача 14.3. Коливальний контур з повітряним конденсатором має певну власну частоту (власною називається частота вільних коливань в ідеальному контурі). Контур помістили під вакуумний ковпак і відкачали повітря. В результаті власна частота контура змінилася на \(\Delta\nu=13\) Гц. Нехтуючи опором контура R, визначити діелектричну проникність \(\varepsilon\) повітря в умовах досліду.

 Задача 14.4. В ідеальному коливальному контурі ємність конденсатора C = 1 мкФ, індуктивність котушки L = 100 мкГн. При вільних коливаннях в контурі максимальний заряд конденсатора q_m = 1 мкКл. Визначити силу струму i  в контурі в момент, коли заряд конденсатора в k = 3 рази менший за максимальний.

Задача 14.5. У коливальному контурі ємність конденсатора C = 20 мкФ, індуктивність котушки L = 2 мГн. В деякий момент часу напруга на конденсаторі u = 10 В, а сила струму в котушці i₁ = 2 A. Визначити заряд конденсатора q в момент, коли сила струму в котушці i₂ = 1 A.

Задача 14.6. У коливальному контурі, що має котушку індуктивності L = 0,2 Гн, амплітуда сили струму I_m = 40 мА. Визначити енергію електричного W_E і магнітного W_B полів на момент, коли сила струму в n = 2 рази менша свого амплітудного значення.

Задача 14.7. У початковий момент часу напруга на конденсаторі контура має максимальне значення U₀ = 400 В. Ємність конденсатора C = 10 мкФ. Унаслідок наявності опору провідників, амплітуда вільних коливань в контурі поступово зменшується. Визначити кількість теплоти Q, що виділяється в контурі за час, протягом якого амплітуда напруги на конденсаторі зменшиться в n = 2 рази.

Задача 14.1

Конденсатор ємністю C = 1000 пФ зарядили від джерела ЕРС \(\mathcal{E}\) = 10 В (рис.1) і у момент часу t = 0 замкнули на котушку індуктивності L = 10 мкГн. Нехтуючи опором провідників,

визначити:
А) частоту коливань \(\nu\) в контурі;

Б) залежність від часу:

 – заряду конденсатора q(t);

 – струму в контурі i(t);

 – напруги u_L(t) на котушці.

Розв’язання

При замиканні зарядженого конденсатора C на котушку L (ключ K на рис.1 в положенні 2) утворюється коливальний контур, в якому виникають вільні коливання. Оскільки по умові R = 0, то контур ідеальний, і коливання в ньому є гармонічними.

Частота коливань визначається формулою (14.7):

При цьому циклічна частота \(\omega=2\pi\nu=10^{-7}\) c^-1. З умови задачі в початковий момент часу t = 0 напруга на конденсаторі, а значить і заряд, мають максимальні значення. Тому в рівнянні (14.8) початкову фазу слід узяти \(\varphi=0\). З урахуванням співвідношення (13.3), рівняння коливань заряду на конденсаторі має вигляд:

При підключенні до джерела на конденсаторі встановилася максимальна напруга U_m, що дорівнює ЕРС джерела \(U_{m}=\mathcal{E}\). Відповідно до формули (10.23), максимальний заряд

З урахуванням величини q_m і \(\nu\) (формула (1)), рівняння (2) в числовому вигляді записується як

Коливання сили струму в контурі визначаються загальним рівнянням (14.11). В даній задачі \(\varphi=0\), тому з урахуванням співвідношень (13.3):

Підставивши значення \(\nu\) (формула (1)) і q_m (формула (3)), отримаємо рівняння з числовими коефіцієнтами:

\(i(t)=-0,1\cdot\sin(10^{7}t)\), A.

Напруга на ідеальній котушці індуктивності (R = 0) виникає тільки завдяки явищу самоіндукції. Згідно співвідношенням (12.14), (14.25) і рівнянню (5), для будь-якого моменту часу

\(u_{L}(t)=-L(2\pi\nu)^{2}q_{m}\cos(2\pi\nu{t})\).

З урахуванням формули (14.7) і виразу (3) одержуємо:

\(u_{L}(t)=-\mathcal{E}\cos(2\pi\nu{t})=\mathcal{E}\cos(2\pi\nu{t}+\pi)\).

Це означає, що коливання напруги на котушці відбуваються в протифазі з коливаннями напруги на конденсаторі. В числовому вигляді рівняння (6) записується як

\(u_{L}=10\cdot\cos(10^{-7}t+\pi)\).

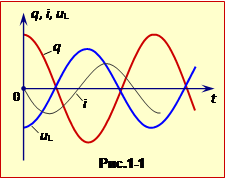
Графіки залежності від часу q(t), i(t) і u_L(t) показані на рис.1–1.

Задача 14.2

До конденсатора C  ідеального контуру приєднали ще один такий же конденсатор.

Визначити,
у скільки разів (\(\eta\)) змінилася частота вільних коливань у контурі.

Розв’язання

Відповідно до формули (14.5a), шукане відношення частот

де \(C,\ C^{\prime}\) – початкова і кінцева ємності контура.

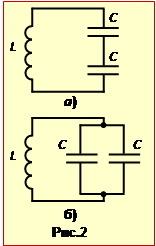Оскільки в умові не вказаний спосіб приєднання додаткового конденсатора, треба розглянути два випадки:

1) послідовне з'єднання (рис.2а),

2) паралельне з'єднання (рис.2б).

В першому випадку відповідно до формули (10.26), \(C^{\prime}=C/2\), а в другому, відповідно до формули (10.29), \(C^{\prime}=2C\).

Підставивши ці значення в співвідношення (1), отримаємо відповідь:

\(\eta_{1}=\sqrt{\frac{C}{(C/2)}}=\sqrt{2}\approx\) 1,41;

\(\eta_{2}=\sqrt{\frac{C}{(2C)}}=\frac{1}{\sqrt{2}}\approx\) 0,707.

Таким чином, при послідовному з'єднанні частота контура зростає в \(\sqrt{2}\approx\) 1,4 рази, а при паралельному – в стільки ж разів зменшується.

Задача 14.3

Коливальний контур з повітряним конденсатором має певну власну частоту (власною називається частота вільних коливань в ідеальному контурі). Контур помістили під вакуумний ковпак і відкачали повітря. В результаті власна частота контура змінилася на \(\Delta\nu=13\) Гц. Нехтуючи опором контура R,

визначити

діелектричну проникність \(\varepsilon\) повітря в умовах досліду.

Розв’язання

При відкачуванні з конденсатора віддаляється діелектрик (повітря) і зменшується його ємність (формула (10.24)). В результаті (формула (14.7)) збільшується власна частота контура. Отже, після відкачування власна частота контура:

де \(\nu_{0}\) - частота після відкачування. З формули (14.7):

де L – індуктивність контура, C₀ і C – ємність конденсатора після і до відкачування повітря.

Розділивши почленно вирази (2) і врахувавши співвідношення (1), отримаємо:

\(1+\frac{\Delta\nu}{\nu}=\frac{C}{C_{0}}\).

Звідси, використовуючи формулу (10.24), отримаємо відповідь:

\(\varepsilon=\left(1+\frac{\Delta\nu}{\nu}\right)^{2}\) = 1,00063.

Примітка. Існують прилади, які дозволяють виміряти власні частоти контурів з великою точністю. Тому описаний в задачі експеримент є одним з лабораторних способів вимірювання діелектричних проникність газів, які дуже мало відрізняються від одиниці.

Задача 14.4

В ідеальному коливальному контурі ємність конденсатора C = 1 мкФ, індуктивність котушки L = 100 мкГн. При вільних коливаннях в контурі максимальний заряд конденсатора q_m = 1 мкКл.

Визначити

силу струму i в контурі в момент, коли заряд конденсатора в k = 3 рази менший за максимальний.

Розв’язання

Задачу можна розв’язати двома способами.

I спосіб. Нехай заряд конденсатора змінюється з часом за законом

де q_m – амплітуда заряду, \(\omega\) – частота коливань, \(\varphi_{0}\) – початкова фаза. Згідно з рівнянням (14.11), сила струму в контурі

Щоб не визначати фазу для обумовленого в умові моменту часу, виразимо з формул (1) і (2) тригонометричні функції:

\(\cos(\omega{t}+\varphi_{0})=\frac{q}{q_{m}}\);    \(\sin(\omega{t}+\varphi_{0})=-\frac{i}{q_{m}\omega}\).

Якщо піднести ці вирази в квадрат і додати, отримаємо

\(\left(\frac{q}{q_{m}}\right)^{2}+\left(\frac{1}{q_{m}\omega}\right)^{2}=1\)    \(\Rightarrow\)    \(i=\omega\sqrt{1-\left(\frac{q}{q_{m}}\right)^{2}}\).

Враховуючи, що \(\frac{q}{q_{m}}=\frac{1}{k}\),  \(\omega=\frac{1}{\sqrt{LC}}\), з виразу (3) після перетворення знаходимо:

\(i=\frac{q_{m}}{k}\sqrt{\frac{k^{2}-1}{LC}}=\frac{10^{-6}}{3}\sqrt{\frac{9-1}{10^{-4}\cdot{10^{-6}}}}=0,094\) А = 94 мА.

II спосіб. Відповідь задачі можна отримати за допомогою закону збереження енергії.

В ідеальному контурі повна енергія W, яка дорівнює сумі енергій електричного W_E, і магнітного W_B полів, не зміниться:

W_E + W_B = const.

Повна енергія, згідно виразу (14.16), дорівнює максимальному значенню енергії електричного W_E або магнітного W_B полів:

\(W=\frac{q_{m}^{2}}{2C}=\frac{Li_{m}^{2}}{2}\).

Енергії W_E, і W_B  визначаються за формулами (14.14) і (14.15), тому

\(\frac{q^{2}}{2C}+\frac{Li^{2}}{2}=\frac{q_{m}^{2}}{2C}\)    \(\Rightarrow\)    \(i=\sqrt{\frac{q_{m}^{2}-q^{2}}{LC}}=\frac{q_{m}}{k}\sqrt{\frac{k^{2}-1}{LC}}\),

що, природно, співпадає з отриманим вище результатом. Зазначимо, що використовування закону збереження енергії істотно спростило розв’язування.

Задача 14.5

У коливальному контурі ємність конденсатора C = 20 мкФ, індуктивність котушки L = 2 мГн. В деякий момент часу напруга на конденсаторі u = 10 В, а сила струму в котушці i₁ = 2 A.

Визначити

заряд конденсатора q в момент, коли сила струму в котушці i₂ = 1 A.

Розв’язання

Для розв’язання задачі використаємо законом збереження енергії.

В ідеальному коливальному контурі повна енергія залишається незмінною: W = const. Ця енергія складається з енергій електричного і магнітного полів, отже, для будь-яких двох моментів часу t₁ і t₂ можна записати

Енергія електричного поля конденсатора і магнітного поля котушки виражається формулами (10.32) і (12.15) відповідно:

\(W_{E}=\frac{q^{2}}{2C}=\frac{Cu^{2}}{2}\);    \(W_{B}=\frac{Li^{2}}{2}\).

Підставивши ці формули у вираз (1), знайдемо

\(\frac{Cu^{2}}{2}+\frac{Li_{1}^{2}}{2}=\frac{q^{2}}{2C}+\frac{Li_{2}^{2}}{2}\)     \(\Rightarrow\)     \(q=\sqrt{C^{2}u^{2}+LC(Li_{1}^{2}-Li_{2}^{2})}\).

Виконаємо обчислення

\(q=\sqrt{4\cdot{10^{-10}}\cdot{10^{2}}+2\cdot{10^{-5}}\cdot{2}\cdot{10^{-3}}\cdot{(4-1)}}=4\cdot{10^{-4}}\) Кл = 400 мкКл.

Примітка. Цю задачу, як і попередню, можна розв'язати, розглядаючи рівняння коливань в конденсаторі. Але це набагато більш громіздкий спосіб.

Задача 14.6

У коливальному контурі, що має котушку індуктивності L = 0,2 Гн, амплітуда сили струму I_m = 40 мА.

Визначити

енергію електричного W_E і магнітного W_B полів на момент, коли сила струму в n = 2 рази менша свого амплітудного значення.

Розв’язання

Енергія магнітного поля котушки для будь-якого моменту часу визначається формулою (12.15)

\(W_{B}=\frac{Li^{2}}{2}\).

Звідси одержуємо значення повної енергії контура W (формула (14.16)) і енергії магнітного поля W_B на момент часу, коли I = I_m/2:

\(W=\frac{LI_{m}^{2}}{2}=\frac{0,2\cdot(4\cdot{10^{-2}})^{2}}{2}=1,6\cdot{10^{-4}}\) Дж = 160 мкДж.

\(W_{B}=\frac{LI_{m}^{2}}{2\cdot{4}}=\frac{W}{4}=40\) мкДж.

Енергію електричного поля W_E визначимо із співвідношення (14.13):

W_E = W – W_B = 120 мкДж.

Задача 14.7

У початковий момент часу напруга на конденсаторі контура має максимальне значення U₀ = 400 В. Ємність конденсатора C = 10 мкФ. Унаслідок наявності опору провідників, амплітуда вільних коливань в контурі поступово зменшується.

Визначити

кількість теплоти Q, що виділяється в контурі за час, протягом якого амплітуда напруги на конденсаторі зменшиться в n = 2 рази.

Розв’язання

Кількість теплоти, яка виділяється при протіканні струму по провідниках контура, дорівнює зменшенню енергії коливань:

Q = W₁ – W₂.

Відповідно до формул (14.16) і (10.32), енергія конденсатора

\(W=\frac{CU^{2}}{2}=\frac{q^{2}}{2C}\).

отже, записавши вирази енергій для заданих моментів часу, маємо

\(Q= \frac{CU_{0}^{2}}{2}-\frac{C(U_{0}/n)^{2}}{2}=\frac{CU_{0}^{2}}{2}\cdot\frac{n^{2}-1}{n^{2}}\)

Виконаємо обчислення:

\(Q=\frac{10^{-5}\cdot{400^{2}}}{2}\cdot\frac{4-1}{4}=0,6\) Дж.