ФІЗИКА. Вчимося розв'язувати задачі. "МЕХАНІКА". Компенсаційний курс
Приклади розв'язування задач
Визначення потужності та ККД
Задача 4.11. На ділянці траси з ухилом \(\alpha=5^{\circ}\) авто має швидкість v1 = 36 км/год на підйомі і v2 = 54 км/год – на спуску. Визначити швидкість авта v3 при русі горизонтальною ділянкою тієї самої траси, якщо двигун у всіх випадках розвиває однакову потужність.
Задача 4.12. Легкомоторний літак масою m = 1 т розганяється із сталим прискоренням до швидкості v = 30 м/с злітною смугою довжини S = 300 м . Визначити середню потужність \( \langle{P}\rangle \) двигуна літака на злеті, якщо коефіцієнт опору \( \mu={0,3}\).
Задача 4.13. Вантаж піднімають похилою площиною з кутом нахилу α до горизонту, прикладаючи силу вздовж площини. Визначити ККД η площини, якщо її коефіцієнт тертя із вантажем становить \( \mu \).
Задача 4.14. Вантаж маси M = 50 кг повільно підіймають за допомогою системи з рухомого та нерухомого блоків, прикладаючи силу до вільного кінця мотузки. Маса рухомого блока m = 5 кг. Визначити ККД \( \eta \) механізму. Маса мотузки та тертя в осях є неістотні.
На ділянці траси з ухилом \(\alpha=5^{\circ}\) авто має швидкість v1 = 36 км/год на підйомі і v2 = 54 км/год – на спуску.
Визначити
швидкість авта v3 при русі горизонтальною ділянкою тієї самої траси, якщо двигун у всіх випадках розвиває однакову потужність.
|
Дано: v1 = 36 км/год
v2 = 54 км/год
\( \alpha=5^{\circ}\)
|
|
v3 - ? |
Розв’язування
Відповідно до формули (4.16) шукана швидкість авта визначається, як
| \(v=\frac{P}{F}\), | (1) |
але потрібні для цього робоча потужність двигуна P і сила тяги F3 в умові задачі не вказано. Проте однаковість потужності двигуна в усіх випадках дозволяє знайти швидкість v3 через її порівняння із заданими величинами v1 і v2.
Авто в кожному випадку рухається із сталою швидкістю, тож сили тяги двигуна \( \vec{F}\), тяжіння \( {m}\vec{g}\), нормальної реакції дороги \( \vec{N}\) та опору \( \vec{F}_{оп}\) (рис. 4.11) є компенсовані:
| \( \vec{F}+\vec{N}+m\vec{g}+\vec{F}_{оп}={0}\). | (2) | |
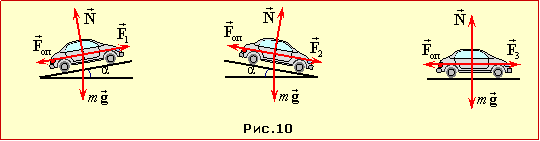 |
Запишемо умову (2) в проєкціях на напрям руху авто для кожного випадку. При цьому, взявши до уваги малість кута α, покладемо cosα = 1 i sinα = α(рад). Тоді N = mg, проєкція \( {m}\vec{g}\) на напрям руху на похилій ділянці складає mgα, тож умови (2) набувають вигляду:
| \( {F}_{1}-mg\alpha-F_{оп}={0}\), | (3) | |
| \( {F}_{2}+mg\alpha-F_{оп}={0}\), | (4) | |
| \( {F}_{3}-F_{оп}={0}\) |
(5) |
Далі додавши рівняння (3) та (4) і врахувавши, що згідно з (5) Fоп = F3, отримаємо співвідношення між силами тяги двигуна:
F1 + F2 – 2F3 = 0 \( \Rightarrow \) F1 + F2 = 2F3.
Нарешті, виразивши в отриманому рівнянні сили через відношення потужності до швидкості, дістанемо відповідь:
\( \frac{P}{v}_{1}+\frac{P}{v_{2}}=2\frac{P}{v}_{3}\) \( \Rightarrow \) \( \frac{1}{v_{1}}+\frac{1}{v_{2}}=\frac{2}{v_{3}}\) \( \Rightarrow \) \( {v}_{3}=\frac{2v_{1}v_{2}}{v_{1}+v_{2}}\).
Обчислення дають
v3 = 43 км/год.
Легкомоторний літак масою m = 1 т розганяється із сталим прискоренням до швидкості v = 30 м/с злітною смугою довжини S = 300 м .
Визначити
середню потужність \( \langle{P}\rangle \) двигуна літака на злеті, якщо коефіцієнт опору \( \mu={0,3}\).
|
Дано: m = 1 т
S = 300 м
v = 30 м/с
\( \mu=0,3 \)
|
|
\( \langle{P}\rangle\) - ? |
Розв’язування
Середня потужність дорівнює відношенню зробленої роботи до часу її виконання:
| \( \langle{P}\rangle=\frac{A}{t}\). | (1) |
Згідно з виразом (4.4), кінетична енергія, отримана літаком за час розгону, дорівнює сумі роботи двигуна А та роботи сил опору Аоп. Отже,
A = Wк – Aоп = \(\frac{mv^{2}}{2}\) + μmgS,
де враховано вираз сили опору та те, що Aоп < 0.
Час розгону визначимо через відстань S та кінцеву швидкість v з рівнянь кінематики (1.16):
\( \left. \begin{matrix} S=\frac{a{{t}^{2}}}{2} \\ v=at \\\end{matrix} \right\}\ \ \ \ \ \Rightarrow \ \ \ \ \ \frac{S}{v}=\frac{t}{2}\ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ t=\frac{2S}{v}\).
Підставивши отримані вирази А та t у формулу (1), знайдемо відповідь:
\( \langle{P}\rangle=\frac{mv}{2}\left(\frac{v^{2}}{2S}+\mu{g}\right)={66,6}\) кВт.
Вантаж піднімають похилою площиною з кутом нахилу α до горизонту (рис. 4.13), прикладаючи силу вздовж площини.
Визначити
ККД η похилої площини, якщо її коефіцієнт тертя із вантажем становить μ.
|
Дано: \( \alpha\)
\( \mu \)
|
|
\( \eta \) - ? |
Розв’язування
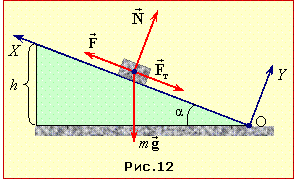
ККД похилої площини дорівнює відношенню потенціальної енергії піднятого вантажу W до роботи А прикладеної сили \( \vec{F}\), рис. 4.13:
| η = \(\frac{W}{A}\) = \(\frac{mgh}{FS}\). | (1) |
де m – маса вантажу, h – висота підйому, S – пройдений шлях.
Сила F долає "скочувальну" складову сили тяжіння mg·sinα та силу тертя Fт = μN = μmg·cosα і має величину
F = mg·sinα + μmg·cosα = mg(sinα + μcosα).
Шлях вантажу
|
$S=\frac{h}{\sin \alpha }$ |
Підставивши значення F i S у вираз (1), після елементарних перетворень отримаємо наступну відповідь:
$\eta =\frac{1}{1+\operatorname{ctg}\alpha }$.
Вантаж маси M = 50 кг повільно підіймають за допомогою системи з рухомого та нерухомого блоків (рис. 4.14), прикладаючи певну силу до вільного кінця мотузки. Маса рухомого блока m = 5 кг.
Визначити
ККД \( \eta \) механізму.
|
Дано: M = 50 кг
m = 5 кг
|
|
\( \eta \) -? |
Розв’язування
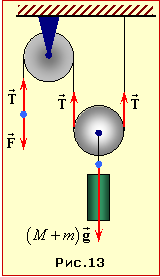 Рухомий блок і вантаж можна розглядати як одне тіло маси (M+m), на яке діють сила тяжіння \( {(M+m)}\vec{g}\) та дві сили натягу мотузки \( \vec{T}\), рис. 4.14.
Рухомий блок і вантаж можна розглядати як одне тіло маси (M+m), на яке діють сила тяжіння \( {(M+m)}\vec{g}\) та дві сили натягу мотузки \( \vec{T}\), рис. 4.14.
Вантаж піднімають повільно, тож сили є зрівноважені:
(M +m)g = 2T.
Так само зрівноважені є й прикладена сила та сила натягу мотузки: T = F. Отже,
\( {(M+m)}g={2F}\) \( \Rightarrow \) \( {F}=\frac{(M+m)g}{2}\).
Цей результат ілюструє функціональне призначення блокових механізмів – піднімання вантажів силою, меншою за їхню вагу.
При піднятті вантажу разом із блоком на висоту h кінець мотузки переміщується на відстань \( {l}={2h}\), і робота сили F (затрачена робота)
\( {A}=Fl=\frac{(M+m)g}{2}\cdot{2h}=(M+m){gh}\).
Але корисною є робота тільки по підйому вантажу \( {A}_{к}=Mgh \), тож ККД цієї системи блоків дорівнює:
\( \eta=\frac{A_{к}}{A}=\frac{M}{M+m}\) = 91 %.
Зауважимо, що задачу можна розв’язати і без прямого визначення роботи, використовуючи зв’язок між нею та механічною енергією. Справді, затрачена робота дорівнює зміні потенціальної енергії всієї системи, тоді як корисна — тільки вантажу. Отже,
\( {A}=(M+m)gh \), \( {A}_{к}={Mgh}\),
і
\( \eta=\frac{A_{к}}{A}=\frac{Mgh}{(M+m)gh}=\frac{M}{M+m}\),
що, природньо, збігається з отриманим раніше результатом.