ФІЗИКА. Вчимося розв'язувати задачі. "СУЧАСНА ФІЗИКА". Компенсаційний курс
Розділ 21. Атомне ядро
21.2. Енергія зв'язку атомного ядра
|
Нуклони в ядрі утримуються специфічними ядерними силами. Міцність ядра характеризується енергією зв'язку атомного ядра, яку можна визначити за відповідними формулами розрахунку енергії зв'язку. Зчеплення між нуклонами характеризується питомою енергією зв'язку нуклонів. |
|
Ядерні сили є проявом так званої сильної взаємодії. Сильна взаємодія – це фундаментальна взаємодія, тобто вона не зводиться ні до яким іншої. Ядерні сили мають різноманітні і складні властивості. Вкажемо тільки на деякі з них: 1. Ядерні сили є "найсильнішими" з усіх відомих сил. Зокрема, сили ядерного зчеплення між нуклонами в ядрі набагато переважають сили електричного відштовхування між протонами. 2. Ядерні сили є "зарядосиметричними" - вони не залежать від наявності або відсутності у частинок електричного заряду. 3. Ядерні сили є короткодіючими. Вони виявляються тільки на відстанях \(r\le{10}^{-15}\) м, тобто діють лише всередині атомного ядра. 4. Ядерні сили мають властивість насичення. Це означає, що кожен нуклон у ядрі може взаємодіяти тільки з обмеженою кількістю інших нуклонів. Останні дві властивості ядерних сил принципово відмінні від електромагнітних. Електромагнітні сили є дальнодіючими і не насичуються. Це означає, що у системі електрично заряджених частинок кожна з них взаємодіє з усіма іншими незалежно від кількості частинок і розмірів системи. |
|
З виразів (21.5) і (21.4) легко одержати розрахункові формули для енергії зв'язку ядра. Очевидно, що сумарна маса нуклонів, що входять у задане ядро
де Z – зарядове число ядра (кількість протонів), A – масове число (загальна кількість нуклонів), mp і mn – маси вільних протона і нейтрона. З урахуванням виразів (21.5) і (21.6) формула (21.4) набуває вигляду
У довідкових таблицях наводяться не маси ядер, а маси нейтральних атомів. Тому замість формули (21.7) використовують модифіковану формулу
де \(m_{н}\) – маса нейтрального атома Гідрогену \({}_{1}^{1}\mathrm{H}\) – маса нейтрального атома розглянутого ізотопу. У ядерній фізиці масу визначають в а.о.м (1 а.о.м. = 1,66\(\cdot{10}^{-27}\) кг), а енергію – в мегаелектронвольтах (МеВ) (1 МеВ = 106 еВ = \(1,6\cdot{10}^{-13}\) Дж). При цьому масі m1 = 1 а.о.м. відповідає енергія (енергетичний еквівалент) \(E_{1}=m_{1}c^{2}=931,5\) МеВ. Тому для практичних розрахунків замість формули (21.7а) зручно використовувати числову формулу
в якій маси виражені в а.о.м. |
|
Зчеплення (зв'язок) окремого нуклона з усіма іншими нуклонами в ядрі характеризується усередненою величиною, що називається питомою енергією зв'язку нуклонів. Питома енергія зв'язку нуклонів \(E_{пит}\) – це відношення енергії зв'язку ядра \(E_{зв}\) до загальної кількості нуклонів A:
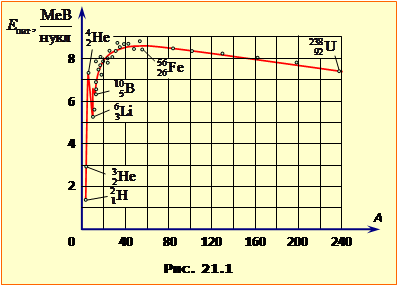
Величина Eпит складно залежить від багатьох факторів і не може бути виражена формулою, але існує чітка закономірність, показана умовним графіком на рис.21.1 (графік є умовним у тому сенсі, що масові числа ядер не формують безперервну послідовність). При збільшенні кількості нуклонів у ядрі A питома енергія \(E_{пит}\) спочатку різко зростає, досягаючи максимуму 8,8 МеВ/нукл при \(A=40\sim{50}\), а потім повільно монотонно спадає до \(\approx{7,6}\) Мев/нукл для нуклідів, розташованих у кінці періодичної системи (\(A=240\sim{250}\)).
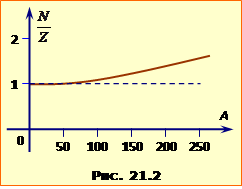
Зростання \(E_{пит}\) на початковій ділянці пояснюється збільшенням кількості партнерів, з якими взаємодіє кожен нуклон у ядрі. Подальший хід залежності \(E_{пит}(A)\) пов'язаний із властивістю насичення ядерних сил. При значенні \(A\approx{40}\) кожний нуклон у ядрі вже має максимально можливу кількість партнерів, з якими може взаємодіяти. Тому подальше збільшення A ніяк не впливає на питому енергію ядерної взаємодії нуклонів. Однак між протонами діють сили електричного відштовхування, які послаблюють зчеплення між протонами і, відповідно, зменшують питому енергію зв'язку. Для електричних сил ефект насичення відсутній, тому зменшення питомої енергії зв'язку спостерігається до самого кінця періодичної системи. З цим же зв'язана і закономірна зміна співвідношення між кількістю нейтронів N і кількістю протонів Z при збільшенні загальної кількості нуклонів A, що показано умовним графіком на рис.21.2.
Відношення N/Z поступово збільшується від значення 1, типового для легких нуклідів, до значення 1,6 наприкінці періодичної системи. Ядра поступово нібито "розбавляються" нейтронами. Це призводить до збільшення відстані між протонами та послабленню електричного відштовхування між ними, а отже, й до підвищення міцності ядра. |