ФІЗИКА. Вчимося розв'язувати задачі. "СУЧАСНА ФІЗИКА". Компенсаційний курс
Розділ 20. Будова атома
Приклади розв'язування задач
При розв'язуванні задач на атом Гідрогену треба врахувати наступне.
|
1) |
Якщо електрон перебуває у збудженому стані, то він може перейти на будь-який з більш низьких енергетичних рівнів. Якщо такий рівень не є першим (\(n\ne{1}\)), то електрон і надалі може переходити на нижчі рівні. Як наслідок, в спектрі випромінювання спостерігається сукупність спектральних ліній, частоти яких визначаються узагальненою формулою Бальмера (20.4). При цьому утворюються спектральні серії - групи ліній, які обумовлені переходами електрона на заданий нижчій рівень n1 з усіх вищих рівнів n2 = n1 +1, n1 +2,… |
|
|
|
|
2) |
Якщо електрон знаходився в стані з головним квантовим числом n1, то при поглинанні кванта енергії \(h\nu\) він перейде в стан з головним квантовим числом n2 за умови \(h\nu=E_{2}-E_{1}\), де E1, E2 – енергії, що відповідають головним квантовим числам n2 та n2. Строго кажучи, енергія фотона повинна бути дещо більшою, оскільки частина енергії та імпульсу фотона передається атому як цілому і надає йому деяку швидкість. Однак цей ефект незначний і в елементарній фізиці не враховується. |
|
|
|
|
3) |
Атом Гідрогену може переходити в збуджений стан у результаті зіткнення з іншими атомами. В такому випадку зберігається імпульс системи та її повна енергія (вона включає кінетичну енергію атомів, енергію електрона в атомі до і після зіткнення, а при необхідності й енергію фотона). |
Задача 20.1. Згідно з теорією Бора, електрон в атомі Гідрогену може рухатися тільки по таких колових орбітах, для яких добуток імпульсу електрона на довжину орбіти кратний сталій Планка: \(mv\cdot{2}\pi{r}=nh\), n = 1, 2, 3,… Виходячи з цього, визначити кутову швидкість електрона \(\omega\) на другій орбіті (n = 2).
Задача 20.2. У спектрі випромінювання атомарного Гідрогену при заданих умовах збудження спостерігається тільки три спектральні лінії. Визначити довжини хвиль цих ліній \(\lambda_{1}\), \(\lambda_{2}\), \(\lambda_{3}\).
Задача 20.3. Збуджені атоми Гідрогену знаходяться на n-ому енергетичному рівні. Визначити повну кількість ліній N, що спостерігаються у спектрі випромінювання цих атомів.
Задача 20.4. Електрон в нерухомому атомі Гідрогену знаходиться на енергетичному рівні n2 = 2. Визначити швидкість v руху атома після випромінювання фотона.
Задача 20.5. На нерухомий атом Гідрогену налітає інший атом Гідрогену. До зіткнення обидва атоми знаходилися в основному стані (n1 = 1). Визначити мінімальну кінетичну енергію W1, яку повинен мати рухомий атом, щоб при прямому непружному зіткненні один з атомів випустив фотон.
Задача 20.1
Згідно з теорією Бора, електрон в атомі Гідрогену може рухатися тільки по таких колових орбітах, для яких добуток імпульсу електрона на довжину орбіти кратний сталій Планка:
\(mv\cdot{2}\pi{r}=nh\), n = 1, 2, 3,…
Виходячи з цього,
визначити
кутову швидкість електрона \(\omega\) на другій орбіті (n = 2).
|
Дано: \(mv\cdot{2}\pi{r}=nh\)
n = 2
|
|
ω - ?
|
Розв’язання
В теорії Бора рух електрона в атомі Гідрогену навколо ядра розглядається як рух точкового заряду під дією кулонівської сили, яка створює доцентрове прискорення. Тому згідно з рівнянням (2.5) та формулами (10.3) і (2.17) можна записати
|
\(\frac{ke^{2}}{r^{2}}=m\omega{r}\) \(\Rightarrow\) \(ke^{2}=m\omega^{2}r^{3}\), |
(1) |
де \(\omega\) – шукана кутова швидкість електрона, \(m=9,1\cdot{10}^{-31}\) кг – його маса,
\(k=\frac{1}{4\pi\varepsilon_{0}}=9\cdot{10}^{9}\) м/Ф.
Крім того враховано, що заряди електрона та ядра атома Гідрогену по модулю рівні \(e=1,6\cdot{10}^{-19}\) Кл. Зробимо в заданій у тексті задачі умові стаціонарності заміни \(v=\omega\cdot{r}\), \(h=h/2\pi=\hbar\), і об’єднаємо її з рівнянням (1):
\(\left\{ \begin{matrix} n\hbar=m\omega{r}^{2} \\ m\omega^{2}r^{3}=ke^{2} \\ \end{matrix} \right.\).
Розв’язавши отриману систему відносно , дістанемо
\(\omega=\frac{k^{2}e^{4}m}{\hbar^{3}n^{3}}=\frac{(9\cdot{10}^{9})^{2}\dot(1,6\cdot{10}^{-19})^{4}\cdot{9,1}\cdot{10}^{-31}}{(1,05\cdot{10}^{-34})^{3}2^{3}}=5,2\cdot{10}^{15}\) c-1.
Задача 20.2
У спектрі випромінювання атомарного Гідрогену при заданих умовах збудження спостерігається тільки три спектральні лінії.
Визначити
довжини хвиль цих ліній \(\lambda_{1}\), \(\lambda_{2}\), \(\lambda_{3}\).
|
Дано: N = 3 |
|
λ1, λ2, λ3 - ?
|
Розв’язання
Згідно з квантовим механізмом випромінювання і умовою (20.1) атом Гідрогену випромінює фотон при переході електрона з будь-якого збудженого енергетичного рівня на будь-який з більш низьких рівнів.
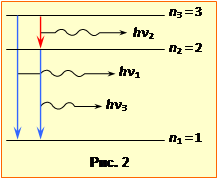 Якщо нижчий рівень сам є збудженим, то через короткий час (час життя збудженого стану) електрон знову переходить на один з більш низьких рівнів. Так продовжується, доки електрон не опиниться в основному стані. З наведених міркувань і схеми енергетичних рівнів (рис.2) неважко збагнути, що найвищий рівень, на якому знаходяться електрони в умовах задачі, відповідає головному квантовому числу n3 = 3. Тільки в цьому випадку можливі лише три переходи, показані стрілками на рис.2, і відповідно - три спектральні лінії з енергіями фотонів \(h\nu_{1}\), \(h\nu_{2}\), \(h\nu_{3}\). Частоти \(\nu_{1}\), \(\nu_{2}\), \(\nu_{3}\) визначаються формулою Бальмера (20.4). Врахувавши значення R = 3,29·1015 Гц, отримаємо
Якщо нижчий рівень сам є збудженим, то через короткий час (час життя збудженого стану) електрон знову переходить на один з більш низьких рівнів. Так продовжується, доки електрон не опиниться в основному стані. З наведених міркувань і схеми енергетичних рівнів (рис.2) неважко збагнути, що найвищий рівень, на якому знаходяться електрони в умовах задачі, відповідає головному квантовому числу n3 = 3. Тільки в цьому випадку можливі лише три переходи, показані стрілками на рис.2, і відповідно - три спектральні лінії з енергіями фотонів \(h\nu_{1}\), \(h\nu_{2}\), \(h\nu_{3}\). Частоти \(\nu_{1}\), \(\nu_{2}\), \(\nu_{3}\) визначаються формулою Бальмера (20.4). Врахувавши значення R = 3,29·1015 Гц, отримаємо
\(\nu_{1}=3,29\cdot{10}^{15}\left(1-\frac{1}{9}\right)=2,93\cdot{10}^{15}\) Гц,
\(\nu_{2}=3,29\cdot{10}^{15}\left(\frac{1}{4}-\frac{1}{9}\right)=4,58\cdot{10}^{14}\) Гц ,
\(\nu_{3}=3,29\cdot{10}^{15}\left(1-\frac{1}{4}\right)=2,47\cdot{10}^{15}\) Гц.
Довжини хвиль визначаються формулою (15.4a), отже
\(\lambda_{1}=\frac{c}{\nu_{1}}=\frac{3\cdot{10}^{8}}{2,93\cdot{10}^{15}}=102,7\) нм;
\(\lambda_{1}=\frac{c}{\nu_{1}}=\frac{3\cdot{10}^{8}}{4,58\cdot{10}^{14}}=656\) нм;
\(\lambda_{1}=\frac{c}{\nu_{1}}=\frac{3\cdot{10}^{8}}{2,47\cdot{10}^{15}}=121\) нм;
Задача 20.3
Збуджені атоми Гідрогену знаходяться на n-ому енергетичному рівні.
Визначити
повну кількість ліній N, що спостерігаються у спектрі випромінювання цих атомів.
|
Дано: n
|
|
N - ?
|
Розв’язання
 На рис. 3 схематично показані всі енергетичні рівні, на яких можуть перебувати електрони за умовою задачі.
На рис. 3 схематично показані всі енергетичні рівні, на яких можуть перебувати електрони за умовою задачі.
Відповідь на поставлене запитання можна отримати прямим підрахунком, взявши до уваги, що шукане число N дорівнює сумі кількостей всіх можливих переходів електронів на кожен з рівнів від першого до (n –1)-го. Очевидно, що таких можливих переходів є:
на перший рівень – n - 1,
на другий рівень – n – 2,
на третій рівень – n – 3,
………………………………………….
на (n - 1)-й рівень – 1.
Отримана числова послідовність є арифметичною прогресією з (n - 1) членів, причому a1 = n - 1, an-1 = 1. Сума арифметичної прогресії дорівнює добутку півсуми першого та останнього членів на їх кількість:
\(N=\frac{(n-1)+1}{2}(n-1)\) \(\Rightarrow\) \(N=\frac{n(n-1)}{2}\).
Примітка. Той, хто знає основи комбінаторики, може отримати відповідь коротше. У кожному переході беруть участь 2 з n рівнів. Тому кількість переходів дорівнює кількості комбінацій з n по 2:
\(N=C_{n}^{2}=\frac{n!}{2!{(n-2)!}}=\frac{(n-1)n}{2}\).
Задача 20.4
Електрон в нерухомому атомі Гідрогену знаходиться на енергетичному рівні n2 = 2.
Визначити
швидкість v руху атома після випромінювання фотона.
|
Дано: \(n_{2}=2\)
|
|
v - ?
|
Розв’язання
Фотон випромінюється при переході електрона зі збудженого рівня n2 = 2 на основний рівень n1 = 1. Енергія фотона W визначається співвідношенням (20.1) і формулою (20.3a):
|
\(W=E_{0}\left(\frac{1}{n_{1}^{2}}-\frac{1}{n_{2}^{2}}\right)=\frac{3E_{0}}{4}\), |
(1) |
де E0 = 13,6 еВ.
Система атом – фотон є ізольованою, тому в ній зберігається імпульс. Оскільки до випромінювання імпульс системи дорівнював нулю, то
\(0=\vec{p}_{ф}+\vec{p}_{а}\) \(\Rightarrow\) \(\vec{p}_{а}=-\vec{p}_{ф}\),
де \(\vec{p}_{а}\), \(\vec{p}_{ф}\) – імпульси атома та випроміненого фотона. Таким чином, атом отримує імпульс "віддачі", рівний за величиною та протилежний за напрямком імпульсу фотона, що випромінюється. Імпульс фотона pф визначається через його енергію W співвідношенням (19.4):
\(p_{ф}=\frac{W}{c}\),
де c – швидкість світла.
В такому разі для модулів маємо:
\(\frac{W}{c}=mv_{а}\) \(\Rightarrow\) \(v=\frac{W}{m_{а}c}\),
де \(m_{а}=1,67\cdot{10}^{-27}\) кг – маса атома Гідрогену. Підставивши в цей вираз значення W з виразу (1), отримаємо
\(v=\frac{3E_{0}}{4m_{а}c}\).
Виразивши величину E0 = 13,6 еВ у джоулях і виконавши обчислення, дістанемо відповідь:
\(v=\frac{3\cdot{13,6}\cdot{1,6}\cdot{10}^{-19}}{4\cdot{1,67}\cdot{10}^{-27}\cdot{3}\cdot{10}^{8}}\approx\) 3,26 м/с.
Примітка. Внаслідок віддачі атом отримує не тільки імпульс, а й деяку кінетичну енергію Wа. Тому, строго говорячи, енергія фотона менша від значення (1) на величину Wа. Але підрахунок показує, що це абсолютно нехтовний ефект:
\(W_{а}=\frac{m_{а}v^{2}}{2}=8,87\cdot{10}^{27}\) Дж = \(5,5\cdot{10}^{-8}\) еВ.
В той же час енергія фотона
\(W=\frac{3\cdot{13,6}}{4}=10,2\) еВ.
Отже Wа << W.
Задача 20.5
На нерухомий атом Гідрогену налітає інший атом Гідрогену. До зіткнення обидва атоми знаходилися в основному стані (n1 = 1).
Визначити
мінімальну кінетичну енергію W1, яку повинен мати рухомий атом, щоб при прямому непружному зіткненні один з атомів випустив фотон.
|
Дано: n1 = 1
|
|
W1 - ?
|
Розв’язання
Зіткнення атомів відбувається з виконанням законів збереження енергії та імпульсу. При непружному зіткненні частина кінетичної енергії налітаючого атома перетворюється на внутрішню енергію, що означає перехід одного або двох атомів у збуджений стан. Мінімальна необхідна енергія очевидно відповідає переходу одного атома з основного стану (n1 = 1) у перший збуджений (n2 = 2). При зворотному переході цей атом випускає фотон.
За законом збереження енергії
|
\(W_{1}=W_{2}+\Delta{W}\), |
(1) |
де W1 – кінетична енергія атома, що налітає, W2 – кінетична енергія атомів після непружного зіткнення, \(\Delta{W}\) – зміна внутрішньої енергії, тобто енергія збудження.
Згідно виразами (20.1) і (20.3a)
|
\(\Delta{W}=E_{0}\left(\frac{1}{n_{1}^{2}}-\frac{1}{n_{2}^{2}}\right)\). |
(2) |
За законом збереження імпульсу
|
\(p_{1}=p_{2}\), |
(3) |
де p1 – імпульс атома, що налітає, p2 – імпульс атомів після непружного удару.
Імпульс і кінетична енергія зв'язані співвідношенням (4.3б)
\(W=\frac{p^{2}}{2m}\) \(\Rightarrow\) \(p=\sqrt{2mW}\).
Тому вираз (3) можна записати у вигляді
|
\(\sqrt{2mW_{1}}=\sqrt{2\cdot{2}nW_{2}}\) \(\Rightarrow\) \(W_{1}=2W_{2}\), |
(4) |
де враховано, що після непружного удару атоми рухаються разом, як одна частинка з масою 2m (m – маса одного атома). З огляду на вирази (2) і (4), формула (1) набуває вигляду
\(W_{1}=\frac{W_{1}}{2}+E_{0}\left(\frac{1}{n_{1}^{2}}-\frac{1}{n_{2}^{2}}\right)\) \(\Rightarrow\) \(W_{1}=E_{0}\left(\frac{1}{n_{1}^{2}}-\frac{1}{n_{2}^{2}}\right)\).
Підставивши сюди значення E0 = 13,6 еВ, n1 = 1, n2 = 2, дістанемо:
\(W_{1}=2\cdot13,6\cdot\left(1-\frac{1}{4}\right)\) = 20,4 еВ.