ФІЗИКА. Вчимося розв'язувати задачі. "СУЧАСНА ФІЗИКА". Компенсаційний курс
Приклади розв'язування задач
Задача 18.1. Визначити власну довжину стержня l0, якщо в лабораторній системі відліку його швидкість v = c/2, довжина l = 1,00 м і кут між ним і напрямком руху \(\theta=45^{\circ}\).
Задача 18.2. Власний час життя нестабільної елементарної частинки \(\Delta{t}_{0}=10\) нс. У лабораторній системі відліку, відносно якої частинка рухається, час її життя \(\Delta{t}=20\) нс. Визначити відстань l, яку пролітає частинка в лабораторній системі відліку до розпаду.
Задача 18.3. Стержень пролітає з постійною швидкістю повз мітку, зроблену в нерухомій K- системі відліку. Час прольоту за годинником K-системи \(\Delta{t}=20\) нс. У системі відліку K’, зв'язаній зі стержнем, мітка рухається повз нього протягом \(\Delta{t}^{\prime}=25\) нс. Визначити власну довжину стержня l0.
Задача 18.4. Дві частинки рухаються назустріч одна одній зі швидкостями v1 = 0,50c і v2 = 0,75c (c – швидкість світла). Визначити: А) відносну швидкість частинок vвідн; Б) швидкість u, з якою зменшується відстань між частинками в лабораторній системі відліку.
Задача 18.5. Швидкість частинки відрізняється від швидкості світла на k = 0,01 %. Визначити відношення релятивістської маси частинки до її маси спокою m/m0.
Задача 18.6. Протон має імпульс p = 10,0 ГеВ/с, де – швидкість світла. Визначити відносну відміну k (у %) швидкості протона від швидкості світла c.
Задача 18.7. Визначити імпульс протона p, кінетична енергія котрого T = 500 МеВ.
Задача 18.8. Визначити роботу A, яку необхідно виконати, щоб змінити швидкість протона від v1 = 0,6c до v2 = 0,8c.
Задача 18.9. Енергія сонячного випромінювання, яке нормально падає щосекунди на одиничну площадку на поверхні Землі, дорівнює I = 1,4 кДж/(м2·с) (ця величина називається сонячною сталою і не враховує поглинання та розсіювання сонячного випромінювання атмосферою Землі). Прийнявши середній радіус земної орбіти R = 149,5·106 км і масу Сонця M = 2·1030 кг, визначити: А) масу \(\mu\), що втрачає Сонце за одиницю часу; Б) час t, за який маса Сонця зменшилася б на k = 1 % при незмінній інтенсивності випромінювання.
Задача 18.1
Визначити
власну довжину стержня l0, якщо в лабораторній системі відліку його швидкість v = c/2, довжина l = 1,00 м і кут між ним і напрямком руху \(\theta=45^{\circ}\).
|
Дано: v = c/2
l = 1,00 м
\(\theta=45^{\circ}\)
|
|
l0 - ?
|
Розв’язання
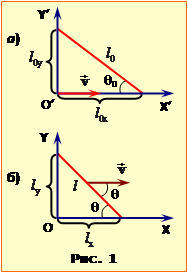 Нехай стержень у власній системі відліку X’O’Y’ (тобто такій, де він перебуває у спокої), розташований так, як показано на рис.1а. Його довжина в цій системі визначається довжинами відрізків l0x і l0y:
Нехай стержень у власній системі відліку X’O’Y’ (тобто такій, де він перебуває у спокої), розташований так, як показано на рис.1а. Його довжина в цій системі визначається довжинами відрізків l0x і l0y:
|
\(l_{0}=\sqrt{l_{0x}^{2}+l{oy}^{2}}\). |
(1) |
Для спостерігача лабораторної системи відліку XOY довжини відрізків, що відсікаються кінцями стержня на осях OX та OY, згідно з формулою (18.1), рівні:
\(l_{x}=l_{0x}\sqrt{1-\beta^{2}}\), \(l_{y}=l_{0y}\),
де \(\beta=v/c\). З рис.1б зрозуміло, що
\(l_{x}=l\cos\theta\), \(l_{y}=l\sin\theta\).
Тому
\(l_{0x}=\frac{l\cos\theta}{\sqrt{1-\beta^{2}}}\), \(l_{0y}=l\sin\theta\).
Підставивши ці вирази у формулу (1), одержимо:
\(l_{0}=l\sqrt{\frac{1-\beta^{2}\sin^{2}\theta}{1-\beta^{2}}}=1,00\cdot\sqrt{\frac{1-0,25\cdot{0,5}}{1-0,25}}=1,08\) м.
Задача 18.2
Власний час життя нестабільної елементарної частинки \(\Delta{t}_{0}=10\) нс. У лабораторній системі відліку, відносно якої частинка рухається, час її життя \(\Delta{t}=20\) нс.
Визначити
відстань l, яку пролітає частинка в лабораторній системі відліку до розпаду.
|
Дано: Δt0 = 10 нс
Δt = 20 нс
|
|
l - ?
|
Розв’язання
Проміжок часу між двома подіями в різних системах відліку зв'язаний співвідношенням (18.2):
\(\Delta{t}=\frac{\Delta{t}_{0}}{\sqrt{1-\beta^{2}}}\),
де \(\beta=v/c\). З цього співвідношення визначаємо швидкість руху частинки в заданій системі відліку
\(v=c\sqrt{1-(\Delta{t}_{0}/\Delta{t})^{2}}\).
Пройдений частинкою шлях
\(l=v\cdot\Delta{t}=c\cdot\Delta{t}\sqrt{1-(\Delta{t}_{0}/\Delta{t})^{2}}=3\cdot{10}^{8}\cdot{20}\cdot{10}^{-9}\cdot\sqrt{1-(10/20)^{2}}\approx{5,2}\) м.
Примітка
Під коренем стоїть відношення проміжків часу, тому при обчисленнях можна користуватися будь-якими, але однаковими, одиницями часу.
Задача 18.3
Стержень пролітає з постійною швидкістю повз мітку, зроблену в нерухомій K- системі відліку. Час прольоту за годинником K-системи \(\Delta{t}=20\) нс. У системі відліку K’, зв'язаній зі стержнем, мітка рухається повз нього протягом \(\Delta{t}^{\prime}=25\) нс.
Визначити
власну довжину стержня l0.
|
Дано: Δt = 20 нс
Δt′ = 25 нс
|
|
l0 - ?
|
Розв’язання
Для спостерігача K- системи відліку час прольоту стержня
|
\(\Delta{t}={l}/{v}\), |
(1) |
де v – швидкість стержня, l – його довжина в K – системі, яка зв'язана з власною довжиною l0 співвідношенням (18.1):
|
\(l=l_{0}\sqrt{1-\beta^{2}}\), |
(2) |
де \(\beta=v/c\).
У K′- системі стержень нерухомий і має довжину l0, тому час прольоту мітки повз нього
|
\(\Delta{t}^{\prime}=\frac{l_{0}}{v}\). |
(3) |
Підставивши у формулу (1) вираз (2) і врахувавши (3), знаходимо
\(\Delta{t}=\Delta{t}^{\prime}\sqrt{1-\beta^{2}}\) \(\Rightarrow\) \(v=c\sqrt{1-(\Delta{t}/\Delta{t}^{\prime})^{2}}\).
Підставивши це значення у формулу (3), одержимо
\(l_{0}=c\cdot\Delta{t}^{\prime}\cdot\sqrt{1-(\Delta{t}/\Delta{t}^{\prime})^{2}}=3\cdot{10}^{8}\cdot{2,5}\cdot{10}^{-8}\sqrt{1-(20/25)^{2}}=4,5\) м.
Задача 18.4
Дві частинки рухаються назустріч одна одній зі швидкостями v1 = 0,50c і v2 = 0,75c (c – швидкість світла).
Визначити:
А) відносну швидкість частинок vвідн;
Б) швидкість u, з якою зменшується відстань між частинками в лабораторній системі відліку.
|
Дано: v1 = 0,50c
v2 = 0,75c
|
|
vвідн - ?
u - ?
|
Розв’язання
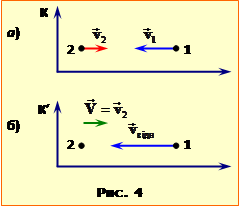 A) Для визначення відносної швидкості частинок перейдемо в систему відліку K′, яка має швидкість \(\vec{V}=\vec{v}_{2}\) відносно системи відліку K (рис.4). Тоді швидкість частинки 2 в K′ – системі \(\vec{v}_{2}^{\prime}=0\). Швидкість частинки 1 \(\vec{v}_{1}^{\prime}\) – то є швидкість її руху відносно частинки 2, тобто – шукана відносна швидкість: \(\vec{v}_{відн}=\vec{v}_{1}^{\prime}\). Отже, згідно з формулою (18.3), відносна швидкість частинок
A) Для визначення відносної швидкості частинок перейдемо в систему відліку K′, яка має швидкість \(\vec{V}=\vec{v}_{2}\) відносно системи відліку K (рис.4). Тоді швидкість частинки 2 в K′ – системі \(\vec{v}_{2}^{\prime}=0\). Швидкість частинки 1 \(\vec{v}_{1}^{\prime}\) – то є швидкість її руху відносно частинки 2, тобто – шукана відносна швидкість: \(\vec{v}_{відн}=\vec{v}_{1}^{\prime}\). Отже, згідно з формулою (18.3), відносна швидкість частинок
\(v_{відн}=\frac{v_{1}-v_{2}}{1+v_{1}\cdot{v}_{2}/c^{2}}=-\frac{0,5c+0,75c}{1+0,5c\cdot{0,75}c/c^{2}}=-\frac{1,25c}{1,376}=-0,91c=-2,73\cdot{10}^{8}\) м/с.
Знак "–" вказує напрям руху частинки 1 (протилежно напрямку осі OX).
Зауважимо, що навіть якби швидкості частинок були рівні c (частинки – фотони), їхня відносна швидкість була б
\(v_{відн}=\frac{c+c}{1+c\cdot{c}/c^{2}}=c\).
Це ілюструє граничність швидкості c.
Б) У лабораторній системі відліку частинки проходять за час t відстані l1 = v1t і l2 = v2t наближаючись одна до одної на відстань l = v1t + v2t = (v1 + v2)t Отже швидкість u з якою зменшується відстань між частинками в лабораторній системі відліку,
\(u=\frac{l}{t}=v_{1}+v_{2}=0,5c+0,75c=1,25c\).
Те, що отримана величина u > c ніяк не суперечить існуванню в природі граничної швидкості c. Знайдена величина є швидкістю зміни відстані між частинками для стороннього спостерігача. Але вона не є швидкістю руху жодної з частинок.
Задача 18.5
Швидкість частинки відрізняється від швидкості світла на k = 0,01 %.
Визначити
відношення релятивістської маси частинки до її маси спокою m/m0.
|
Дано: k = 0,01 %
|
|
m/m0 - ?
|
Розв’язання
Згідно з формулою (18.5)
|
\(\frac{m}{m_{0}}=\frac{1}{\sqrt{1-\beta^{2}}}\), |
(1) |
де \(\beta=v/c\), v – швидкість частинки, c – швидкість світла.
За умовою задачі
\(k=\frac{c-v}{c}\) \(\Rightarrow\) \(v=(1-l)\cdot{c}\) \(\Rightarrow\) \(\beta=1-k\)
Підставивши це значення у вираз (1), знаходимо
\(\frac{m}{m_{0}}\frac{1}{\sqrt{2k+k^{2}}}\approx\frac{1}{\sqrt{2k}}=70,7\)..
де ми знехтували k2 у порівнянні з 2k у зв'язку з малістю цієї величини.
Задача 18.6
Протон має імпульс p = 10,0 ГеВ/с, де – швидкість світла.
Визначити
відносну відміну k (у %) швидкості протона від швидкості світла c.
|
Дано: p = 10,0 ГеВ/с
|
|
k (%) - ?
|
Розв’язання
Відносна відміна швидкості частинки від швидкості світла визначається виразом
|
\(k=\frac{c-v}{c}=1-\frac{v}{c}=1-\beta\), |
(1) |
де \(\beta=v/c\).
Таким чином, розв'язання задачі зводиться до визначення \(\beta\). Для цього скористаємося виразом релятивістського імпульсу (18.4):
\(p=\frac{m_{0}v}{\sqrt{1-\beta^{2}}}\),
де m0 – маса спокою частинки.
Домножимо обидві частини на \(c^{2}\) і піднесемо цей вираз до квадрата:
\((pc^{2})^{2}=\frac{(m_{0}c^{2})^{2}v^{2}}{1-\beta^{2}}\) \(\Rightarrow\) \(\frac{p^{2}c^{2}}{E_{0}^{2}}=\frac{\beta^{2}}{1-\beta^{2}}\),
де \(E_{0}=m_{0}c^{2}=938,3\) МеВ – енергія спокою протона.
З цієї рівності після перетворень знаходимо \(\beta\)
\(\beta=\frac{1}{\sqrt{(E_{0}/pc)^{2}+1}}\),
і з виразу (1) дістаємо відповідь:
\(k=1-\frac{1}{\sqrt{(E)_{0}/pc)^{2}+1}}=1-\frac{1}{\sqrt{(938,3/10\cdot{10}^{3})^{2}+1}}=0,00473\approx0,44\) %.
Примітка. Для елементарних частинок основні одиниці виміру енергії (Дж) і імпульсу (кг·м/с) дуже незручні – занадто великі. Тому використовують позасистемні одиниці енергії: електрон-вольт (1 еВ = \(1,6\cdot{10}^{-19}\) Дж), мегаелектрон-вольт (читається «мев», 1 МеВ = \(10^{6}\) еВ) і гігаелектрон-вольт («гев», 1 ГеВ = \(10^{9}\) еВ). Для імпульсу швидких (релятивістських) частинок теж застосовують специфічну одиницю 1 ГеВ/с, де с – швидкість світла у вакуумі (а не позначення секунди). Це дуже зручно, тому що числові значення імпульсу в таких одиницях дорівнюють величині pc, яка часто зустрічається в задачах релятивістської механіки.
Задача 18.7
Визначити
імпульс протона p, кінетична енергія котрого T = 500 МеВ.
|
Дано: T = 500 МеВ
|
|
p - ?
|
Розв’язання
З формул повної енергії релятивістської частинки (18.6) і (18.6а) маємо:
|
\(mc^{2}=\frac{m_{0}c^{2}}{\sqrt{1-\beta^{2}}}\), |
(1) |
де \(\beta=v/c\).
Після піднесення до квадрата виразу (1), одержимо
\(m^{2}c^{4}=\frac{m_{0}^{2}c^{4}}{1-\beta^{2}}\) \(\Rightarrow\) \(m^{2}c^{4}-m^{2}v^{2}c^{4}=m_{0}^{2}c^{4}\).
Врахувавши, що \(m_{0}c^{2}=E_{0}\) – енергія спокою (формула (18.6б)) і mv = p – релятивістський імпульс (формула (18.4а)), отримуємо:
|
\(E^{2}-p^{2}c^{2}=E_{0}^{2}\) \(\Rightarrow\) \(p=\frac{1}{c}\sqrt{E^{2}-E_{0}^{2}}\). |
(2) |
Повна енергія E дорівнює сумі кінетичної енергії T і енергії спокою E0:
E = E0 + T.
Підставивши цей вираз у формулу (2), знаходимо:
\(p=\frac{1}{c}\sqrt{T(T+2E_{0})}\).
З довідкових таблиць для протона \(E_{0}=938,3\) МеВ. Крім того використаємо зручну одиницю імпульсу ГеВ/с (див. задачу 18.6):
\(p=\frac{1}{c}\sqrt{500(500+2\cdot{938,3})}=1090\ \frac{МеВ}{c}=1,09\ \frac{ГеВ}{c}\)
В одиницях СІ:
p = 5,8·10-19 кг·м/с.
Задача 18.8
Визначити
роботу A, яку необхідно виконати, щоб змінити швидкість протона від v1 = 0,6c до v2 = 0,8c.
|
Дано: v1 = 0,6c
v2 = 0,8c
|
|
A - ?
|
Розв’язання
Виконана над частинкою робота дорівнює зміні її кінетичної енергії (рівняння (4.4). Кінетична енергія релятивістської частинки визначається виразом (18.9), отже
\(A=T_{2}-T_{1}=E_{0}\left(\frac{1}{\sqrt{1-\beta_{2}^{2}}}-1\right)- \left(\frac{1}{\sqrt{1-\beta_{1}^{2}}}-1\right)=E_{0}\left(\frac{1}{\sqrt{1-\beta_{2}^{2}}}-\frac{1}{\sqrt{1-\beta_{2}^{2}}}\right)\).
де \(\beta_{1}=v_{1}/c\), \(\beta_{2}=v_{2}/c\).
Підставивши в цей вираз числові значення v1 = 0,6c, v2 = 0,8c і табличне значення для протона E0 = 938,3 МеВ, одержимо
\(A=938,3\left(\frac{1}{\sqrt{1-0,64}}-\frac{1}{\sqrt{1-0,36}}\right)\approx{391}\) МеВ.
Задача 18.9
Енергія сонячного випромінювання, яке нормально падає щосекунди на одиничну площадку на поверхні Землі, дорівнює I = 1,4 кДж/(м2·с) (ця величина називається сонячною сталою і не враховує поглинання та розсіювання сонячного випромінювання атмосферою Землі). Прийнявши середній радіус земної орбіти R = 149,5·106 км і масу Сонця M = 2·1030 кг,
Визначити:
А) масу \(\mu\), що втрачає Сонце за одиницю часу;
Б) час t, за який маса Сонця зменшилася б на k = 1 % при незмінній інтенсивності випромінювання.
|
Дано: I = 1,4 кДж/(м2·с) = 1,4·103 Дж/(м2·с)
R = 149,5·106 км = 1,495·1011 м
M = 2·1030 кг
k = 1 %
|
|
\(\mu\) - ?
t - ?
|
Розв’язання
А) Зменшення маси Сонця відбувається внаслідок випромінювання енергії. Відповідно до співвідношення (18.7), шукана втрата маси
|
\(\mu=W/c^{2}\), |
(1) |
де W – енергія, що випромінюється Сонцем за 1 c по всіх напрямках.
Зрозуміло, що на площадку \(\Delta{S}\), що розташована на відстані R від Сонця, припадає частка цієї енергії, рівна
\(\Delta{W}=\frac{W}{4\pi{R}^{2}}\Delta{S}\).
Відповідно на одиницю площі за 1 c падає енергія
\(I=\frac{W}{4\pi{R}^{2}}\).
Підставивши цей вираз у формулу (1), одержимо шукану втрату маси:
\(\mu=\frac{W\cdot{4}\pi{R}^{2}}{c^{2}}=\frac{1,4\cdot{10}^{3}\cdot{4}\pi\cdot{(1,49\cdot{10}^{11})^{2}}}{(3\cdot{10}^{8})^{2}}\approx4,3\cdot{10}^{9}\) кг/с.
Б) Втрата маси Сонця за шуканий час за умовою становить
\(\Delta{m}=kM\).
З іншого боку \(\Delta{m}=\mu\cdot{t}\) (\(\mu\) – втрата маси за одиницю часу), отже
\(t=\frac{\Delta{m}}{\mu}=\frac{kM}{\mu}=\frac{0,01\cdot{2}\cdot{10}^{30}}{4,3\cdot{10}^{9}}=4,65\cdot{10}^{18}\) c,
що складає приблизно 150 мільярдів років.