ФІЗИКА. Вчимося розв'язувати задачі. "ОПТИКА". Компенсаційний курс
Розділ 17. Хвильова оптика
Теоретичні відомості. Дифракція світла
|
Якщо на шляху поширення хвиль трапляються різкі неоднорідності, то спостерігається дифракція. На явищі дифракції світла заснована дія оптичного приладу, що зветься дифракційною граткою. Дифракційна гратка має важливі практичні застосування. |
|
Дифракцією називаються явища, зумовлені здатністю хвиль змінювати напрям поширення при зустрічі з різкими неоднорідностями – невеликими непрозорими перешкодами або з отворами у непрозорому екрані. Можливість практичного спостереження дифракції залежить від розмірів перешкод: вони повинні бути співвимірними з довжиною хвилі (оптимально – (10 – 100)\(\lambda\). Дифракційні явища можна аналізувати на основі принципу Гюйгенса-Френеля, згідно з яким
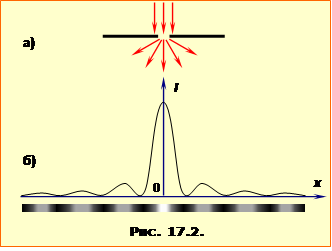
Оскільки вторинні хвилі когерентні, то при накладанні вони інтерферують з утворенням максимумів і мінімумів інтенсивності. З цієї причини при проходженні світла крізь малий отвір (рис.17.2а) на поставленому за ним екрані спостерігається не просто розмите зображення отвору, а сукупність світлих і темних смуг (кілець) – дифракційних максимумів і мінімумів (рис.17.2б).
|
|
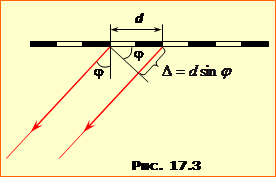
Дифракційні смуги від одного отвору через його малі розміри дуже слабкі. Але інтенсивність дифракційних максимумів різко збільшується у дифракційній гратці. Найпростіша дифракційна гратка являє собою плоску прозору пластинку, на поверхні якої створена система однакових вузьких прозорих смуг (щілин), розділених однаковими непрозорими проміжками (рис.17.3). Відстань d між сусідніми щілинами називається періодом гратки, і є одним з її основних параметрів. Часто замість d використовують сталу дифракційної гратки n = 1/d – кількість щілин на одиницю довжини гратки. Ще одним параметром гратки є загальна кількість щілин N. Для дифракційних граток високого класу d ~ 1 мкм (10-6 м) і N ~ 105.
При опроміненні гратки паралельним пучком променів внаслідок дифракції після неї під будь-яким кутом \(\varphi\) поширюється N когерентних пучків від усіх щілин. Кут, під яким поширюється певний пучок, називають кутом дифракції. В результаті інтерференції цих пучків на розташованому за ґраткою екрані виникає складна дифракційна картина, що складається з великої кількості мінімумів та максимумів різної інтенсивності. Серед них вирізняються дуже інтенсивні головні максимуми. Вони визначаться умовою головних максимумів ґратки:
У цій формулі d – період гратки, \(\varphi\) – кут дифракції (див. рис.17.3), \(\lambda\) – довжина хвилі світла, яким опромінюється гратка, m – ціле число, що називається порядком дифракційного спектра. Умова (17.9) і велика інтенсивність головних максимумів мають просте пояснення. З рис.17.3 можна зрозуміти, що величина \(\Delta=d\sin\varphi \) – то є різниця ходу променів, які йдуть під кутом \(\varphi\) від двох сусідніх щілин. Це означає, що при виконанні умови (17.9) фази коливань електричного поля від усіх N щілин кратні \(2\pi\). Тому результуюча амплітуда \(E=NE_{1}\), а результуюча інтенсивність
де \(I_{1}\) – інтенсивність світла, що створюється однією щілиною, N – загальна кількість щілин гратки. |
|
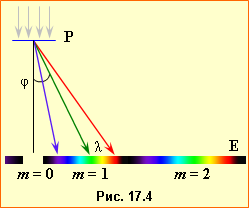
З формули (17.10) випливає, що в головних максимумах спостерігається дуже велика концентрація світлової енергії. Це визначає практичні застосування дифракційної гратки. Згідно з умовою (17.9), кожній довжині хвилі \(\lambda\) відповідає свій власний кут дифракції \(\varphi\), а отже своє власне положення головного максимума при заданому m. Тому, якщо на гратку P з відомим періодом напрямити пучок білого світла (рис.17.4), то на екрані E для всіх \(m\ne{0}\) замість вузьких яскравих смуг утворюються спектри – широкі смуги, що забарвлені у кольори веселки. У центрі екрана m = 0, \(\sin\varphi=0\) і умова (17.9) виконується для будь-якої довжини хвилі. Тому в центрі екрана спостерігається вузька незабарвлена смуга.
Вимірявши кут дифракції \(\varphi\) (або координату відповідної точки на екрані), можна визначити довжину хвилі \(\lambda\) світла, що дає дифракційний максимум у даній точці екрана: \(\lambda=\frac{d\sin\varphi}{m}\). Властивість дифракційної гратки розгортати світло у спектр використовується в оптичних приладах для отримання монохроматичного світла та для визначення спектрального складу невідомого випромінення. |