ФІЗИКА. Вчимося розв'язувати задачі. "ОПТИКА". Компенсаційний курс
Приклади розв’язування задач
Рекомендації до теми "Побудова зображень у дзеркалах і лінзах"
|
Задачі на побудову зображень передбачають виконання певних "правил гри":
При розв'язуванні графічних задач на дзеркала та лінзи корисно керуватись такими порадами. |
|
1) |
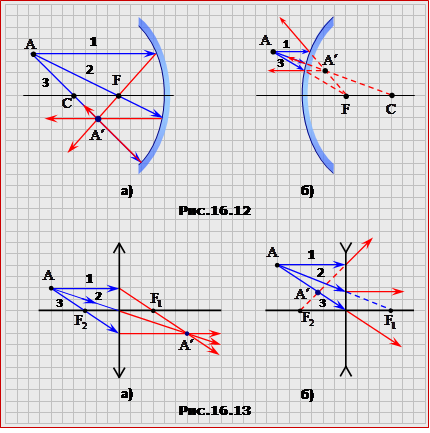
Всі промені, що виходять з однієї точки "предмета", після лінзи (дзеркала) перетинаються (самі чи їх продовження) теж в одній точці - зображенні. Тому для отримання зображення точки А необхідно і достатньо побудувати хід через лінзу (дзеркало) будь-яких двох променів, що виходять з цієї точки. Зображення А' знаходиться на перетині цих променів (або їхніх продовжень). Звичайно для побудови використовують будь-які два з трьох "зручних" променів, хід яких заздалегідь відомий. Ці зручні промені, а також побудова зображення точки, показані на рис.16.12 для дзеркал і на рис.16.13 - для лінз.
Примітка. Промені 2, що падають в оптичний центр тонкої лінзи, проходять без відхилення і зміщення через те, що поверхні лінзи в області центра взаємно паралельні, і відстань між ними гранично мала. |
|
|
|
|
2) |
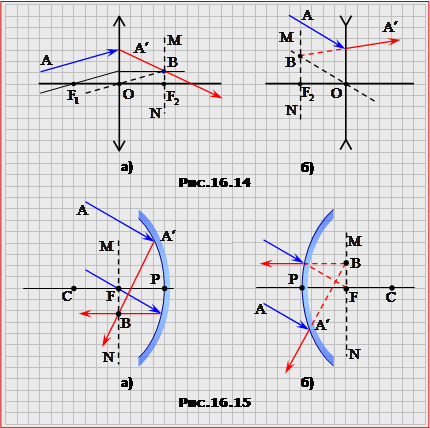
В деяких задачах за умовою можна використати тільки один з названих зручних променів (наприклад, треба побудувати зображення точки, що лежить на головній оптичній осі лінзи (дзеркала), як на рис.16.11д). Відтак другим необхідним для побудови може бути довільний промінь. Хід довільного променя після лінзи (дзеркала) будується з використанням фокальної площини. Побудову ходу довільного променя АА' для лінз показано на рис.16.14 (а) - збірна лінза, б) - розсівна лінза), а для дзеркал - на рис.16.15 (а) - увігнуте дзеркало, б) - опукле дзеркало).
Побудова виконується у такій послідовності: а) проводиться робоча фокальна площина MN (у збірній лінзі вона знаходиться за лінзою, а в розсіювальній - перед лінзою); б) паралельно до заданого променя АА' проводиться допоміжний промінь з відомим подальшим ходом і знаходиться точка В його перетину з фокальною площиною; шуканий заломлений (відбитий) промінь проходить через точки А' и В. (Примітка. Для такої побудови можна використовувати бути якийсь з трьох розглянутих вище "зручних" променів (рис.16.13). Звичайно вибирають той, що проходить найближче до заданого: при цьому легше витримати паралельність допоміжного та заданого променів). |
|
|
|
|
3) |
В деяких задачах на побудову необхідно визначати положення і характеристики лінзи (дзеркала) за заданим положенням точки та її зображення. При розв'язуванні таких задач необхідно пам'ятати, що:
Точка A та її зображення A' у випадку дійсного зображення розташовані по різні боки головної оптичної осі (рис.16.12а, 16.13а), а у випадку уявного зображення - по один бік (рис.16.12б, 16.13б). |
|
|
|
|
4) |
Для більшої виразності креслення усі дійсні промені має сенс проводити суцільними лініями, а всі уявні - штриховими; допоміжні промені, на відміну від основних, доцільно проводити тоншими лініями. |