ФІЗИКА. Вчимося розв'язувати задачі. "КОЛИВАННЯ ТА ХВИЛІ". Компенсаційний курс

При розв'язуванні задач на енергію гармонічних коливань часто буває необхідно скласти рівняння енергетичного балансу (13.21a) з використанням виразів (13.19), (13.20), (13.21).

У зв'язку з цим нагадаємо, що формули (13.20) і (13.19) можна застосоувати не лише до коливань вантажу на пружині, але й до будь-яких інших гармонічних коливань. При цьому k - коефіцієнт пропорційності між рівнодійною силою і зміщенням тіла з положення рівноваги.

Нагадаємо також, що вигляд тригонометричної функції в рівняннях (13.19) та (13.20) не відомий заздалегідь, а залежить від вибору вихідної функції, що описує коливання.

Задача 13.8. Математичний маятник з довжиною нитки l здійснює малі коливання. Показати, що потенціальна енергія малих коливань маятника визначається формулою (13.19): \(W_{п}=\frac{kx^{2}}{2}\), в якій коефіцієнт k задається виразом (13.16): \(k=\frac{mg}{l}\).

Задача 13.9. Тіло, прикріплене до пружини, здійснює гармонічні коливання, амплітуда коливань A = 2 см. Повна енергія коливань W = 0,3 мДж. Визначити зміщення x з положення рівноваги, при якому на тіло діє повертаюча сила |F| = 22,5 мН.

Задача 13.10. Тіло, прикріплене до пружини жорсткістю k = 1200 Н/м, Здійснює в горизонтальній площині коливання за законом синуса з амплітудою A = 10 см. Нехтуючи тертям і опором повітря, визначити повну W, кінетичну W_к  і потенціальну W_п енергії коливань при фазі \(\varphi=50^{\circ}\).

Задача 13.11. Тіло, прикріплене до пружини, здійснює гармонічні коливання в горизонтальній площині. В момент, коли потенціальна енергія системи складає n = 80 % її повної енергії, зміщення тіла з положення рівноваги  x = 2 см, а його швидкість v = 3,1 см/с. Визначити період коливань T.

Задача 13.8

Математичний маятник з довжиною нитки l здійснює малі коливання.

Показати,
що потенціальна енергія малих коливань маятника визначається формулою (13.19): \(W_{п}=\frac{kx^{2}}{2}\), в якій коефіцієнт k задається виразом (13.16): \(k=\frac{mg}{l}\).

Розв’язання

Потенціальна енергія маятника обумовлена дією на нього сили тяжіння і виражається формулою

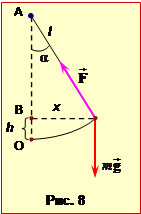
де m – маса маятника, h – висота підйому над положенням рівноваги (див. рис.8). З рис.8 видно, що

Оскільки маятник здійснює малі коливання (\(x\ll{l}\)), то \(\alpha\ll{1}\) рад. Тому \(\sin\frac{\alpha}{2}=\frac{\alpha}{2}\), і вираз (2) набуває вигляду:

\(h=2l\left(\frac{\alpha}{2}\right)^{2}=\frac{l\alpha^{2}}{2}\).

Підставивши його у формулу (1) і зробивши заміну \(\alpha=x/l\), отримаємо

\(W_{п}=\frac{mgx^{2}}{2l}=\frac{kx^{2}}{2}\),

де \(k=\frac{mg}{l}\), що і треба було довести.

Ця задача ілюструє універсальність формули (13.19): вона може бути застосовна до будь-яких гармонічних коливань, а не тільки до коливань під дією сили пружності.

 Задача 13.9

Тіло, прикріплене до пружини, здійснює гармонічні коливання, амплітуда коливань A = 2 см. Повна енергія коливань W = 0,3 мДж.

Визначити
зміщення x з положення рівноваги, при якому на тіло діє повертаюча сила |F| = 22,5 мН.

Розв’язання

Повна енергія тіла, що здійснює гармонічні коливання, визначається формулою (13.21):

Повертаюча сила в залежності від зміщеня виражається формулою (13.10), причому її модуль

Виключивши з виразів (1) і (2) величину k, знаходимо:

\(x=\frac{|F|A^{2}}{2W}=\frac{2,25\cdot{10^{-2}}\cdot{4}\cdot{10^{-4}}}{2\cdot{3}\cdot{10^{-4}}}=1,5\cdot{10^{-2}}\) м = 1,5 см.

Задача 13.10

Тіло, прикріплене до пружини жорсткістю k = 1200 Н/м, Здійснює в горизонтальній площині коливання за законом синуса з амплітудою A = 10 см. Нехтуючи тертям і опором повітря,

визначити
повну W, кінетичну W_к  і потенціальну W_п енергії коливань при фазі \(\varphi=50^{\circ}\).

Розв’язання

Повна енергія коливань тіла на пружині визначається виразом (13.21):

\(W=\frac{kA^{2}}{2}=\frac{1200\cdot{10^{-2}}}{2}=6\) Дж.

Згідно з умовою, коливання відбуваються за законом

\(x=A\sin(\omega{t}+\varphi_{0})=A\sin\varphi\),

де \(\varphi=\omega+\varphi_{0}\) – фаза коливань. Потенціальна енергія коливань відповідно до формули (13.19)

\(W_{п}=\frac{kx^{2}}{2}=\frac{kA^{2}\sin^{2}\varphi}{2}\)=\(\frac{1200\cdot{10^{-2}}\sin^{2}50^{\circ}}{2}\) = 3,52 Дж.

Оскільки повна енергія рівна сумі кінетичної і потенціальної W = W_к + W_п, то кінетична енергія коливань

W_к = W – W_п = 6 – 3,52 = 2,48 Дж.

Звичайно, кінетичну енергію можна було б шукати як \(W_{к}=\frac{mv^{2}}{2}\), але для цього треба було б визначати швидкість як похідну від координати x по часу, і врахувати, що амплітуда швидкості \(v_{m}=A\omega\), і далі скористатися тим, що \(k=m\omega^{2}\). Все це вимагає додаткових перетворень, а використання закону збереження енергії дозволило одержати значення кінетичної енергії за одну дію.

Задача 13.11

Тіло, прикріплене до пружини, здійснює гармонічні коливання в горизонтальній площині. В момент, коли потенціальна енергія системи складає n = 80 % її повної енергії, зміщення тіла з положення рівноваги  x = 2 см, а його швидкість v = 3,1 см/с.

Визначити
період коливань T.

Розв’язання

Період коливань тіла на пружині визначається формулою:

Відношення m/k знайдемо з умови збереження повної енергії коливань:

де \(W_{к}=mv^{2}/2\) – кінетична енергія, \(W_{п}=kx^{2}/2\) – потенціальна енергія. З формули (2) одержуємо:

\(\frac{m}{k}=\frac{x^{2}}{v^{2}}\left(\frac{W}{W_{п}}-1\right)\).

Підставивши цей вираз у формулу (1), маємо

\(T=2\pi\frac{x}{v}\sqrt{\frac{W}{W_{п}}-1}=2\pi\cdot\frac{2}{3,1}\sqrt{\frac{1}{0,8}-1}\approx\) 2 c.

Підкреслимо, що методи розв’язування задач, які ґрунтуються на законі збереження енергії, часто дозволяють визначити період (частоту) коливань простіше, ніж інші методи.