ФІЗИКА. Вчимося розв'язувати задачі. "КОЛИВАННЯ ТА ХВИЛІ". Компенсаційний курс
Приклади розв’язування задач
Рівняння і характеристики гармонічних коливань
У задачах, де потрібно складати рівняння гармонічних коливань за заданими характеристиками і початковими умовами, іноді виникають проблеми з визначенням початкової фази. Необхідно пам'ятати, що для визначення початкової фази потрібно використовувати обидві початкові умови (x(0), v(0)), оскільки при використанні тільки однієї з них початкова фаза визначається неоднозначно.
Для визначення характеристик гармонічних коливань за заданим рівнянням необхідно виконати наступне.
|
1) |
Записати загальний вигляд рівняння коливань через ту функцію, що використана в умові задачі. |
|
|
|
|
2) |
Порівнюючи задане числове рівняння із загальним, визначити значення необхідних характеристик (амплітуда, період і ін.). При цьому треба взяти до уваги, що коли в заданому рівнянні не зазначені одиниці фізичних величин, то вони задані в основних одиницях СІ. |
|
|
|
|
3) |
Якщо потрібно визначити якісь характеристики, що не входять у задане рівняння (наприклад, швидкість за заданим рівнянням координати), то спочатку треба із заданого рівняння одержати рівняння коливань необхідної величини, а потім діяти аналогічно п.2). |
Задача 13.1. Точка здійснює гармонічні коливання з періодом T = 1,57 c і амплітудою A = 12 см. Визначити рівняння руху точки x(t), якщо в початковий момент часу її координата x0 = 6 см і вона віддаляється від положення рівноваги.
Задача 13.2. Точка здійснює гармонічні коливання. На відстані x1 = 3 см від положення рівноваги її швидкість v1 = 10 см/с, а на відстані x2 = 5 см – швидкість v2 = 6 см/с. Визначити циклічну частоту \(\omega\) й амплітуду A коливань.
Задача 13.3. Тіло здійснює гармонічні коливання між точками C і D. Його максимальна швидкість \(v_{m}\) = 10 м/с. Визначити середню швидкість \(\langle{v}\rangle\) на шляху від C до D.
Задача 13.1
Точка здійснює гармонічні коливання з періодом T = 1,57 c і амплітудою A = 12 см.
Визначити
рівняння руху точки x(t), якщо в початковий момент часу її координата x0 = 6 см і вона віддаляється від положення рівноваги.
|
Дано: T = 1,57 c
A = 12 см
\(x_{0}\) = 6 см
|
|
x(t) - ?
|
Розв’язання
Оскільки в початковий момент часу ні координата, ні швидкість точки не дорівнюють нулю, то немає значення, яку функцію вибрати для опису коливань. Будемо вважати, що рівняння x(t) має вигляд
|
|
\(x(t)=A\cos\left(\frac{2\pi}{T}t+\varphi_{0}\right)\). |
(1) |
Значення A і T задані, отже, задача зводиться до визначення початкової фази \(\varphi_{0}\). Підставивши в рівняння (1) значення t = 0, x0 і A, одержимо
\(6=12\cos\varphi_{0}\) \(\Rightarrow\) \(\cos\varphi_{0}=\frac{1}{2}\) \(\Rightarrow\) \(\varphi_{0}=\pm\frac{\pi}{3}\).
Для вибору знаку \(\varphi_{0}\) врахуємо, що за умовою у початковий момент часу напрям швидкості точки співпадає з напрямом осі OX, тобто \(v_{0x}>0\). Проекція швидкості \(v_{0x}=x^{\prime}(t)\), тому з рівняння (1):
\(v_{x}=x^{\prime}(t)=-A\frac{2\pi}{T}\cos\left(\frac{2\pi}{T}\cdot{t}+\varphi_{0}\right)\).
При t = 0
\(v_{0x}=-A\frac{2\pi}{T}\sin\varphi_{0}\).
Оскільки \(v_{0x}>0\), то
\(\sin\varphi_{0}<0\) \(\Rightarrow\) \(\varphi_{0}<0\).
Отже, початкова фаза \(\varphi_{0}=-\pi/3\).
Підставивши в рівняння (1) всі числові значення, отримаємо відповідь:
\(x(t)=12\cos\left(4t-\pi/3\right)\), см.
Зауваження. Зверніть увагу на те, що при складанні рівняння коливань у відповіді всі величини, окрім часу, повинні бути представлені в числовому вигляді.
Задача 13.2
Точка здійснює гармонічні коливання. На відстані x1 = 3 см від положення рівноваги її швидкість v1 = 10 см/с, а на відстані x2 = 5 см – швидкість v2 = 6 см/с.
Визначити
циклічну частоту \(\omega\) й амплітуду A коливань.
|
Дано: \(x_{1}\) = 3 см
\(v_{1}\) = 10 см/с
\(x_{2}\) = 5 см
\(v_{2}\) = 6 см/с
|
|
A - ?
\(\omega\) - ?
|
Розв’язання
Припустимо, що рівняння руху точки має вигляд
|
|
\(x=A\sin(\omega{t}+\varphi_{0})\), |
(1) |
де \(\varphi_{0}\) – початкова фаза, t – час. Тоді її швидкість
|
|
\(v_{x}=x^{\prime}(t)=A\omega\cos(\omega{t}+\varphi_{0})\). |
(2) |
Виключимо з рівнянь (1) і (2) час t, скориставшися основною тригонометричною тотожністю \(\sin^{2}\alpha+\cos^{2}\alpha=1\):
|
|
\(\left. \begin{align} \sin(\omega{t}+\varphi_{0})=\frac{x}{A} \\ \cos(\omega{t}+\varphi_{0})=\frac{x}{A\omega} \\ \end{align} \right\} \) \(\Rightarrow\) \(\frac{x^{2}}{A^{2}}+\frac{v^{2}}{A^{2}\omega^{2}}=1\). |
(3) |
(Такий прийом дуже часто використовують в задачах на гармонічні коливання, коли немає необхідності у визначенні моменту часу, або він не заданий в умові задачі).
Записавши вираз (3) для двох випадків (x1, v1, x2, v2), отримаємо систему рівнянь:
\( \left\{ \begin{align} {}x_{1}^{2}+\frac{v_{1}^{2}}{\omega^{2}}=A^{2}; \\ {}x_{2}^{2}+\frac{v_{2}^{2}}{\omega^{2}}=A^{2}. \\ \end{align} \right. \)
Розв’язування цієї системи дає:
\(\omega=\sqrt{\frac{v_{1}^{2}-v_{2}^{2}}{x_{2}^{2}-x_{1}^{2}}}=\sqrt{\frac{100-36}{25-9}}\) = 2 c-1;
\(A=\sqrt{\frac{v_{1}^{2}x_{2}^{2}}{v_{1}^{2}-v_{2}^{2}}}=\sqrt{\frac{100\cdot{25}-36\cdot{9}}{100-36}}=\) 5,83 см.
Задача 13.3
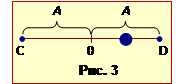 Тіло здійснює гармонічні коливання між точками C і D. Його максимальна швидкість \(v_{m}\) = 10 м/с.
Тіло здійснює гармонічні коливання між точками C і D. Його максимальна швидкість \(v_{m}\) = 10 м/с.
Визначити
середню швидкість \(\langle{v}\rangle\) на шляху від C до D.
|
Дано: \(v_{m}\) = 10 м/с
|
|
\(\langle{v}\rangle\) - ?
|
Розв’язання
Середня шляхова швидкість - це відношення пройденого шляху до часу (див. розділ 1. Кінематика, формула (1.4)):
\(\langle{v}\rangle=\frac{S}{t}\).
Точки C і D максимально віддалені від положення рівноваги (точка O на рис.3), тобто знаходяться на відстані амплітуди від неї, тому шлях точки дорівнює подвоєній амплітуді коливань S = 2A. Якщо припустити, що рух починається в точці C, то за час одного періоду тіло доходить до точки D і повертається в точку C, тому час руху від точки С до точки D дорівнює половині періоду коливань t = T/2, отже:
|
|
\(\langle{v}\rangle=\frac{4A}{T}\). |
(1) |
Максимальна швидкість тіла визначається формулою (13.5б):
\(v_{m}=A\omega=A\cdot\frac{2\pi}{T}\) \(\Rightarrow\) \(T=\frac{2\pi{A}}{v_{m}}\),
де \(\omega\) – кругова (циклічна) частота. Підставивши вираз періоду коливань у формулу (1), остаточно знаходимо:
\(\langle{v}\rangle=\frac{4Av_{m}}{2\pi{A}}=\frac{2v_{m}}{\pi}=\frac{2\cdot{10}}{\pi}\approx\) 6,4 м/с.