ФІЗИКА. Вчимося розв'язувати задачі. "КОЛИВАННЯ ТА ХВИЛІ". Компенсаційний курс
Розділ 13. Механічні коливання
Теоретичні відомості. Найпростіші коливальні системи
|
Найпростішими коливальними системами, в яких можливі вільні гармонічні коливання, є пружинний і математичний маятники. |
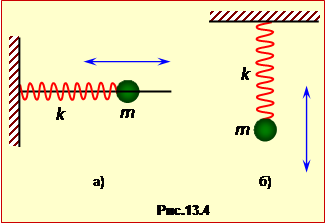 Пружинний маятник являє собою тіло маси m, з'єднане з невагомою пружиною, що має жорсткість k, інший кінець якої закріплений (рис.13.4). За відсутності сил тертя і опору повітря, тобто за умов, коли цими силами можна знехтувати, рух тіла визначається тільки силою пружності
Пружинний маятник являє собою тіло маси m, з'єднане з невагомою пружиною, що має жорсткість k, інший кінець якої закріплений (рис.13.4). За відсутності сил тертя і опору повітря, тобто за умов, коли цими силами можна знехтувати, рух тіла визначається тільки силою пружності
\(F=-kx\),
де x – величина деформації, зумовленої відхиленням тіла від положення рівноваги. Якщо тіло висить на пружині (рис. 13.4б), величина x на включає статичної деформації пружини, створеної вагою вантажу.
Сила пружності задовольняє умові (13.10), тому за відсутності сил тертя і опору пружинний маятник (вантаж на пружині), виведений з положення рівноваги і наданий сам собі, здійснює гармонічні коливання з циклічною частотою
|
|
\(\omega=\sqrt{\frac{k}{m}}\) |
(13.14) |
і періодом
|
|
\(T=2\pi\sqrt{\frac{m}{k}}\), |
(13.15) |
де m – маса маятника, k – жорсткість пружини. Це в однаковій мірі стосується і горизонтальних (рис.13.4а), і вертикальних (рис.13.4б) коливань. Відмінність цих коливань тільки в тому, що в першому випадку в положенні рівноваги пружина недеформована, а в другому – вона розтягнута внаслідок притягання вантажу до Землі.
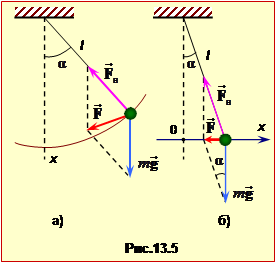
Математичним маятником називається матеріальна точка маси m, підвішена на невагомій нерозтяжній нитці довжиною l (рис.13.5).
За відсутності сил тертя в підвісі і опору середовища рух маятника відбувається тільки під дією сил тяжіння \(m\vec{g}\) і натягу нитки \(\vec{F}_{н}\) (рис.13.5).
Рівнодійна
\(\vec{F}=m\vec{g}+\vec{F}_{н}\)
у загальному випадку складно залежить від кута відхилення нитки \(\alpha\) і зміщення x маятника з положення рівноваги. Тому довільні коливання математичного маятника (рис.13.5а) не є гармонічними. Однак при невеликих амплітудах (\(\alpha\ll{1}\)) \(\mathrm{tg}\alpha=\sin\alpha=\alpha\). Тому можна вважати, що маятник рухається уздовж осі OX під дією рівнодійної сили
\(F_{x}=-mg\cdot\mathrm{tg}\alpha=-mg\alpha\).
З тієї ж причини можна прийняти \alpha=x/l\) (див. рис.13.5б). У результаті одержуємо
\(F_{x}=-kx\),
де x – зміщення маятника з положення рівноваги,
|
|
\(k=\frac{mg}{l}\), |
(13.16) |
Отже, у відповідності до умови (13.10)
|
малі вільні коливання математичного маятника є гармонічними. |
Зіставивши вираз (13.16) з формулами (13.12) та (13.13), знаходимо, що циклічна частота \(\omega\) і період T гармонічних коливань математичного маятника визначається формулами
|
|
\(\omega=\sqrt{\frac{g}{l}}\), |
(13.17) |
і
|
|
\(T=2\pi\sqrt{\frac{l}{g}}\), |
(13.18) |