|
4.43.
|
Яку роботу треба виконати, аби, прикладаючи силу F = 30 H уздовж гладкої похилої площини, витягти брусок маси m = 2 кг на висоту h = 2,5 м з прискоренням a = g?
$\left[ \frac{Fh}{\left( {F}/{mg}\; \right)-1}=150\ Дж \right]$
|
|
4.44.
|
Тіло за 2 с прямолінійно перемістилося на відстань 5 м під дією сили, що змінюється з відстанню, як показано на рис. 4.44. Знайти середню потужність сили за вказаний час. [2 Вт]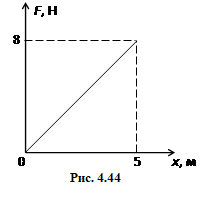
|
|
4.45.
|
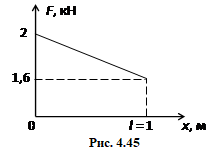 На рис. 4.45 наведено графік залежності сили тиску порохових газів F на снаряд від пройденої ним відстані x у стволі гармати довжиною 1 м. Визначити швидкість снаряду масою 10 кг на момент вильоту з гармати. [600 м/с] На рис. 4.45 наведено графік залежності сили тиску порохових газів F на снаряд від пройденої ним відстані x у стволі гармати довжиною 1 м. Визначити швидкість снаряду масою 10 кг на момент вильоту з гармати. [600 м/с]
|
|
4.46.
|
При пострілі з гвинтівки куля масою 10 г вилітає зі ствола довжиною 1 м із швидкістю 400 м/с. Прийнявши, що сила тиску порохових газів під час руху кулі у стволі лишається сталою, оцінити середню потужність пострілу. [160 кВт]
|
|
4.47.
|
Тролейбус масою 5 т при початковій швидкості 18 км/год і сталій потужності двигуна 50 кВт розганяється до швидкості 28,8 км/год. Знайти прискорення тролейбуса на початку та вкінці розгону. [2 м/с2; 1,25 м/с2]
|
|
4.48.
|
Електровоз, що розвиває потужність 5,4 МВт, рухає потяг масою 2000 т при коефіцієнті опору 0,01. Визначити силу тяги електровоза при швидкості 72 км/год. [470 кН]
|
|
4.49.
|
Наївшись варення, Карлсон піднімався вертикально до своєї хатинки на даху на 4 с довше, ніж зазвичай. Скільки варення з'їв Карлсон, якщо потужність його двигуна складала 50 Вт, а висота даху – 10 м? [2 кг]
|
|
4.50.
|
Тіло масою 1 кг горизонтально кинули з висоти 1 м. Визначити потужність сили тяжіння на момент падіння тіла на землю. [≈45 Вт]
|
|
4.51.
|
Тіло маси m кинули під кутом \(\alpha\) до горизонту з початковою швидкістю v0. Визначити залежність Р(t) потужності сили тяжіння від часу та її середню величину за час польоту. [\(mg(gt-v_{0})\); 0]
|
|
4.52.
|
Гелікоптер масою m, що завис над землею, створює повітряний потік зі швидкістю струменя u. Визначити потужність, яку розвиває двигун. [mgu/2]
|
|
4.53.
|
Який максимальний підйом може подолати потяг масою 2000 т, рухаючися зі швидкістю 7,2 км/год при потужності тепловоза 3700 кВт і силі опору 0,2 % ваги тепловоза. [≈\(4^{\circ}\)]
|
|
4.54.
|
При вимкненому двигуні авто масою 1 т спускається з гори зі сталою швидкістю 54 км/год. При якій корисній потужності на валу двигуна авто зможе з такою самою швидкістю підійматися вгору з уклоном 4 м на 100 м шляху? [12 кВт]
|
|
4.55.
|
На горизонтальній дорозі одне авто із двигуном потужністю 100 кВт може розвивати швидкість до 120 км/год, а інше з двигуном 60 кВт, – до 50 км/год. Із якою максимальною швидкістю вони зможуть рухатися, якщо будуть з'єднані тросом? [78,7 км/год].
|


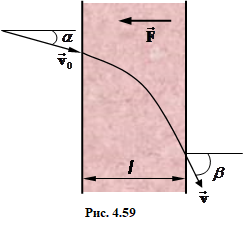 Частинка маси m влітає зі швидкістю
Частинка маси m влітає зі швидкістю