ФІЗИКА. Вчимося розв'язувати задачі. "МЕХАНІКА". Компенсаційний курс
Приклади розв'язування задач
Робота та зміна механічного стану системи
Задача 4.15. Завантажений самоскид рухається прямою горизонтальною дорогою зі швидкістю v = 36 км/год при коефіцієнті опору μ = 0,05. Визначити, на якій відстані S від місця розвантаження водій має вимкнути двигун, аби дістатися туди без використання гальм, і який час Δt для цього знадобиться?
Задача 4.16. Куля перпендикулярно вдаряє в стос міцно закріплених одна за одною однакових дощок. Визначити, в якій за ліком дошці застрягне куля, якщо в першій вона втрачає \(\eta={10}\) % швидкості? Силу опору в дошках уважати незалежною від швидкості кулі.
Задача 4.17. Кулька для пінг-понгу маси m = 20 г вільно падає на підлогу з висоти H = 2 м і пружно (без утрати швидкості) відскакує на висоту h = 1,6 м. Визначити силу опору повітря F, що діє на кульку, вважаючи її сталою.
Задача 4.18. Кульку для пінг-понгу радіуса R = 1,5 см та маси m = 10 г занурили у воду на глибину H = 1м і відпустили. Визначити висоту h, на яку підскочить кулька після спливання. Сили опору (в'язкість) та поверхневий натяг не враховувати. Густина води \( \rho \) = 1 г/см3.
Задача 4.19. Іграшковий електровоз із моторчиком рухається зі швидкістю v горизонтальною коловою колією радіуса R. Визначити, кількість обертів N, яку він зробить по колу до зупинки після вимикання двигуна при коефіцієнті опору μ.
Задача 4.20. Санки довжиною l = 1 м, що рухалися горизонтальною заледенілою дорогою зі швидкістю v = 5 м/с, потрапили на очищену ділянку й зупинилися, коли передній край пройшов по ній шлях S = 2,5 м. Визначити коефіцієнт тертя μ санок об очищену дорогу.
Задача 4.21. Шприц площею перерізу S = 2 см2 і довжиною l = 5 см повністю заповнено водою. Площа перерізу отвору голки S0 = 0,5 мм2. Визначити час τ, за який із шприца випорсне вся вода при прикладанні до поршня сили F = 1,6 Н, уважаючи швидкість струменя сталою. Густина води \( \rho=\) 1 г/см3.
Завантажений самоскид рухається прямою горизонтальною дорогою зі швидкістю v = 36 км/год при коефіцієнті опору μ = 0,05Н.
Визначити,
на якій відстані S від місця розвантаження водій має вимкнути двигун, аби дістатися туди без використання гальм, і який час Δt для цього знадобиться?
|
Дано: v = 36 км/год
μ = 0,05
|
|
S - ? Δt - ? |
Розв'язання
Після вимкнення двигун самоскида на шляху S до місця розвантаження виконує роботу проти сили опору F (рис. 4.15), що дорівнює його початковій кінетичній енергії:
\(8FS=\frac{m{{v}^{2}}}{2}\quad \Rightarrow \quad S=\frac{m{{v}^{2}}}{2S}\).
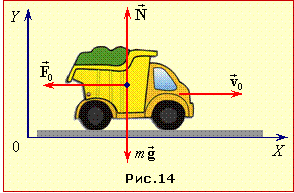
Коефіцієнтом опору називається відношення сили опору до ваги самоскида, тож величина його прискорення при гальмуванні a = μg, і шлях до зупинки
\( {S}=\frac{v^{2}}{2\mu{g}}\) = 100 м.
Час руху до зупинки визначаємо за другим законом Ньютона (2.3):
\(\vec{F}=\frac{\Delta \vec{p}}{\Delta t}\quad \Rightarrow \quad \Delta t=\frac{v}{\mu g}=20\text{ c}\text{.}\)
Куля перпендикулярно вдаряє в стос міцно закріплених одна за одною однакових дощок.
Визначити,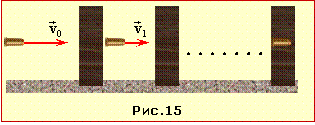
в якій за ліком дошці застрягне куля, якщо в першій вона втрачає \( \eta={10}\) % швидкості? Силу опору в дошках уважати незалежною від швидкості кулі.
|
Дано: η=10% |
|
N - ? |
Розв'язання
За умовою дошки мають однакову товщину, і в кожній на кулю діє однакова сила опору. Тому при пробиванні будь-якої дошки куля втрачає таку саму енергію \( \Delta{W}\), як і в першій дошці:
\( \Delta{W}=\frac{m_{0}^{2}}{2}-\frac{m_{1}^{2}}{2}\),
де m – маса кулі, v0, v1 – швидкість кулі на вльоті та на вильоті з першої дошки, рис. 4.16. Згідно з умовою \( {v}_{1}=(1-\eta)v_{0}\), тому
\( \Delta{W}=\frac{mv_{0}^{2}}{2}\left(1-(1-\eta^{2})\right)\) \( \Rightarrow \) \( \Delta{W}=W_{0}\eta(2-\eta) \),
де \( {W}_{0}\) – початкова кінетична енергія кулі.
Таким чином, кількість пробитих дощок
\( {n}=\frac{W_{0}}{\Delta{W}}=\frac{1}{\eta{(2-\eta)}}\) = 5,26.
Отже, номер дошки, в якій застряне куля,
N = 6.
Кулька для пінг-понгу маси m = 20 г вільно падає на підлогу з висоти H = 2 м і пружно (без утрати швидкості) відскакує на висоту h = 1,6 м.
Визначити
силу опору повітря F, що діє на кульку, вважаючи її сталою.
|
Дано: m = 20 г = 0,02 кг
H = 2 м
h = 1,6 м
|
|
F - ? |
Розв'язання
Унаслідок дії сили опору повітря механічна енергія кульки змінюється на величину роботи цієї сили. В початковому та кінцевому положеннях кулька перебуває в спокої і має лише потенціальну енергію. Тож, прийнявши її рівною нулю на підлозі, маємо:
A = mgh – mgH = mg(h – H).
На від початкового до кінцевого положення кульки S = H + h сила опру виконує роботу A = –F(H + h), отже,
\( {m}g(H-h)=F(H+h)\) \( \Rightarrow \) \( F=\frac{H-h}{H+h}{mg}\) ≈ 2,2 Н.
Кульку для пінг-понгу радіуса R = 1,5 см та маси m = 10 г занурили у воду на глибину H = 1 м і відпустили.
Визначити
висоту h, на яку підскочить кулька після спливання. Сили опору (в'язкість) та поверхневий натяг не враховувати. Густина води \( \rho \) = 1 г/см3.
|
Дано: R = 1,5 см
m = 10 г
H = 1 м = 100 см
\( \rho \) = 1 г/см3
|
|
h - ? |
Розв'язання
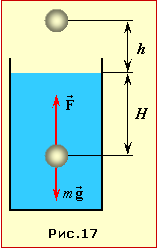
На кульку при спливанні, крім сили тяжіння, на шляху H діє неконсервативна архімедова сила \( \vec{F}\) (рис. 4.18). Згідно із співвідношенням (4.13), її робота на шляху H дорівнює зміні механічної енергії кульки при піднятті на на висоту H + h:
mg(H + h) = FH.
 Виразивши архімедову силу за формулою (6.8) через густину води та радіус кульки, як
Виразивши архімедову силу за формулою (6.8) через густину води та радіус кульки, як
\( {F}=\rho{gV}=\rho\frac{4}{3}\pi{R^{3}}{g}\),
отримаємо:
\( {m}(H+h)=\frac{4\pi{R^{3}\rho{H}}}{3}\) \( \Rightarrow \) \( {h}=H\left(\frac{4\pi{R^{3}\rho}}{3m}-1\right) \) ≈ 41 см.
| Задача 4.18 |
| Задача 4.19 |
Іграшковий електровоз із моторчиком рухається зі швидкістю v горизонтальною коловою колією радіуса R.
Визначити,
кількість обертів N, яку він зробить по колу до зупинки після вимикання двигуна при коефіцієнті опору μ.
|
Дано: v
R
μ
|
|
N - ? |
Розв'язання
На початку гальмування вагончик мав кінетичну енергію \( {W}_{1}=\frac{mv^{2}}{2}\), яка надалі зменшилася до нуля (\( {W}_{1}={0}\)) за рахунок роботи A сили опору. Позаяк при русі горизонтальною поверхнею потенціальна енергія вагончика не змінюється, то
\( \Delta{W}=-\frac{mv^{2}}{2}=-F\cdot{S}\) \( \Rightarrow \) \( \frac{mv^{2}}{2}={FS}\),
де F - сила опору, S - пройдений вагончиком шлях, який пов'язаний з кількістю обертів по колу очевидним співвідношенням \( {S}=2\pi{RN}\). Таким чином,
\( {N}=\frac{mv^{2}}{4\pi{RF}}\).
Сила опору \( {F}=\mu{N}=\mu{mg}\), отже
\( {N}=\frac{v^{2}}{4\pi\mu{Rg}}\).
Задача 4.20.
Санки довжиною l = 1 м, що рухалися горизонтальною заледенілою дорогою зі швидкістю v = 5 м/с, потрапили на очищену ділянку й зупинилися, коли передній край пройшов по ній шлях S = 2,5 м. Визначити
коефіцієнт тертя μ санок об очищену дорогу.
|
Дано: \( {l}\)=1 м
v = 5 м/с
S = 2,5 м
|
|
\( \mu \) - ? |
Розв'язання
Крім сили тертя на санки діють сила тяжіння та сила нормальної реакції дороги Однак останні дві сили роботи не виконують, тому зміна кінетичної енергії санок при гальмуванні на асфальті зумовлена тільки роботою сили тертя:
| \( \Delta{W}_{к}=A_{т}\) \( \Rightarrow \) \( {-}\frac{mv^{2}}{2}=A_{т}\) \( \Rightarrow \) \( \frac{mv^{2}}{2}=|A_{т}| \) | (1) |
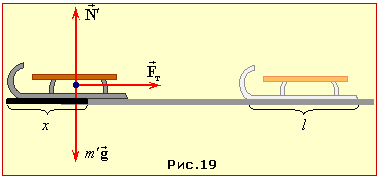 У процесі гальмування, доки санки не повністю виїхали на асфальт, сила тертя є змінною, позаяк частина санок, яка знаходиться на асфальті, поступово збільшується. Величина сили тертя \( {F}_{т}=\mu{N}=\mu{m^{\prime}}g\), де \( \mu \) – шуканий коефіцієнт тертя, а \( {m^{\prime}}\) – маса частини санок, що вже виїхала на асфальт (рис. 4.20). Очевидно, що \( {m}^{\prime}=(m/l){x}\), де \( {l}\) – довжина санок, а x - довжина їхньої частини, що знаходиться на асфальті. Отже \( {F}_{т}(x)=\frac{\mu{mg}x}{l}\), \( {x}\le{l}\).
У процесі гальмування, доки санки не повністю виїхали на асфальт, сила тертя є змінною, позаяк частина санок, яка знаходиться на асфальті, поступово збільшується. Величина сили тертя \( {F}_{т}=\mu{N}=\mu{m^{\prime}}g\), де \( \mu \) – шуканий коефіцієнт тертя, а \( {m^{\prime}}\) – маса частини санок, що вже виїхала на асфальт (рис. 4.20). Очевидно, що \( {m}^{\prime}=(m/l){x}\), де \( {l}\) – довжина санок, а x - довжина їхньої частини, що знаходиться на асфальті. Отже \( {F}_{т}(x)=\frac{\mu{mg}x}{l}\), \( {x}\le{l}\).
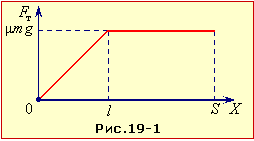
Після того, як санки повністю виїдуть на асфальт (\( {x}\ge{l}\)), сила тертя стає рівною \( \mu{mg}\) і надалі не змінюється. Отже графік сили тертя має вигляд рис. 4.20-1. Як сказано в теорії (п. 4.1), площа під ним чисельно дорівнює модулю роботи сили тертя:
\( {|A_{т}|}=\frac{1}{2}(S+S-l)\mu{mg}=\frac{\mu{mg}(2S-l)}{2}\).
 Підставивши цей вираз у формулу (1), дістанемо
Підставивши цей вираз у формулу (1), дістанемо
\( \mu=\frac{v^{2}}{g(2S-l)}={0,64}\).
| Задача 4.20 |
| Задача 4.21 |
Шприц площею перерізу S = 2 см2 і довжиною l = 5 см повністю заповнено водою. Площа перерізу отвору голки S0 = 0,5 мм2.
Визначити
час τ, за який із шприца випорсне вся вода при прикладанні до поршня сили F = 1,6 Н, уважаючи швидкість струменя сталою. Густина води \( \rho=\) 1 г/см3.
|
Дано: S = 2 см2
l = 5 см
S0 = 0,5 мм2
F = 1,6 Н
ρ = 1 г/см3
|
|
τ–? |
Розв'язання
Початковий об'єм води у шприці V = lS. Якщо позначити об'єм води, що виходить із шприца за одиницю часу, як v, то час витікання всієї води
|
$\tau =\frac{V}{v}$. |
(1) |
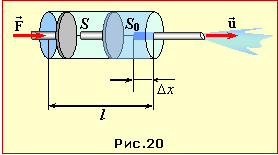 Для визначення величини v виділимо тонкий шар води об'ємом \( \Delta{V}=S_{0}\Delta{x}\), що прилягає до отвору голки, рис. 4.21. Ця вода при швидкості руху частинок u пройде крізь отвір за час
Для визначення величини v виділимо тонкий шар води об'ємом \( \Delta{V}=S_{0}\Delta{x}\), що прилягає до отвору голки, рис. 4.21. Ця вода при швидкості руху частинок u пройде крізь отвір за час
$\Delta t=\frac{\Delta x}{u}$,
отже,
$v=\frac{\Delta V}{\Delta t}={{S}_{0}}u$
Підставивши цей вираз у формулу (1), отримаємо
| \( \tau=\frac{lS}{S_{0}u}\). | (2) |
Відтак задача зводиться до визначення швидкості струменя u, яку легко знайти за допомогою енергетичних міркувань. А саме. Кожна частинка води набуває швидкості u і відповідної кінетичної енергії завдяки роботі сили тиску F на поршень та воду. Тож за теоремою про кінетичну енергію (4.4)
\( {Fl}=\frac{mu^{2}}{2}\),
де m – початкова маса води в шприці. Позаяк \( {m}=\rho{lS}\), то
\( {Fl}=\frac{\rho{S}lu^{2}}{2}\) \( \Rightarrow \) \( {u}=\sqrt{\frac{2F}{\rho{S}}}\).
Підставивши цей результат у вираз (2), отримуємо відповідь:
\( \tau=\frac{lS}{S_{0}}\sqrt{\frac{\rho{S}}{2F}}\) τ = 5 с.
.