ФІЗИКА. Вчимося розв'язувати задачі. "МЕХАНІКА". Компенсаційний курс
Приклади розв'язування задач
Визначення роботи через механічну енергію
Задача 4.4. Однорідний циліндричний стовб масою m і довжиною l лежить на землі. Визначити роботу A, яку треба виконати, аби поставити його вертикально.
Задача 4.5. При розтяганні недеформованої пружини виконано роботу A1 = 5 Дж. Визначити роботу A2, яку додатково слід виконати, аби видовжити пружину ще на η = 20% початкового розтягу.
Задача 4.6. Циліндричний колодязь діаметром d = 1,5 м та глибиною H = 20 м наполовину заповнено водою (\( \rho={1}\) г/см3). Визначити роботу A, яку має виконати електрична помпа, аби викачати всю воду з колодязя. Кінетичну енергією води та втрати в помпі не рахувати.
Задача 4.7. Авто масою m = 1 т спускається з вимкненим двигуном із вершини гори висотою h = 100 м і, пройшовши якийсь шлях по горизонталі, зупиняється. Визначити роботу A, що її має виконати двигун, аби авто повернулося назад шляхом спуску.
Задача 4.8. Кульку масою m = 10 г, яка висить на нитці довжиною l = 1 м, розкручують у горизонтальній площині так, що нитка відхиляється від вертикалі на кут φ = 10°. Визначити роботу A по розкручуванню кульки.
Задача 4.9. Прийнявши радіус Землі R = 6400 км, знайти відношення робіт (A2/A1) необхідних, аби підняти тіло на висоту h = 3200 км над поверхнею Землі (A1) та вивести його на колову орбіту такої самої висоти (A2).
Задача 4.10. Довести, що формула потенціальної енергії тіла біля поверхні планети (Wп = mgh) є:
1) окремим випадком загальної формули (4.6);
2) придатною для тіла довільних розмірів і форми, де h – висота розташування його центра мас.
| дача 4.3 |
| Задача 4.4 |
Однорідний циліндричний стовб масою m і довжиною l лежить на землі.
Визначити
роботу A, яку треба виконати, аби поставити його вертикально.
|
Дано: m, l |
|
A - ? |
Розв'язання
Ця задача змістовно є подібною до задачі 4.3. Але розв'язувати її через пряме обчислення немає потреби, позаяк робота проти сили тяжіння при підніманні стовба дорівнює зміні його потенціальної енергії (див. п.п. 4.1, 4.2). Тож, прийнявши її в початковому положенні стовба за нуль і врахувавши, що його центр мас знаходиться посередині, одразу дістанемо відповідь:
\( {A}=\frac{1}{2}{mgl}\).
Зверніть увагу на ефективність і простоту "енергетичного" способу розв'язання, при якому задача фактично є усною.
| Задача 4.4 |
| Задача 4.5 |
При розтяганні недеформованої пружини виконано роботу A1 = 5 Дж.
Визначити
роботу A2, яку додатково слід виконати, аби розтягти пружину ще на η = 20% від початкового видовження.
|
Дано: A1 = 4 Дж η = 20% |
|
А2 - ? |
Розв'язання
Робота по розтяганню пружини йде на зміну її потенціальної енергії. Тож, оскільки потенціальна енергія не розтягненої пружини Wп0 = 0, початкова робота, згідно з виразами (4.5) і (4.8), дорівнює
|
\( {A}_{1}=W_{п1}=\frac{kx_{1}^{2}}{2}\), |
(1) |
де k – жорсткість пружини, x1 – її початковий розтяг.
Робота, потрібна для додаткового розтягання пружини, дорівнює:
|
\( {A}_{2}=W_{п2}-W_{п1}\) = $\frac{k}{2}\left( x_{2}^{2}-x_{1}^{2} \right)$, |
(2) |
де кінцеве видовження пружини за умовою складає
х2 = х1 +ηх1 = (1 + η)х1.
Відтак підставивши цю величину у вираз (2) і врахувавши вираз (1), після елементарних викладок отримаємо наступну відповідь:
А2 = 2(2 + η)А1 = 2,2 Дж.
| Задача 4.5 |
| Задача 4.6 |
Циліндричний колодязь діаметром d = 1,5 м та глибиною H = 20 м наполовину заповнено водою (\( \rho={1}\) г/см3).
Визначити
роботу A, яку має виконати електрична помпа, аби викачати всю воду з колодязя. Кінетичну енергією води та втрати в помпі не рахувати
|
Дано: d = 1,5 м
H = 20 м
\( \rho={1}\) г/м3
|
|
A - ? |
Розв'язання
 Робота помпи йде на збільшення потенціальної енергії води:
Робота помпи йде на збільшення потенціальної енергії води:
A = Wп2 – Wп1.
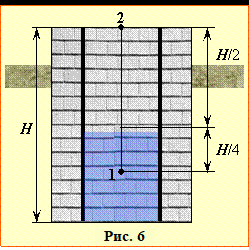
Приймемо за нульовий рівень горизонтальну площину, що проходить через центр мас води перед початком відкачування (т. 1 на рис. 6), тоді Wп1 = 0. У процесі відкачування помпа кожну частинку, тож і всю воду, підіймає до рівня 2, що розташований на висоті \( {h}=\frac{3H}{4}\) від початкового положення центра мас води і надає їй потенціальної енергії Wп2 = mgh. Отже,
\( {A}=\frac{3mgH}{4}\).
Маса води в колодязі \( {m}=\frac{\rho{S}H}{2}=\frac{\pi{d}^{2}\rho{H}}{8}\), таким чином корисна робота насоса, котру треба знайти, дорівнює
\( {A}=\frac{3\pi{d^{2}}\rho{g}H^{2}}{32}\) = 2,6 МДж.
| Задача 4.6 |
| Задача 4.7 |
Авто масою m = 1 т спускається з вимкненим двигуном із вершини гори висотою h = 100 м, і пройшовши якийсь шлях по горизонталі, зупиняється.
Визначити
роботу A, що її має виконати двигун, аби авто повернулося назад шляхом спуску.
|
Дано: m = 1000 кг
h = 100 м
|
|
A - ? |
Розв'язання
На спуску авто за рахунок своєї потенціальної енергії виконує роботу А′ проти сил тертя та опору, отже
А′ = mgh.
Ту саму роботу проти сил тертя та опору на підйомі має виконати двигун. Але він має ще й надати автомобілю потенціальної енергії W = mgh. Отже, повна робота двигуна складає
А = 2mgh.
| Задача 4.7 |
| Задача 4.8 |
Кульку масою m = 10 г, яка висить на нитці довжиною l = 1 м, розкручують у горизонтальній площині так, що нитка відхиляється від вертикалі на кут φ = 10°.
Визначити
роботу A по розкручуванню кульки.
|
Дано: m = 10 г l = 1 м φ = 10°
|
|
A - ? |
Розв’язання
При розкручуванні кулька піднімається на деяку висоту h над початковим рівнем і набуває певної швидкості v, рис. 8. При цьому змінюються її кінетична Wк, потенціальна Wп та повна механічна енергія W. Згідно із виразом (4.13), зміна повної енергії кульки \( \Delta{W}\) дорівнює роботі по розкручуванню:
| \( {A}=\Delta{W}=\Delta{W}_{п}+\Delta{W}_{к}=mgh+\frac{mv^{2}}{2}\) | (1) |
Таким чином, задача зводиться до визначення швидкості кульки v та висоти підйому h .
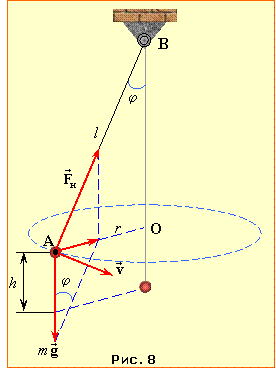
З рис. 4.8 видно, що
\( {h=AB-OB}=l-l\cos\varphi=2l\sin^{2}\left(\frac{\varphi}{2}\right) \).
Для малих кутів (виражених в радіанах) sinφ = φ, тож
|
$h=\frac{l{{\varphi }^{2}}}{2}$. |
(2) |
Рух кульки по коловій траєкторії відбувається під дією рівнодійної сил тяжіння \( {m}\vec{g}\) та натягу нитки ${{\vec{F}}_{н}}$, що визначається, як
\( {F}=mg\mathrm{tg}\varphi=mg{\varphi}\).
З іншого боку, ${{F}_{\text{н}}}=\frac{m{{v}^{2}}}{r}$ (формули (2.5) та (1.28)), отже
| \( {m}g\varphi=\frac{mv^{2}}{r}\); \( \Rightarrow \) \( {v}^{2}=gr\varphi \). | (3) |
Із рис. 4.8 видно, що \( {r}=l\sin\varphi=l\varphi \), тож
\( {v}^{2}=gl\varphi^{2}\).
Відтак підставивши вирази h (2) і v2 (3) у формулу (1), визначимо роботу розкручування:
\( {A}=mg\frac{l\varphi^{2}}{2}+mg\frac{l\varphi^{2}}{2}=mgl\varphi^{2}\),
і, (виразивши величину φ в радіанах), знайдемо числову відповідь:
А = 0,003 Дж = 3 мДж.
| Задача 4.9. |
| Задача 4.9 |
Прийнявши радіус Землі R = 6400 км,
визначити
відношення робіт (A2/A1), які треба виконати, аби підняти тіло на висоту h = 3200 км над поверхнею Землі (A1) та вивести його на колову орбіту такої самої висоти (A2).
|
Дано: h = 3200 км
R = 6400 км
|
|
(A2/A1) - ? |
Розв'язання
Мінімальна робота, потрібна для підйому тіла на якусь висоту, дорівнює зміні його потенціальної енергії: A = Wп2 – Wп1. При підйомі на вказану в умові висоту сила тяжіння та прискорення g помітно змінюються. Тож зміна потенціальної енергії тіла маси m визначається формулою (4.10):
\( {A}=G\frac{Mm}{r_{1}}-G\frac{Mm}{r_{2}}\),
де M – маса Землі, а r – відстань від тіла до центра Землі. У вихідному положенні тіло знаходилось на поверхні Землі, тому r1 = R. У кінцевому положенні r2 = R + h. Отже,
| \( {A}_{1}=GMm\left(\frac{1}{R}-\frac{1}{R+h}\right)=GMm\frac{h}{R(R+h)}\). | (1) |
При виведенні на колову орбіту тілу, крім зміни потенціальної енергії, треба надати необхідну орбітальну швидкість і кінетичну енергію. Тож робота по виведенню тіла на орбіту складає
| \( {A}_{2}=A_{1}+\frac{mv^{2}}{2}\). | (2) |
Орбітальну швидкість супутника визначимо за допомогою другого закону Ньютона \( {F}=ma \), де \( {F}=G\frac{Mm}{(R+h)^{2}}\) , і \( {a}=\frac{v^{2}}{R+h}\) – доцентрове прискорення на орбіті радіуса r2 = R + h. Отже,
\( {G}\frac{Mm}{(R+h)^{2}}=\frac{mv^{2}}{(R+h)}\) \( \Rightarrow \) \( {m}v^{2}=G\frac{Mm}{R+h}\).
Підставивши це значення в формулу (2), отримаємо:
\( {A}_{2}=A_{1}+\frac{FMm}{2(R+h)}\),
а для відношення робіт
\( \frac{A_{2}}{A_{1}}=1+\frac{GMm}{2(R+h)A_{1}}\)
і, підставивши вираз (1), знайдемо відповідь:
\( \frac{A_{2}}{A_{1}}=1+\frac{R}{2h}={2}\).
| Задача 4.10. |
|||
| Задача 4.10. | |||
|
Довести, що формула потенціальної енергії тіла біля поверхні планети (Wп = mgh) є: 1) окремим випадком загальної формули (4.6); 2) придатною для тіла довільних розмірів і форми, де h – висота розташування його центра мас.
Доведення 1). При піднятті тіла масою m з поверхні планети маси M і радіуса R на висоту h зміна його потенціальної енергії згідно з виразом (4.6) складає Wп – Wп0 = $GmM\left( \frac{1}{R}-\frac{1}{R+h} \right)=\frac{GMmh}{R\left( R+h \right)}$ і не залежить від положення нульового рівня потенціальної енергії (див. п. 4.2). Але, позаяк при його виборі на поверхні планети Wп0 = 0, отриманий вираз визначає саму потенціальну енергію тіла на висоті h. Перепишемо його у вигляді
і, врахувавши вираз (2.9) та те, що біля поверхні планети величина h у формулі (1) є неістотною, отримаємо ${{W}_{п}}=mgh$, що й було треба. 2). Потенціальна енергія довільного тіла у полі сил тяжіння складається з потенціальних енергій всіх його частин: ${{W}_{\text{}}}=\sum{\Delta {{W}_{i}}}$. Тому, якщо тіло подумки поділити на гранично вузькі горизонтальні смужки масами Δmi, (одну з них показано на рис. 4.10), то ${{W}_{\text{п}}}=g\sum{{{m}_{i}}{{h}_{i}}}$, де hi – висота розташування смужки відносно нульового рівня. Відтак помноживши й поділивши цей вираз на масу всього тіла, отримаємо: ${{W}_{\text{п}}}=mg\frac{\sum{{{m}_{i}}{{h}_{i}}}}{m}$, або, з урахуванням виразу (3.6а), ${{W}_{\text{п}}}=mgh$, де h = Yс – вертикальна координата центра мас тіла.
|