ФІЗИКА. Вчимося розв'язувати задачі. "МЕХАНІКА". Компенсаційний курс

Короткі теоретичні відомості

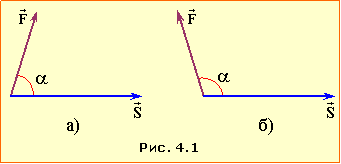
4.1. Робота сили

Якщо на рухоме тіло діє сила, то вона виконує механічну роботу. За означенням

роботою A сталої сили $ \vec{F}$ на переміщенні $ \vec{S}$ називається величина, що дорівнює скалярному добутку цих векторів (рис. 4.1):

${A }=\vec{F}\cdot\vec{S}=F{S}\cos\alpha $.

(4.1)

Отже, можна сказати, що робота є мірою дії сили на заданому переміщенні. Наголосимо: переміщенні, а не шляху. Виняток становить лише прямолінійний рух уздовж лінії дії сили, коли величина переміщення збігається із пройденим шляхом, і робота дорівнює

$A=\pm F\cdot S$

(4.1а)

Робота є скалярною алгебраїчною величиною, знак якої визначається напрямом прикладеної сили відносно напрямку руху. Зокрема, сила, що діє перпендикулярно до переміщення (α = 90°), роботи не виконує (A = 0), а при α > 90° (рис. 4.1б), робота сили є від'ємною, й сила не сприяє переміщенню тіла, а гальмує його. В такому випадку буває зручніше говорити не про від'ємну роботу даної сили, а про додатню роботу А′ = – А тіла проти цієї сили. Відмітимо також, що п

Слід також розуміти, що термін "робота" відображає не властивість чи стан, а процес. Вона не "міститься" в чомусь, а виконується, тож вислів "кількість роботи" є некоректним.

Одиницею роботи є джоуль (Дж), 1 Дж = 1 Н·м – робота, що виконується сталою силою 1 Н на переміщенні 1 м, за умови, що сила діє в напрямку переміщення (α = 0°).

Робота рівнодійної декількох сил $ \vec{F}=\sum\vec{F}_{i}$ на даному переміщенні $ \vec{S}$ дорівнює алгебраїчній сумі робіт кожної зі складових сил:

$ {A}=\vec{F}\cdot\vec{S} $ = $ \left(\sum\vec{F}_{i}\right)\vec{S} $ = $ \sum(\vec{F}_{i}\vec{S}) $ $ \Rightarrow $ $A=\sum{\Delta {{A}_{i}}}$.

(4.2)

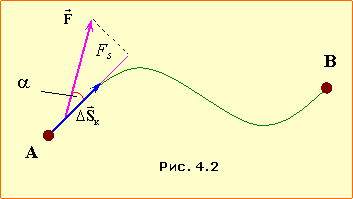
При дії довільної сили на тіло, що рухається по довільній траєкторії, величина F та кут α у процесі руху змінюються. При цьому, позаяк загальне переміщення тіла між двома точками (рис. 4.2) складається з переміщень $\Delta {{\vec{S}}_{k}}$ на окремих ділянках, робота змінної сили на заданому шляху дорівнює сумі робіт ΔA_k на всіх його ділянках:

$A=\sum{\Delta {{A}_{k}}}$

(4.2а)

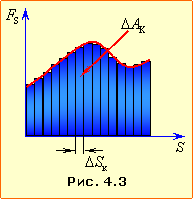
Обчислення роботи змінної сили виконуються за допомогою методів вищої математики. Але при якісному аналізі, а інколи й у розрахунках, може стати в пригоді графік залежності проєкції сили F_s від пройденого шляху S, рис. 4.3. А саме. Якщо всю траєкторію подумки розбити на дуже малі ділянки, так, щоби силу F та кут α можна було вважати незмінними, то на кожній ділянці елементарна робота ΔA_k ≈ F_s·S_k чисельно дорівнюватиме площі відповідної смужки на графіку, і згідно з виразом (4.2а), вся робота наближено дорівнює площі площі зафарбованої уступчастої фігури на рис. 4.3.

Аби отриманий у такий спосіб результат був точним, смужки мають бути гранично вузькими ($\Delta{S}_{k}\to{0}$). В такому разі ламана на рис. 4.3 зливається з графіком F_S = f(S) , тож

робота змінної сили на заданому шляху чисельно дорівнює площі під відповідною ділянкою графіка сили.

Проте слід зауважити, що точне обчислення цієї площі, знову таки вимагає застосування вищої математики і взагалі не завжди є можливим. Виняток становить тільки лінійна залежність F_S(S), коли задана ділянка графіка разом з осями утворює звичайну трапецію чи трикутник.