ФІЗИКА. Вчимося розв'язувати задачі. "МЕХАНІКА". Компенсаційний курс
Приклади розв’язування задач
Рівномірний рух по колу
У задачах на рівномірний рух по колу одним з найважливіших етапів розв'язування є аналіз того, які взаємодії даного тіла з іншими створюють "доцентрову силу", та складання рівняння руху за другим законом Ньютона.
При рівномірному русі тіла по колу напрямки сил, що діють на нього, прискорень та швидкостей неперервно змінюються. Тому використовувати при розв'язуванні нерухому систему відліку із фіксованим напрямком координатних осей є незручно. Набагато краще розглядати рух в кожен момент у проєкціях на радіус колової траєкторії та (при необхідності) на якийсь інший зручний напрямок, приміром, дотичну до траєкторії.
Задача 2.16. Літак виконує "мертву петлю", рухаючись зі сталою швидкістю у вертикальній площині по коловій траєкторії радіуса R = 1 км. Визначити швидкість v літака, якщо в ньому максимальна вага пілота в \( \eta={3}\) рази перевищує мінімальну.
Задача 2.17. На трасі мотокросу спортсмен долає пагорб у вигляді сферичного купола радіусом R = 40 м. Визначити, при якій найменшій швидкості \( {v}_{min}\) мотоцикл на вершині пагорба відірветься від землі.
Задача 2.18. Маленьку кульку, підвішену на нитці довжини l, рівномірно обертають у горизонтальній площині по колу радіусом R << l. Визначити період обертання кульки T.
Задача 2.19. Байкер рухається по коловому треку з кутом нахилу полотна до горизонту α = 15°. Максимальний радіус треку R = 50 м, коефіцієнт тертя між колесами та покриттям треку μ = 0,6. Визначити: 1. Максимальну швидкість \( {v}_{m}\), яку може розвинути байкер. 2. Кут \( \vartheta \), на який він має відхилятися від вертикалі, аби не впасти.
Задача 2.20. Вага тіла на полюсі планети є на η = 5% більша, ніж на екваторі. Визначити середню густину речовина планети ρ, якщо тривалість доби на ній складає T = 10 год.
| Задача 2.16 |
| Задача 2.16 |
Літак виконує "мертву петлю", рухаючись зі сталою швидкістю у вертикальній площині по коловій траєкторії радіуса R = 1 км.
Визначити
швидкість v літака, якщо в ньому максимальна вага пілота в \( \eta={3}\) рази перевищує
мінімальну.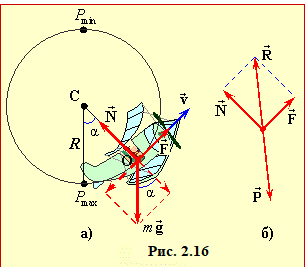
|
Дано: R = 1 км η = 3 |
|
v - ? |
Розв'язання
На рис. 2.16а схематично показано сили, що діють на пілота в літаку: сила тяжіння \( {m}\vec{g}\) та спрямована до центра траєкторії сила тиску сидіння \( \vec{N}\) і перпендикулярна до неї сила тиску спинки крісла \( \vec{F}\), що разом створюють силу реакції опори \(\vec{F}_{\text{оп}} = \vec{N} + \vec{F}\), рис. 2.16б. За третім законом Ньютона вага пілота (сила тиску на крісло) \(\vec{P} = – \vec{F}_{\text{оп}}\) і має модуль
| \( {P}=\sqrt{N^{2}+F^{2}}\). | (1) |
Далі, аби врахувати задану величину η, слід визначити сили N і F. Для цього запишемо другий закон Ньютона (2.5)
| \( {m}\vec{g}+\vec{N}+\vec{F}=m\vec{a}\) | (2) |
і врахуємо, що швидкість літака v = const, тож прискорення \( \vec{a}\) є доцентровим, тобто спрямоване радіально і має величину \( {a}=\frac{v^{2}}{R}\). В такому разі, записавши рівняння (2) у проєкціях на радіус та на дотичну до траєкторії, отримаємо:
| \( {N}=\frac{mv^{2}}{R}+mg\cos\alpha \), | ||
| \( {F}=mg\sin\alpha \). |
Звідси, згідно з (1), маємо:
| \( {P}=\sqrt{{{\left( \frac{m{{v}^{2}}}{R}+mg\cos \alpha \right)}^{2}}+{{\left( mg\sin \alpha \right)}^{2}}}\) |
і, після розкриття дужок,:
\( {P}=\sqrt{\left(\frac{mv^{2}}{R}\right)^{2}+(mg)^{2}+2\frac{m^{2}gv^{2}}{R}\cos\alpha}\).
Максимальній та мінімальній вазі пілота відповідають значення cosα = ±1 (нижня та верхня точки траєкторії) і величини:
| \(\left\{ \begin{matrix} {{P}_{\max }}=\frac{m{{v}^{2}}}{R}+mg, \\ {{P}_{\min }}=\frac{m{{v}^{2}}}{R}-mg. \\\end{matrix} \right.\) | (3) |
Відтак, поділивши праві та ліві частини цих виразів і врахувавши умову \( {P}_{max}/P_{min}=\eta \), після нескладних перетворень знайдемо:
\( {v}=\sqrt{\frac{\eta+1}{\eta-1}gR}= {504}\) км/год.
Із другого рівняння (3) випливає, що при швидкості літака
| \( {v}=\sqrt{gR}\) = 360 км/год, | (4) |
вага пілота у верхній точці траєкторії дорівнює нулю, тобто він перебуває в стані невагомості.
| Задача 2.17 |
| Задача 2.17 |
На трасі мотокросу спортсмен долає пагорб у вигляді сферичного купола радіусом R = 40 м.
Визначити,
при якій найменшій швидкості \( {v}_{min}\) мотоцикл на вершині пагорба відірветься від землі.
|
Дано: R = 40 м |
|
vmin - ? |
Розв'язання
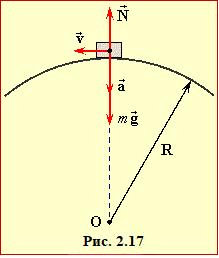
Вершину пагорба мотоцикліст проходить із доцентровим прискоренням a = (v2/R), що створюється силою тяжіння \( {m}\vec{g}\) та протилежно спрямованою реакцією опори \( \vec{N}\) (рис. 2.17). Тож за другим законом Ньютона (2.5)
| \( {mg}-N=\frac{mv^{2}}{R}\). | (1) |
Звідси випливає, що при збільшенні швидкості сила N, тож і сила тиску на пагорб (вага мотоцикла зі спортсменом), зменшуються і при певній величині vmin набувають нульового значення. А це означає, що мотоцикл відривається від землі. Таким чином, поклавши N = 0 в рівнянні (1), отримаємо
\( {mg}=\frac{mv_{min}^{2}}{R}\) \( \Rightarrow \)
|
${{v}_{\min }}=\sqrt{gR}$ |
(2) |
Обчислення дає:
vmin= 20 м/с = 72 км/год.
У момент відриву мотоцикл із мотоциклістом перестають тиснути на опору, тобто переходять у стан невагомості, як і пілот у попередній задачі при проходженні верхньої точки траєкторії.
| Задача 2.18 |
| Задача 2.18 |
Маленьку кульку, підвішену на нитці заданої довжини l, рівномірно обертають у горизонтальній площині по колу радіусом R<<l.
Визначити
період обертання кульки T.
|
Дано: l |
|
Т - ? |
Розв'язання
При рівномірному русі кульки із швидкістю v по колу радіуса R період обертання дорівнює
| \( {T}=\frac{2\pi{R}}{v}\), | (1) |
Кулька рухається під дією сил тяжіння \( {m}\vec{g}\) та натягу нитки \( \vec{F}_{\text{н}}\), рівнодійна яких \(\vec{F}\) має модуль F = mgtgφ (рис. 2.18) і створює прискорення a = gtgφ. Це прискорення є доцентровим і визначається формулою (1.28), отже
| g·tgφ = \( \frac{v^{2}}{R}\). | (2) | |
Позаяк за умовою R<<l, кут φ є малим, тож у виразі (2) можна покласти tgφ = (R/l). Тоді
\(\frac{gR}{l}=\frac{{{v}^{2}}}{R}\) \( \Rightarrow \) \(v=R\sqrt{\frac{g}{l}}\),
І з виразу (1) випливає наступна відповідь:
|
\(T=2\pi \sqrt{\frac{l}{g}}\). |
Отриманий вираз збігається з формулою періоду малих коливань математичного маятника, а нитка описує конус. Тому кульку на нитці, що обертається по колу в горизонтальній площині, називають конічним маятником.
| Задача 2.19 |
| Задача 2.19 |
Байкер рухається по коловому треку з кутом нахилу полотна до горизонту α = 15°. Максимальний радіус треку R = 50 м, коефіцієнт тертя між колесами та покриттям треку μ = 0,6.
Визначити:
1. Максимальну швидкість \( {v}_{m}\), яку може розвинути байкер.
2. Кут \( \vartheta \), на який він має відхилитися від вертикалі, аби не впасти.
|
Дано: α = 15° μ = 0,6 R = 50 м |
|
vm - ? η - ? |
Розв'язання
1. На байк діють сили тяжіння \( {m}\vec{g}\) (m – сумарна маса) і нормальної реакції опори \( \vec{N}\) та поперечна сила тертя\( \vec{F}\), що утримує його на коловій траєкторії, рис. 2.19a. (Діє ще й не показана поздовжня сила тертя, що є силою тяги і для розв'язування задачі не потрібна).
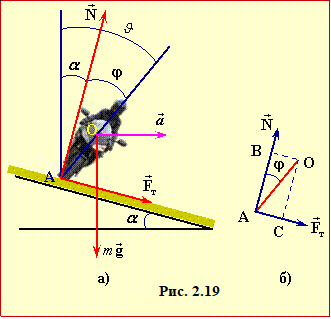
Під дією вказаних сил байк в горизонтальній площині по колу з доцентровим прискоренням \( \vec{a}\), модуль якого визначається швидкістю байка та радіусом траєкторії, як \( {a}=v^{2}/r\), (Розділ 1, ф-ла (1.28)). Отже, за ІІ законом Ньютона
\( {m}\vec{g}+\vec{N}+\vec{F}=m\vec{a}\),
і в проєкціях на осі координат
| \(\left\{ \begin{matrix} N\sin \alpha +{{F}}\cos \alpha =\dfrac{m{{v}^{2}}}{r},\ \ \ \ \ \\ -mg-{{F}}\sin \alpha +N\cos \alpha =0. \\\end{matrix} \right.\) | (1) |
Із першого рівняння системи випливає, що максимальна можлива швидкість руху байка без зісковзування vm відповідає радіусу траєкторії r = R і максимальній можливій силі тертя спокою F = μN (див. п. 2.3). Підставивши ці вирази в рівняння (1), отримаємо:
\(\left\{ \begin{matrix} N\left( \sin \alpha +\mu \cos \alpha \right)=\dfrac{mv_{m}^{2}}{R} \\ N\left( \cos \alpha -\mu \sin \alpha \right)=mg.\ \ \ \\\end{matrix} \right.\),
Звідси після нескладних перетворень знайдемо:
| \( {v}_{m}=\sqrt{gR\frac{\mathrm{tg}\alpha+\mu}{1-\mu\mathrm{tg}\alpha}}\). | (2) |
Обчислення дають:
vm = 22,75 м/с ≈ 82 км/год.
2. При знайденій швидкості байк буде рухатися без проковзування. Але лише лише цього для стійкого положення байкера на траєкторії є замало. З рис. 19б видно, що відносно центра ваги системи О сили \( \vec{N}\) і \( \vec{F}\) створюють обертові моменти протилежного знаку (див. Розділ 5). Тому при довільному куті відхилення від вертикалі байкера буде "завалювати" в той, чи інший бік. Тож він, аби не впасти, має відхилятися від вертикалі на такий кут \( \vartheta \) = α + φ, при якому вказані моменти мають однакову величину, отже,
| Nl1 = Fl2 \( \Rightarrow \) $\frac{F}{N}=\dfrac{{{l}_{1}}}{{{l}_{2}}}=\operatorname{tg}\varphi $ |
Позаяк при швидкості vm сила F = μN, то tgφ = μ, і необхідний кут відхилення байкера від вертикалі при максимальній швидкості руху складає:
| \( \vartheta=\alpha+\varphi=\alpha+\mathrm{arctg}\mu \). |
(3) |
Обчислення дають:
\( \vartheta=15^{\circ}+\mathrm{arctg}0,6=46^{\circ}\).
Таким чином, одночасне виконання умов (2) і (3) забезпечує рух байкера без падіння, а максимальна можлива швидкість визначається параметрами треку та коефіцієнтом тертя μ між шинами байка та полотном треку. При цьому існує два граничні випадки:
а). Полотно треку горизонтальне (\( \alpha={0}\)). В такому разі максимальна швидкість складає \( {v}_{m}=\sqrt{\mu{gR}}={17}\) м/с і суттєво поступається знайденій вище величині. Саме тому для покращення швидкісних характеристик треку полотно роблять похилим.
б). Коли величина \( \mu\mathrm{tg}\alpha \) у формулі (2) наближається до одиниці, а кут \( \alpha \) — до значення \( \alpha=\mathrm{arctg}(1/\mu)=\mathrm{arcctg}{\mu}\), максимальна можлива швидкість спортсмена необмежено зростає. Отже, поперечного проковзування коліс не буде ні в за якому разі. При цьому, як видно з формули (3),
\( \vartheta=\mathrm{arcctg}\mu+\mathrm{arctg}\mu=\frac{\pi}{2}\),
тобто спортсмен з байком будуть розташовані в горизонтальній площині. В давнину це демонстрували в цирках шапіто в атракціоні під назвою "Перегони по вертикальній стіні".
| Задача 2.20 |
| Задача 2.20 |
Вага тіла на полюсі планети є на η = 5% більша, ніж на екваторі; тривалість доби T = 10 год.
Визначити
середню густину речовина планети ρ.
|
Дано: T = 10 год η = 5% |
|
ρ – ? |
Розв'язання
Насамперед згадаймо, що вага \( \vec{P}\) є силою тиску тіла на горизонтальну опору внаслідок гравітації. Відповідно, на саме тіло діють сили всесвітнього тяжіння \( \vec{F}\) та реакції опори \( \vec{N}\), рис. 2.20. При цьому за третім законом Ньютона P = N.

Розглянемо вказані сили в інерціальній системі відліку, пов'язаній з центром планети. На полюсі тіло перебуває в спокої, отже, \( \vec{F}\) + \( \vec{N}\) = 0, і вага тіла
|
Pп = F |
(1) |
На екваторі тіло через добове обертання планети рухається по колу і має доцентрове прискорення \( \vec{a}\). Тож
| \( {F}-{P}_{е}=m{a}\) \( \Rightarrow \) \({{P}_{\operatorname{e}}}=F-ma\), |
(2) |
тобто добове обертання планети є причиною зменшення ваги тіла на екваторі.
Позаяк за умовою Pп – Pe =ηPп, то з рівнянь (1) і (2) маємо:
ηF = ma,
де величини F і а визначаються формулами (2.6) і (1.28), відповідно. Отже,
\(\eta \frac{GM}{{{R}^{2}}}={{\omega }^{2}}R\).
Звідси, виразивши масу планети через густину ρ, як M=(4/3)πR3 ρ , та кутову швидкість через тривалість доби, як ω = 2π/Т , отримаємо відповідь:
\( \rho=\frac{3\pi}{\eta{GT^{2}}}\) ≈ 2,2·1о3 кг/м3.
Нагадування. При обчисленнях не забувайте всі величини виражати в основних одиницях.