ФІЗИКА ДЛЯ БАКАЛАВРІВ. КОЛИВАННЯ І ХВИЛІ
Частина І. КОЛИВАННЯ
6. Змінний струм
‹
Одним із важливих для практики видів вимушених електричних коливань є змінний струм. У широкому значенні змінним струмом називають будь-які періодичні вимушені коливання струму та напруги в електричному колі. Але зазвичай під змінним струмом розуміють синусоїдальний струм, який змінюється за гармонічним законом. Це пояснюється тим, що саме за таким законом змінюється з часом ЕРС потужних індукційних генераторів на електростанціях, які дають більшу частину всієї споживаної людством електричної енергії. Далі розглядаються такі питання:
6.1. Закон Ома для змінного струму
6.2. Резонанс у колі змінного струму
6.3. Потужність у колі змінного струму
6.1. Закон Ома для змінного струм
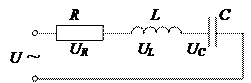 |
Найпростішим повним за складом колом змінного струму є послідовний контур, який включає резистор R, конденсатор C і котушку індуктивності L (див. схему), на які подається гармонічна напруга
|
u = U0cosωt. |
(6.1) |
Але на відміну від коливального контура, в загальному випадку наявність у колі всіх полічених елементів не є обов’язковою. Зокрема це стосується котушки індуктивності. Тому в теорії змінного струму вона розглядається не як джерело ЕРС самоіндукції, а як пасивний елемент кола, що разом з іншими живиться від генератора змінної напруги.
Раніше (ЕЛЕКТРИКА І МАГНЕТИЗМ, частина ІІІ) було показано, що змінні струми практично завжди є квазістаціонарними. Тому, відповідно до другого правила Кірхґофа, для миттєвих значень напруг на ділянках послідовного кола можна записати:
|
uR + uC + uL = U0cosωt. |
(6.2) |
При цьому струм у всіх ділянках кола в кожен момент часу однаковий, і виражається загальним рівнянням
|
|
(6.3) |
У випадку стаціонарного (постійного) струму зв’язок між струмом та напругою, що подається на послідовне коло, визначається законом Ома. Чи це так і для змінного струму, не є очевидним і потребує спеціального розгляду. Спочатку проаналізуємо зв’язок між струмом і напругою для кожної ділянки кола окремо.
Резистор у колі змінного струму. Активний опір. Резистор по суті – то є просто провідник із певним опором R , для якого в кожну мить виконується закон Ома u = iR . Отже, рівняння коливань напруги на опорі R, згідно з (6.3), має вигляд:
|
|
(6.4) |
Відмітимо, що струм і напруга на опорі R змінюються синфазно, і їхні амплітуди пов’язані співвідношенням:
|
|
(6.5) |
У колах змінного струму крім резисторів фігурують і котушки індуктивності та конденсатори, які теж чинять опір протіканню струму. Тому в теорії змінного струму опір R, що зумовлений розсіюванням носіїв струму і є причиною виділення у провіднику джоульового тепла, називають активним опором.
Котушка індуктивності та конденсатор у колі змінного струму. Реактивні опори. При протіканні змінного струму по котушці індуктивності напруга на ній визначається як:
\( {U}_{L}=L\frac{\mathrm{d}I}{\mathrm{d}t}\).
Тому, згідно з (6.3), напруга на котушці змінюється за законом:
|
|
(6.6) |
Отже,
коливання напруги на котушці за фазою випереджають коливання струму на π/2, або чверть періоду,
і їхні амплітуди пов’язані співвідношенням:
|
\( {U}_{L0}=I_{0}\omega{L}\) або \( {I}_{0}=\frac{U_{L0}}{X_{L}}\), |
(6.7) |
де уведено позначення
|
\( {X}_{L}=\omega{L} \). |
(6.8) |
Установимо тепер зв’язок між струмом i у колі та напругою uс на конденсаторі. При протіканні струму в колі з конденсатором заряд, який проходить по провідниках, потрапляє на обкладку конденсатора. Тому кожної миті сила струму в колі дорівнює швидкості зміни заряду конденсатора: і = dq/dt, тож
\( dq=idt\quad \Rightarrow \quad q=\int{idt}\).
Відповідно, напруга на конденсаторі uС = q/С визначається, як|
\( {{u}_{c}}={{U}_{C0}}\cos \left( \omega t-\varphi -\frac{\pi }{2} \right)\). |
(6.9) |
Таким чином,
коливання напруги на конденсаторі за фазою відстають від коливань струму на π/2, або чверть періоду.
При цьому їхні амплітуди пов’язані співвідношенням:
|
\( {U}_{C0}=I_{0}X_{C}\) або \( {I}_{0}=\frac{U_{C0}}{X_{C}} \), |
(6.10) |
де уведено позначення
|
\( {X}_{C}=\frac{1}{\omega{C}}\). |
(6.11) |
Порівняння виразів (6.7), (6.10) із (6.5) показує, що котушка індуктивності та конденсатор обмежують амплітуду струму при заданій амплітуді напруги, аналогічно до того, як це робить резистор. Тому можна говорити, що індуктивність і ємність теж створюють опір для протікання змінного електричного струму. Відповідно, величина XL, яка визначається формулою (6.8), називається реактивним індуктивним опором, а величина ХС (формула (6.11)) — реактивним ємнісним опором.
Отримані співвідношення (6.5), (6.7) і (6.10) показують, що на кожному опорі амплітуди струму та напруги пов’язані між собою законом Ома. Але для миттєвих значень він не виконується. Справді, з рівнянь (6.3), (6.6) і (6.9) випливає, що
|
|
(6.12) |
і
|
|
(6.12а) |
тобто
миттєва величина струму не є прямо пропорційною напрузі,
як того вимагає закон Ома. Відповідно, реактивний опір, на відміну від активного, не можна трактувати як коефіцієнт пропорційності між напругою та струмом на котушці або на конденсаторі.
Властивості реактивних опорів є доволі специфічними. З одного боку реактивний опір, подібно до активного, залежить від параметрів відповідного пристрою – котушки індуктивності чи конденсатора. Але на відміну від активного,
реактивні опори (6.8), (6.11) залежать від частоти струму.
Тому, якщо на коло подати постійну напругу (ω = 0), то реактивні опори ХL = 0 і XC → ∞. Це абсолютно природньо: адже для постійного струму котушка являє собою просто шматок дроту, а конденсатор – розрив кола. Якщо котушки в колі взагалі немає, то знову маємо L = 0, і ХL = 0. Зрозуміло, що за відсутності конденсатора так само ХС = 0, але з (6.11) при цьому випливає досить дивний формальний висновок: C → ∞. Цей “парадокс” має просте пояснення. Відсутність конденсатора означає відсутність у колі розриву провідності, отже, “викидаючи” з кола конденсатор, ми з’єднуємо провідники на місці його розташування. Тому формальний перехід до випадку “коло без конденсатора” можна здійснити, подумки наближаючи пластини конденсатора аж до дотику. При цьому відстань між пластинами конденсатора d = 0, і “все стає на місця”: ємність C = ∞, і опір XC = 0.
З ємнісним опором пов’язано ще одне питання. Опір ХС ми трактуємо як величину, що пов’язує амплітуди напруги та струму в конденсаторі, тоді як заряджені частинки-носії струму рухатися в діелектрику між пластинами конденсатора не можуть. І дійсно, стаціонарний струм може протікати тільки по замкнених провідниках. Але змінний струм можливий і при розриві провідності, як от у колі з конденсатором. При цьому із загальних рівнянь електродинаміки (ЕЛЕКТРИКА І МАГНЕТИЗМ, V, п. 2) випливає, що лінії струму провідності, які розриваються на пластинах конденсатора, замикаються всередині лініями струму зміщення, котрий є мірою швидкості зміни електричного поля всередині конденсатора. Отже
струм конденсатора – то є струм зміщення,
котрий в кожен момент часу збігається із струмом провідності в провідниках, які підходять до обкладок.
Імпеданс. Закон Ома для змінного струму. Встановимо тепер, як струм у колі пов’язаний з напругою на вході (напругою генератора). Вище вже говорилося, що в послідовному колі за умови квазістаціонарності напруга на вході дорівнює сумі напруг на всіх ділянках кола, а струм скрізь однаковий, так само, як у випадку стаціонарного (постійного) струму. Тому може здатися, що величина змінного струму, як і у випадку постійного, дорівнює відношенню напруги на вході до суми опорів усіх ділянок кола. Але насправді це не так, оскільки напруги на різних ділянках кола мають різні фази (див. рівняння (6.1),(6.4), (6.6) і (6.9)).
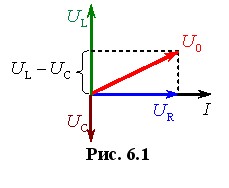
Для встановлення зв’язку між змінним струмом та напругою побудуємо векторну діаграму кола так, як це робилося при розгляді вимушених коливань у контурі (п. 5, рис. 5.1). При цьому врахуємо, що фаза напруги на індуктивному опорі випереджає, а на ємнісному – відстає від фази струму на π/2. З отриманої векторної діаграми, котра показана на рис. 6.1, випливає, що
|
\( {U}_{0}^{2}=U_{R}^{2}\left(U_{L}^{2}-U_{C}^{2}\right) \). |
(6.13) |
|
|
|
Відтак, урахувавши (6.5), (6.9) і (6.10), одержимо
|
\( {U}_{0}=I_{0}\sqrt{R^{2}+\left(X_{L}-X_{C}\right)^{2}}\). |
(6.14) |
Величина
|
X = XL - XC |
(6.15) |
називається реактивним опором, а величина
|
\( {Z}=\sqrt{R^{2}+X^{2}} \) |
(6.16) |
називається повним опором, або імпедансом послідовного кола змінного струму. Тож співвідношення (6.14) між амплітудами напруги та струму набуває вигляду:
|
\( {U}_{0}=I_{0}Z \), або \( {I}_{0}=\frac{U_{0}}{Z}\) |
(6.17) |
і є подібним до співвідношення між напругою та силою постійного струму. Тому воно називається законом Ома для змінного струму. З урахуванням (6.8), (6.11) і (6.15), імпеданс послідовного кола та закон Ома в розгорнутому вигляді записуються, як
|
\( {Z}=\sqrt{R^{2}+\left(\omega{L}-\frac{1}{\omega{C}}\right)^{2}} \), |
(6.18) |
|
|
\( {I}_{0}=\frac{U_{0}}{\sqrt{R^{2}+(\omega{L}-\frac{1}{\omega{C}}})^{2}}\). |
(6.19) |
Із векторної діаграми рис. 6.1 також випливає, що зсув фаз φ між струмом і напругою на вході кола визначається виразом:
|
|
(6.20) |
Стосовно закону Ома для змінного струму необхідно зробити наступні зауваження:
1. Поняття реактивних опорів й імпедансу та їхні вирази введені для гармонічних (синусоїдальних) струмів. Тому всі розглянуті співвідношення включно із законом Ома стосуються тільки таких струмів.
2. Закон Ома (6.17) виконується для амплітудних і не виконується для миттєвих значень струму та напруги. Це випливає з рівнянь (6.1), (6.3) і виразу (6.17):
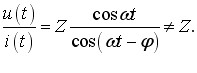
Така “невідповідність” пояснюється зсувом фаз φ між струмом і напругою, через що вони набувають своїх амплітудних значень у різні моменти часу. Тому кожної миті напруга і струм складають не однакові й не фіксовані частки від амплітудних значень. Через це за великим рахунком змінний струм не не задовольняє закон Ома, позаяк сила струму не є прямо пропорційною напрузі. Але для практики це нічого не вартує, бо, через швидку зміну, значущими є лишень усереднені характеристики змінного струму, що залежать тільки від амплітуд і тому підпорядковуються законові Ома.
6.2. Резонанс у колі змінного струму
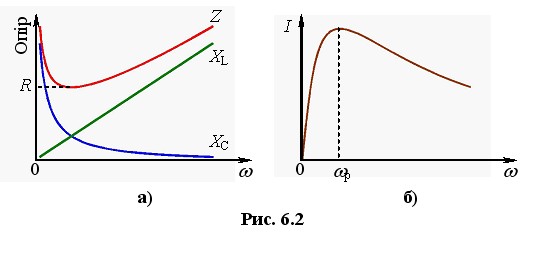
Реактивні опори (6.8), (6.11) та імпеданс (6.18) залежать від частоти, як показано на рис. 6.2а. При зростанні частоти індуктивний опір збільшується, а ємнісний зменшується. Тому, коли опори ХL і ХС зрівнюються, то реактивний опір ХL – ХС, = 0 й імпеданс, згідно з (6.18), має мінімальне можливе значення Z = R . Відповідно, амплітуда струму (6.19) набуває максимального можливого при заданій амплітуді напруги на вході значення
|
\( {I}_{p}=\frac{U_{0}}{R}\) |
(6.21) |
і надалі спадає (рис. 6.2б). Тобто, в колі змінного струму спостерігається резонанс. Резонансна частота ωp визначається умовою XL = XC, отже згідно з (6.8) і (6.11),
|
\( \omega_{p}L=\frac{1}{\omega_{p}C} \) \(\Rightarrow \) \( \omega_{p}=\frac{1}{\sqrt{LC}}=\omega_{0} \). |
(6.22) |
|
|
При резонансі напруга на активному опорі кола має найбільше можливе значення, рівне напрузі генератора, а сумарна напруга на реактивних опорах дрпівнює нулю. Але напруги окремо на котушці індуктивності UL = IpXL та на конденсаторі UC = IpXC не дорівнюють нулеві. Згідно з (6.8), (6.11), (6.21), і (6.22), вони визначаються, як
|
\( {U}_{L}=U_{C}=\frac{U_{0}}{R}\sqrt{\frac{L}{C}}\), |
(6.23) |
і можуть виявитися набагато вищими, ніж амплітуда напруги генератора. Це має враховуватися, бо при резонансі може виникнути загроза електричного пробою ізоляції провідників.
Як видно з (6.22), резонансна частота струму в колі збігається із власною частотою коливального контура (4.10), що має такі самі індуктивність і ємність. Всі інші розглянуті співвідношення для кола змінного струму теж збігаються з аналогічними співвідношеннями, що характеризують коливальний контур. У цьому не важко переконатися, зробивши у відповідних виразах для контура заміни:
\( {\omega_{0}}=\frac{1}{\sqrt{LC}}\), \( {\omega{L}}=X_{L} \) і \( \frac{1}{\omega{C}}=X_{C} \).
Указаний збіг є цілком природнім, адже коливальний контур принципово не відрізняється від повного кола змінного струму. Відміна полягає тільки у співвідношенні параметрів: активний опір R у реальних коливальних контурах є дуже малим, а в силових електричних колах змінного струму, напроти, великим.
6.3. Потужність у колі змінного струму
Можливості отримання корисної енергії в тому чи іншому електричному пристрої визначаються роботою та потужністю електричного струму в колах цього пристрою. Розглянемо, від чого залежить потужність на окремих ділянках та в усьому колі змінного струму.
Потужність на активному опорі. Діючі значення напруги та струму. Спочатку розглянемо потужність струму, що виділяється на резисторі. Миттєва потужність на будь-якій ділянці кола дорівнює добутку миттєвих значень струму та напруги. Відповідно, на резисторі вона, згідно з (6.3) і (6.4), визначається виразом:
|
\( {P}_{R}=iu_{R}=I_{0}U_{R0}\cos^{2}(\omega{t}-\varphi{)}\). |
(6.24) |
Але, позаяк змінні струми мають високу частоту, практично значимою є тільки середня потужність \( {P}=\langle{p}\rangle \), тобто величина
|
\( {P}_{R}=I_{0}U_{R0}\langle\cos^{2}(\omega{t}-\varphi{)}=\frac{I_{0}U_{R0}}{2}\langle{1}+\cos{(2}(\omega{t}-\varphi{)})\rangle \). |
(6.24а) |
Середнє значення функцій косинус і синус дорівнює нулеві, тому, з урахуванням (6.5),
|
\( {P}_{R}=\frac{I_{0}U_{R0}}{2}=\frac{I_{0}^{2}R}{2}=\frac{U_{0}^{2}}{2R}\). |
(6.25) |
Ці формули можна записати зручніше, увівши так звані “діючі” (або “ефективні”) значення струму та напруги, котрі виражаються через амплітуди як
|
\( {I}=\frac{I_{0}}{\sqrt{2}}\) і \( {U}=\frac{U_{0}}{\sqrt{2}}\). |
(6.26) |
Відтак формули (6.25) набувають вигляду:
|
\( {P}_{R}=IU_{R}=I^{2}R=\frac{U_{R}^{2}}{R}\), |
(6.27) |
і стають такими самими, як і для постійного струму. Отже, можна сказати, що
діючі значення напруги та сили змінного струму – це такі величини напруги та сили постійного струму, при яких у провіднику виділяється така сама потужність, як і при заданому змінному струмі.
Іншими словами, діючі значення дорівнюють характеристикам постійного струму, котрий є енергетично еквівалентним даному змінному струмові.
Із означень (6.26) випливає, що всі співвідношення, в які входять амплітуди струму й напруги, зберігаються і для діючих значень. Зокрема, це стосується співвідношень, які виражають закон Ома для всього кола (6.17) та окремих ділянок (6.5), (6.7), (6.10):
|
U = IZ, UR =IR, UL = IXL, UC = IXC. |
(6.28) |
Діючі значення є дуже зручними і тому загально прийнятими на практиці. Зокрема, всі вимірювальні прилади змінного струму проградуйовані в діючих значеннях. Тому в техніці та побуті, коли мова йде про величину змінного струму чи напруги, терміни “діючі значення” спеціально не вживають, і слова “напруга в мережі дорівнює 220 В” або напис на вилці чи розетці “220 В, 6 А” по замовчуванню означають саме діючі значення. Що ж до амплітуди напруги в освітлювальній мережі, то вона складає \( {U}_{0}=220\cdot\sqrt{2}\approx{311}\) В. Ще одне зауваження про терміни. Діючі значення були уведені через потужність змінного струму, що виділяється на резисторі R. На відміну від котушки індуктивності та конденсатора, ця потужність виділяється при будь-якому напрямку і фазі φ струму. Можна сказати, що резистор "активно" споживає енергію джерела струму, тому опір R називають активним опором. Слід також зауважити, що активний опір в колі змінного струму не є тотожнім до опору в колі постійного струму. Ці величини збігаються тільки в нерухомих колах, де опір R зумовлюється виключно розсіюванням ("гальмуванням") носіїв струму при зіткненнях із іншими частинками провідника і є фактором необоротного перетворення енергії електричного струму на тепло. Але, до прикладу, в електричних двигунах споживана енергія струму переходить не тільки в тепло, а й, головно, в механічну роботу. Тому активний опір працюючого двигуна є набагато більшим, ніж нерухомого.
Потужність на котушці індуктивності та на конденсаторі. Суттєва відмінність між реактивними опорами XL і XC та активним опором R виявляється в процесах перетворення енергії в колі змінного струму. Аби в цьому переконатися, знайдемо миттєву та середню потужності струму на індуктивності та на ємності. Вказані миттєві потужності визначаються добутком миттєвих значень струму (6.3) та відповідної миттєвої напруги (6.6) і (6.9):
|
pL = –\(\frac{1}{2}{{I}_{0}}{{U}_{L0}}\sin \left( 2\omega t-2\varphi \right)\) = –\(I{{U}_{L}}\sin \left( 2\omega t-2\varphi \right)\)
|
(6.29) |
|
|
pC = \(\frac{1}{2}{{I}_{0}}{{U}_{C0}}\sin \left( 2\omega t-2\varphi \right)\) =\(I{{U}_{C}}\sin \left( 2\omega t-2\varphi \right)\). |
(6.29а) |
І, позаяк середня величина \( \langle\sin{(}2\omega{t}-2\varphi{)}\rangle={0}\), середні потужності на котушці та на конденсаторі
|
PL = PC = 0. |
(6.30) |
Цей, можливо, неочікуваний результат має просте пояснення. Ані в котушці індуктивності, ані в конденсаторі не відбувається ніяких перетворень електричної енергії в інші форми, наприклад у тепло. Через це магнітна енергія, яка накопичується в котушці під час збільшення струму від нуля до амплітудного значення, при подальшому зменшенні струму до нуля повністю повертається до генератора чи інших частин кола. Подібні процеси відбуваються й при збільшенні та зменшенні напруги на конденсаторі. Тому, на відміну від активного опору, стосовно індуктивності та ємності слід говорити не про споживання енергії від генератора, а тільки про енергообмін між ними та генератором. Саме з цієї причини котушку індуктивності та конденсатор називають реактивними елементами кола, а величини XL і XC – реактивними опорами.
Повна потужність у колі змінного струму. Згідно з (6.1) і (6.3), миттєва потужність струму у всьому колі
\( {p}=iu=I_{0}U_{0}\cos{(}\omega{t}-\varphi{)}\cos\omega{t}\).
За допомогою відомої формули тригонометрії цей вираз можна записати, як
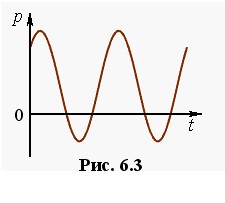
|
|
(6.31) |
|
|
|
Звідси видно, що миттєва потужність, яка виділяється в колі, коливається навколо рівня 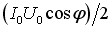 з подвоєною частотою струму. Можливий вигляд графіка p(t), згідно з (6.31), показаний на рис. 6.3. Наявність на графіку ділянок із p < 0 може видатися несподіваною, але легко пояснюється присутністю в колі реактивних опорів. Раніше вже говорилося про те, що, на відміну від резистора, котушка індуктивності та конденсатор не перетворюють енергію струму на інші форми, а лише періодично накопичують, а потім повністю повертають її в коло (див. (6.29), (6.29а)). Причому ці процеси відбувається не синхронно. Тому може статися, що протягом певних частин періоду енергія, яку віддають реактивні елементи перевищує ту, що поглинається на активному опорі. В такому разі “зайву” енергію коло віддає в генератор, а формальною мовою це означає, що воно споживає від’ємну потужність.
з подвоєною частотою струму. Можливий вигляд графіка p(t), згідно з (6.31), показаний на рис. 6.3. Наявність на графіку ділянок із p < 0 може видатися несподіваною, але легко пояснюється присутністю в колі реактивних опорів. Раніше вже говорилося про те, що, на відміну від резистора, котушка індуктивності та конденсатор не перетворюють енергію струму на інші форми, а лише періодично накопичують, а потім повністю повертають її в коло (див. (6.29), (6.29а)). Причому ці процеси відбувається не синхронно. Тому може статися, що протягом певних частин періоду енергія, яку віддають реактивні елементи перевищує ту, що поглинається на активному опорі. В такому разі “зайву” енергію коло віддає в генератор, а формальною мовою це означає, що воно споживає від’ємну потужність.
Розглянутий аналіз процесів перетворення енергії в колі є важливими для теорії, але практичне значення має лише середня потужність струму \( {P}=\langle{p}\rangle \), яку споживає коло. Тому на практиці під потужністю змінного струмурозуміють саме середнє значення величини (6.31):
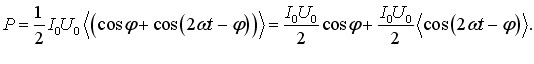
Урахувавши, що 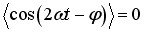 , і перейшовши від амплітуд до діючих значень, отримуємо:
, і перейшовши від амплітуд до діючих значень, отримуємо:
|
|
(6.32) |
Отже, потужність, яка виділяється в колі змінного струму, залежить не тільки від сили струму та напруги, а й від зсуву фаз між ними. Відповідно, величина cosφ називається коефіцієнтом потужності (в інженерній практиці — “косинусом фі”. Його вираз можна знайти безпосередньо з векторної діаграми (рис. 6.1) як UR/U0, або через формулу (6.20):
|
|
(6.33) |
Коефіцієнт потужності відіграє важливу роль в електротехніці, оскільки визначає ефективність використання електричної енергії. Справді, якщо cosφ << 1, то навіть при великому струмі та напрузі коло майже не споживає енергії з мережі живлення. При цьому генератор працює вхолосту, і необхідні для генерації струму енергетичні ресурси витрачаються марно. Тому коефіцієнт потужності завжди необхідно максимально підвищувати. Для цього треба наближати імпеданс до активного опору, тобто зменшувати реактивну складову імпедансу. З цією метою в коло з великою індуктивністю, яку мають, скажімо, обмотки електричного двигуна, включають компенсуючі конденсатори. Аналогічно в коло з великою ємністю включають додаткові котушки індуктивності. Таким чином, хоча середня потужність на реактивних опорах дорівнює нулеві, ці опори відіграють суттєву роль в енергетиці кола змінного струму. Тому в електротехніці крім потужності (6.32), яку називають активною потужністю, розглядають так звану реактивну потужність Q, яку вимірюють не у ватах, а у “варах” (скорочення від "вольт-ампер реактивний") і визначають за формулою Q = IUsinφ. Але детально це питання розглядають не в загальній фізиці, а в електротехніці.
Контрольні запитання
1. Що таке ємнісний опір? Якою формулою він визначається?
2. Що таке індуктивний опір? Якою формулою він визначається?
3. Якою формулою визначається повний реактивний опір кола?
4. Якою формулою визначається імпеданс (повний опір) послідовного кола?
5. Якою формулою визначається імпеданс (повний опір) послідовного кола, в якому немає конденсатора?
6. Якою формулою визначається імпеданс (повний опір) послідовного кола, в якому немає котушки індуктивності?
7. Якою формулою визначається імпеданс (повний опір) ідеального коливального контура?
8. Сформулюйте та запишіть закон Ома для змінного струму.
9. Чи справджується закон Ома для миттєвих значень змінного струму та напруги? Дайте обґрунтовану відповідь.
10. В якому випадку коливання струму в послідовному колі за фазою випереджають коливання напруги генератора?
11. В якому випадку коливання струму в послідовному колі за фазою відстають від коливань напруги генератора?
12. В якому випадку коливання струму в послідовному колі відбуваються в одній фазі з коливаннями напруги генератора?
13. Чи можуть коливання струму за фазою випереджати коливання напруги генератора в колі без конденсатора?
14. Чи можуть коливання струму за фазою відставати від коливань напруги генератора в колі без котушки індуктивності?
15. При якій частоті амплітуда струму в послідовному колі з параметрами R,L,C буде максимальною?
16. Від чого та як залежить максимальна можлива амплітуда змінного струму в колі?
17. Отримайте вирази (6.23).
18. Якими формулами визначаються діючі значення змінного струму та напруги та який фізичний зміст вони мають?
19. Чому дорівнює середня потужність змінного струму, що виділяється на активному опорі? Ємнісному опорі? Індуктивному опорі?
20. Якими формулами визначається повна потужність у колі змінного струму?
21. Чи може в колі змінного струму бути від’ємною: а) миттєва потужність струму; б) середня потужність струму?
22. Що таке коефіцієнт потужності та як його можна змінювати для підвищення потужності, що виділяється в колі змінного струму?
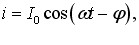
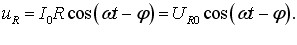
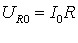 або
або 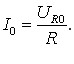
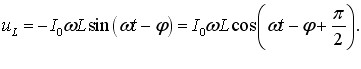
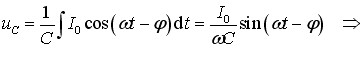
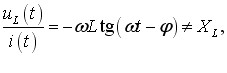
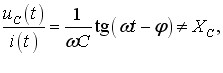
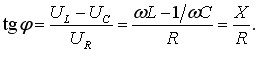
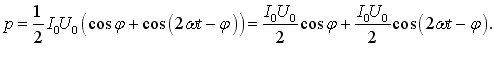
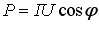 .
.