ФІЗИКА ДЛЯ БАКАЛАВРІВ. МОЛЕКУЛЯРНА ФІЗИКА ТА ТЕРМОДИНАМІКА
VI. ЯВИЩА ПЕРЕНОСУ
Розглянуті в попередніх лекціях відомості стосуються рівноважних станів і процесів, але за відповідних умов їх можна використовувати й для нерівноважних систем. В різних частинах нерівноважної замкненої системи певні параметри стану (температура, тиск, тощо) та інші характеристики системи ( приміром, концентрація молекул даного сорту в суміші) мають не однакові значення. У процесі встановлення термодинамічної рівноваги відбувається вирівнювання подібних неоднорідностей, яке супроводжується виникненням потоків відповідних фізичних характеристик системи. Скажімо, якщо в одній частині системи температура вища, ніж в іншій, то від більш нагрітої частини до менш нагрітої буде переноситися теплова енергія, при вирівнюванні концентрації частинок від області з більшою їхньою концентрацією до області з меншою буде переноситися маса, тощо. Тому подібні явища називаються явищами переносу.
Явища переносу спостерігаються і в незамкнених системах. При цьому, якщо неоднорідність розподілу характеристик системи штучно підтримувати на незмінному рівні, перенесення відповідних величин буде стаціонарним, тобто, їхні значення не залежитимуть від часу, так само, як у рівноважній системі. Тому для стаціонарних явищ переносу є чинними закони молекулярно-кінетичної теорії та термодинаміки.
Нижче розглянуті наступні питання:
1. Емпіричні закони явищ переносу
2. Середня довжина вільного пробігу молекул
3. Молекулярно-кінетична теорія явищ переносу в газах
1. Емпіричні закони явищ переносу
|
\(\Phi=\frac{\Delta{A}}{\Delta{t}}\), |
(6.1) |
де ΔA – кількість величини А, що переноситься крізь цю поверхню за час Δt.
У загальному випадку потік Ф може бути неоднорідним, коли в різних точках інтенсивність перенесення є не однаковою. Тому для опису перенесення величини А в кожній точці простору вводять густину потоку
|
\({j}=\frac{\Delta\Phi}{\Delta{{S}_{\bot }}}\), |
(6.1а) |
де ΔΦ – потік крізь елементарну площинку \(\Delta{{S}_{\bot }}\), перпендикулярну до напрямку переносу.
Перенесення величини А вздовж певного напряму завжди є зумовлене неоднорідним розподілом у цьому напрямі якоїсь іншої величини В. Наприклад, перенесення теплоти Q від батареї опалення до якоїсь віддаленої точки в кімнаті зумовлене наявністю перепаду температури Т між батареєю та цією точкою. Мірою неоднорідності величини В у заданому напрямку ОХ є її градієнт, тобто швидкість зміни dB/dх у цьому напрямі.
Розглянуті поняття й величини дозволяють аналітично виразити емпіричні (встановлені на досліді) закони стаціонарних явищ переносу, що розглядаються далі.
Теплопровідність. Уявімо дві паралельні плоскі пластини, розміщені в однорідному теплопровідному середовищі, котрі підтримуються при сталих температурах T1 і T2 (T1 > T2). За таких умов між пластинами у показаному на рис. 6.1 напрямі ОХ встановлюється стаціонарне перенесення тепла[1].
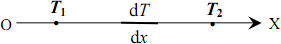
|
\({{j}_{Q}}=-\varkappa \frac{\text{d}T}{\text{d}x}\), |
(6.2) |
де коефіцієнт пропорційності \(\kappa \) коефіцієнтом теплопровідності
Відповідно, кількість теплоти, що переноситься через ділянку перерізу потоку площею ΔS за проміжок часу Δt дорівнює :
|
\(\Delta Q=-\varkappa \frac{\text{d}T}{\text{d}x}\Delta S\Delta t\). |
(6.3) |
(Примітка. Знак “–” у виразах (6.2) і (6.3) є зумовлений тим, що перенесення будь-якої величини (тут Q) завжди відбувається у напрямку менших значень тієї величини (тут T), градієнт якої є причиною переносу. Тож у напрямку перенесення тепла Q > 0, тоді як
Дифузія. Так називається взаємопроникнення різних речовин у сумішах, якщо концентрації частинок у них нерівномірно розподілені по об’єму. До прикладу, проявом дифузії є поширення запаху парфумів у повітрі, або розширення області забарвлення при вміщенні у воду чи на фільтрувальний папір краплі рідкого барвника. Дифузія спостерігається й у хімічно однорідній речовині (газі), якщо концентрація частинок різна в різних місцях. У такому випадку говорять про самодифузію.
Імовірність теплового руху окремої частинки за всіма напрямками однакова, тому будь-якої миті кількість частинок, які рухаються в бік меншої концентрації, більша, ніж кількість частинок, які рухаються в зустрічному напрямку. Через це виникає потік частинок у напрямку зони меншої концентрації. Якщо в газі підтримується сталий градієнт концентрації частинок у напрямку певної осі ОХ, то, як свідчить дослід, сумарна кількість частинок, які проходять за час Δt крізь площинку ΔS, перпендикулярну до напрямку потоку, дорівнює
|
\({N}=-D\frac{\mathrm{d}n}{\mathrm{d}x}\Delta{S}\Delta{t}\), |
(6.4) |
де dn/dx – градієнт концентрації, і D – величина, що залежить від індивідуальних властивостей частинок речовини і називається коефіцієнтом дифузії. Відповідно, густина потоку частинок \({j_n}=N/(\Delta{S}\Delta{t}) \) визначається рівнянням
|
\({j_n}=-D\frac{\mathrm{d}n}{\mathrm{d}x}\), |
(6.5) |
яке називається рівнянням дифузії, або рівнянням Фіка.
Якщо обидві частини рівняння (6.5) помножити на масу однієї молекули m0 і врахувати, що nm0 = ρ – густина речовини, то в правій частині отримаємо градієнт густини dρ/dx, а в лівій – густину потоку маси \({j_m}=m/(\Delta{S}\cdot\Delta{t})\), де \({m=m_0 N}\) – маса речовини, що переноситься. Відтак рівняння (6.5) трансформується в рівняння густини масового потоку:
|
\({j_m}=-D\frac{\mathrm{d}\rho}{\mathrm{d}x}\). |
(6.5а) |
Внутрішнє тертя (в’язкість). До класичних явищ переносу відноситься також внутрішнє тертя, яке спостерігається в рухомій рідині або газі, коли сусідні шари речовини мають різні швидкості течії u1 і u2, як показано на рис. 6.2.
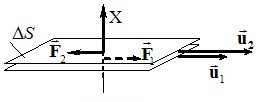
В цьому випадку частинки речовини за рахунок теплового хаотичного руху переходять з одного шару в інший, переносячи із собою відповідний імпульс упорядкованого руху. Унаслідок такого обміну повільний шар буде поповнюватися молекулами, що рухаються у напрямку течії з більшою швидкістю u2, а швидкий – молекулами, що мають меншу швидкість u1. Тому повільний шар буде прискорюватись, а швидкий – сповільнюватись. Це означає, що між шарами є певні сили взаємодії \(\vec{F}_1 \) і \(\vec{F}_2\), які називаються силами внутрішнього тертя. На досліді встановлено, що величина сили внутрішнього тертя залежить від індивідуальних властивостей речовини, площі взаємодіючих шарів ΔS та градієнту їхньої швикості й визначається, як
|
\({F}=\eta\left|\frac{\mathrm{d}u}{\mathrm{d}x}\right|\Delta{S}\). |
(6.6) |
Поділивши цей вираз на ΔS, отримаємо рівняння Ньютона, яке визначає силу внутрішнього тертя між шарами одиничної площі:
|
\({f}=\eta\left|\frac{\mathrm{d}u}{\mathrm{d}x}\right| \). |
(6.6а) |
Похідна під знаком модуля є градієнтом швидкості, який показує, як стрімко змінюється швидкість руху шарів рідини чи газу при переході від одного до іншого шару. Величина η називається коефіцієнтом внутрішнього тертя або динамічною в’язкістю речовини. Крім динамічної, розглядають і так звану кінематичну в’язкість
|
\(\nu=\frac{\eta}{\rho}\), |
(6.7) |
де ρ - густина речовини.
Сила внутрішнього тертя \(\vec{f}\) виникає внаслідок перенесення імпульсу від швидких шарів рідини чи газу до повільних. За другим законом Ньютона \({f}=\left|\mathrm{d}\vec{p}/\mathrm{d}t\right| \), причому в даному випадку права частина – то є імпульс, який переноситься за одиницю часу через одиничну площинку, тобто, густина потоку імпульсу \({j_p}\). Тому, з урахуванням напрямку переносу, рівняння (6.6) можна, подібно до (6.2) – (6.5а), подати як рівняння переносу імпульсу:
|
\({j_p}=-\eta\frac{\mathrm{d}u}{\mathrm{d}x}\). |
(6.8) |
2. Середня довжина вільного пробігу молекул
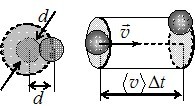
За таких умов середня кількість зіткнень < z′ > на довжині Δl (тобто, за час Δt) дорівнює кількості молекул у вказаному циліндрі: <z′ > = nπd2Δl, де п – концентрація молекул, \(\sigma=\pi{d^2}\) – так званий ефективний переріз молекули[2]. В дійсності рухається не одна, а всі молекули, тому ймовірність зіткнення даної молекули з якоюсь іншою визначається їхньою середньою відносною швидкістю, яка є в \(\sqrt{2}\) разів більша за середню арифметичну швидкість \(\langle{v}\rangle\).[3] Тому коректнішою оцінкою кількості зіткнень є величина
|
\({z}=\sqrt{2}n\pi{d^2}\Delta{l}=\sqrt{2}n\sigma\Delta{l}\). |
(6.9) |
Якщо на відстані \(\Delta{l}\) відбувається z зіткнень даної молекули з іншим, то середня довжина вільного пробігу \(\lambda=\Delta{l}/z \) і, згідно з (6.9),
|
\(\lambda=\frac{1}{\sqrt{2}\pi\sigma{n}}=\frac{1}{\sqrt{2}\pi{d^2{n}}}\). |
(6.10) |
Концентрація молекул пов’язана з тиском газу співвідношенням P = nkT. Тому середня довжина вільного пробігу молекул обернено пропорційна тиску газу, тож
|
\(\lambda_1 P_1=\lambda_2 P_2 \). |
(6.11) |
Середню довжину вільного пробігу молекул у газах можна визначати експериментально на основі явищ переносу. Тому з виразу (6.10) можна знайти ефективний переріз і ефективний діаметр молекули. Щодо точності таких вимірів слід зауважити наступне. По-перше, при підрахунку кількості зіткнень z (6.9) вважалося, що рухома молекула стикається з іншими молекулами в об’ємі прямого циліндра довжини Δl, тобто, що вона при зіткненнях не змінює напрямку руху. Насправді це не так. Тому указаний циліндр є ламаним і має дещо більший об’єм за рахунок “колін”. По-друге, молекули розглядались як кулі, хоча в дійсності довільна молекула складається з декількох атомів і не має симетрії кулі. Тому вираз (6.10) слід розглядати як оціночний. Але, попри це, уявлення про ефективний переріз та ефективний діаметр молекули виявляється досить плідним і загально вживаним.
Наостанок зауважимо, що із середньою довжиною вільного пробігу молекул пов’язане поняття вакуумного стану газу або технічного вакууму. При відкачуванні закритої посудини з газом середня довжина вільного пробігу в міру зниження тиску зростає й при певному тиску P0 стає рівною чи більшою за лінійні розміри посудини. Такий стан газу називається ультрарозрідженим або вакуумним. У вакуумному стані молекули газу практично не стикаються між собою, а тільки зі стінками посудини. Тому властивості ультрарозрідженого газу істотно відрізняються від його властивостей за звичайних умов. Наприклад, при високому вакуумі в газі практично відсутнє внутрішнє тертя та теплопровідність. Останнє використовують у посудинах Дьюара – посудинах із подвійними стінками, простір між якими відкачано до високого вакууму. Такі посудини забезпечують добру теплову ізоляцію від зовнішнього середовища. Прикладом використання посудин Дьюара в побуті є добре відомий кожному термос. В науці та техніці високоякісні посудини Дюара використовують, зокрема, для зберігання скраплених неорганічних газів (азот, кисень, водень, гелій), які мають дуже низькі (кріогенні) температури.
3. Молекулярно-кінетична теорія явищ переносу в газах
Розглянуті явища переносу спостерігаються в будь-яких речовинах мають спільні механізми і, як наслідок, виражаються схожими співвідношеннями (6.2) – (6.8). Але побудувати їхню кількісну теорію на основі молекулярно-кінетичних уявлень можна лише для газів, у яких практично відсутні сили зчеплення між молекулами.Дифузія. Нехай у газі підтримується незалежний від часу нерівномірний розподіл концентрації молекул у напрямку осі ОХ, як показано на рис. 6.4.
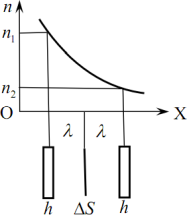
За таких умов у напрямі осі ОХ створюється стаціонарний потік молекул. Визначимо густину цього потоку в довільній точці х. Для цього виділимо в газі два тонкі шари 1 і 2 на відстані вільного пробігу молекул λ від точки х, для кожного з яких площа складає ΔS і товщина h << λ. В такому разі можна вважати, що крізь площинку ΔS проходять усі молекули кожного шару, котрі вилітають в її напрямку паралельно до осі ОХ. Також, ураховуючи рівноймовірність усіх напрямків теплового руху молекул, будемо вважати, що в кожному з двох можливих напрямів кожної з трьох координатних осей рухається (1/6) частина всіх молекул газу. Для виділених шарів це складає, відповідно, \({N_1}=(1/6)n_1\Delta{S}h\) і \({N_2}=(1/6)n_2\Delta{S}h\). Проліт усіх цих молекул крізь площинку ΔS триває протягом часу Δt = h/<v>, який потрібен, аби найвіддаленіші з них подолали відстань h між стінками шару при середній швидкості руху \(\langle{v}\rangle\). Відтак для густини потоку молекул отримуємо:
|
\({j}=\frac{1}{6}n\langle{v}\rangle \) |
(6.12) |
Відтак, згідно з означеннями (6.1а) і (6.1а) , густина зустрічних потоків молекул крізь площинку ΔS виражається, відповідно, як \({j_1}=(1/6)n_1\langle{v}\rangle \) і \({j_2}=(1/6)n_2\langle{v}\rangle \), а результуюча густина потоку дифузії
\({j_n}=\frac{1}{6}(n_1-n_2)\langle{v}\rangle \) = \(-\frac{1}{6}\Delta n\left\langle v \right\rangle \),
де Δn = n2 – n1 — приріст концентрації молекул уздовж осі ОХ на відстані Δx = 2λ.
Позаяк величина λ є дуже малою, то за канонами математичного аналізу можна записати \(\Delta{n}=(\mathrm{d}n/\mathrm{d}x)Δx=2\lambda (\mathrm{d}n/\mathrm{d}x) \)[4].
Відтак для густини потоку частинок при самодифузії остаточно отримаємо:
|
\({j_n}=-\frac{1}{3}\lambda\langle{v}\rangle\frac{\mathrm{d}n}{\mathrm{d}x}\), |
(6.13) |
де (dn/dx) — градієнт концентрації молекул, а множник
|
\({D}=\frac{1}{3}\lambda\langle{v}\rangle \) |
(6.13а) |
— коефіцієнт дифузії.
Таким чином, рівняння (6.13) повністю узгоджується з емпіричним рівнянням (6.5) та теоретично визначає коефіцієнта дифузії D ідеального газу.
Теплопровідність. Як говорилося в п.1, в середовищі між двома паралельними площинами, що підтримуються при сталих температурах T1 і T2, встановлюється певний не залежний від часу розподіл температур уздовж перпендикулярної до площин осі ОХ (рис. 6.5) та стаціонарний тепловий потік, зумовлений теплопровідністю, тобто не пов’язаний з рухом речовини (конвекцією).
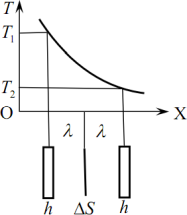
Теоретично закономірності цього процесу в ідеальному газі легко встановити за тією самою формальною схемою, що й у випадку дифузії, врахувавши, що при теплопровідності перенесення тепла спричинюється градієнтом температури, а не концентрації молекул. Тож знову виділимо в газі обабіч площинки ΔS на відстанях вільного пробігу молекул λ два шари 1 і 2 з такою самою площею і товщиною h << λ. Тоді можна вважати, що крізь площинку ΔS проходять усі молекули з кожного шару, котрі рухаються в її напрямі паралельно до осі ОХ. При цьому молекули з шару 1 є більш “гарячими”, ніж із шару 2, тож переносять із собою більшу кінетичну енергію E тепловового руху. Тому зустрічний рух обох пучків молекул супроводжується перенесенням тепловї енергії від гарячих до холодних зон, яку легко розрахувати.
Очевидно, що густина потоку енергії крізь площинку ΔS, що створюється кожним пучком молекул, дорівнює j = jмE, де jм – густина потоку молекул, і E – середня енергія теплового руху однієї молекули в пучку. Тож густина теплового потоку jq = j1 – j2, що створюється крізь площинку ΔS при зустрічному русі обох пучків, дорівнює
jq = jм(E1 – E2)
Енергія полекули визначається її кількістю ступенів свободи і та температурою газу за формулою (4.4): Е = (і/2)kT. Отже,
E1 – E2 = \(\frac{ik}{2}\left( {{T}_{1}}-{{T}_{2}} \right)=-\frac{ik}{2}\Delta T\)
Відтак, урахувавши, що при малій відстані між шарами Δx = 2λ зміна температури \(\Delta{T}=(\mathrm{d}T/\mathrm{d}x)Δx=2\lambda (\mathrm{d}T/\mathrm{d}x) \)[4], а густина потоку молекул виражається формулою (6.12), отримуємо наступний вираз густини теплового потоку при теплопровідності:
\({j_q}=-\frac{1}{3}\lambda\langle{v}\rangle\frac{ikn}{2}\cdot\frac{\mathrm{d}T}{\mathrm{d}x}\).
Множник ikn/2 можна подати зручніше, домноживши чисельник і знаменник на сталу Авогадро NA та масу молекули m0. Тоді, враховуючи, що m0n = ρ – густина, m0NА = М– молярна маса газу, а також формули (2.5), (5.2) і (5.6), отримаємо:
|
\({j_q}=-\frac{1}{3}\lambda\langle{v}\rangle\rho{c_V}\cdot\frac{\mathrm{d}T}{\mathrm{d}x}\). |
(6.14) |
Це і є теоретичне рівняння теплопровідності, причому коефіцієнт теплопровідності визначається виразом
|
\(\kappa=\frac{1}{3}\lambda\langle{v}\rangle\rho{c_V}\), |
(6.15) |
де ρ - густина газу, \({c_V}\) - питома теплоємність при сталому об’ємі.
Внутрішнє тертя (в’язкість). Як відмічалося раніше, внутрішнє тертя між шарами газу є зумовлене переносом імпульсу впорядкованого руху від шару до шару в напрямку зменшення швидкості (від’ємний напрям осі Х на рис. 6.2, що безпосередньо відображено в рівнянні (6.8). Молекулярний механізм в’язкості є повністю аналогічним до щойно розглянутого механізму теплопровідності. Тому для отримання теоретичного рівняння внутрішнього тертя в газі, не повторюючи всіх попередніх міркувань, достатньо заміни у виразах густини потоків енергію Е на імпульс упорядкованого руху молекули p = m0u. Тоді густина потоку імпульсу крізь площинку ΔS дорівнює:
\({j_p}=\frac{1}{6}n\langle{v}\rangle{m_0}(u_1-u_2)=-\frac{1}{6}n\langle{v}\rangle{m_0}\Delta{u}\) \(\Rightarrow \) \({j_p}=-\frac{1}{3}\lambda\langle{v}\rangle{nm_0}\frac{\mathrm{d}u}{\mathrm{d}x}\).
Урахувавши, що m0n = ρ – густина газу, отримаємо теоретичне рівняння густини потоку імпульсу:
|
\({j_p}=-\frac{1}{3}\lambda\langle{v}\rangle\rho\frac{\mathrm{d}u}{\mathrm{d}x}\), |
(6.16) |
а відтак і рівняння Ньютона (6.6 а), з таким виразом коефіцієнта внутрішнього тертя:
|
\(\eta=\frac{1}{3}\lambda\langle{v}\rangle\rho \). |
(6.17) |
Із виразів (6.13). (6.15) і (6.17) випливає, що, визначаючи коефіцієнти переносу дослідним шляхом, можна знайти середню довжину пробігу молекул, і, згідно з (6.10), ефективний переріз та діаметр молекули – параметри, які відіграють важливу роль у багатьох задачах молекулярної фізики. Тому цікаво проаналізувати, наскільки розглянута елементарна теорія узгоджується з експериментом.
Порівняння теоретичних та емпіричних рівнянь переносу показує, що теорія правильно відображає лінійний характер залежності густини потоку величини, які переноситься, від градієнту відповідного термодинамічного параметра газу. Розглянута теорія також адекватно показує, від яких величин залежать коефіцієнти переносу D, η і κ. Зокрема те, що всі коефіцієнти переносу повинні зростати при підвищенні температури, оскільки \(\langle{v}\rangle\sim\sqrt{T}\). Інший теоретичний прогноз полягає в тому, що коефіцієнти теплопровідності (6.15) та внутрішнього тертя (6.17) газів не залежать від тиску, оскільки густина ρ = nm0 є прямо пропорційною, а довжина вільного пробігу молекул λ– обернено пропорційною до концентрації молекул, а отже, й тиску газу. Дослід це підтверджує, що може здатися дивним, – адже зменшуючи концентрацію молекул, ми зменшуємо кількість “переносників” енергії у випадку теплопровідності та імпульсу у випадку внутрішнього тертя. Це справді так, але при тому, такою ж мірою збільшується довжини вільного пробігу молекул, тож і різниця значень величини, що переноситься кожною парою зустрічних молекул, а отже й густина потоку. Водночас, дійсна величина числових множників у коефіцієнтах переносу D, η і κ дещо відрізняється від 1/3 і є не однаковою для різних явищ переносу. Це пояснюється тим, що при виведенні розглянутих рівнянь відповідні процеси в газі розглядалися доволі спрощено.
2. За яких умов до явищ переносу можна застосовувати положення молекулярної фізики рівноважних процесів?
3. Що таке потік даної фізичної величина та густина потоку? Який зв’язок існує між ними?
4. Чи супроводжується тепловий потік переміщенням шарів газу від більш нагрітої області до менш нагрітої?
5. При прокачуванні рідини по трубі швидкість її руху є найбільшою на осі труби й найменша біля стінки. Який напрям має градієнт швидкості зумовлений цим потік імпульсу?
6. Що таке вакуумний стан газу? Якими мають бути розміри посудини, щоб газ у ній перебував у вакуумному стані?
7. Який “принцип дії” термоса? Оцініть, при якому максимальному тиску термос із відстанню між стінками 5 мм ще буде виконувати свою функцію – забезпечувати теплову ізоляцію вмісту від довкілля.
-------------------------
[1] Самі пластини не показані й розташовані перпендикулярно до площини рисунка.
[2] Як видно, ефективний переріз молекули дорівнює площі круга, в який має потрапити центр іншої молекули, щоби вони зіткнулися, тобто, достатньо сильно змінили свої швидкості внаслідок взаємодії. Діаметр та ефективний переріз молекули є певною мірою умовними величинами, зокрема, вони залежать від температури.
[4] Це випливає з того, що при малій зміні аргумента похідну можна наближено розглядати як відношення приросту функції до приросту аргумента: (dn/dx) ≈ (Δn/Δx)