ФІЗИКА ДЛЯ БАКАЛАВРІВ. МЕХАНІКА
V. ДИНАМІКА ТВЕРДОГО ТІЛА
1. Момент імпульсу
Імпульс частинки \(\vec{p}=m\vec{v}\) не містить інформації про просторову орієнтацію її траєкторії, що може бути важливим при розгляді руху сукупності тіл, до прикладу, планет у Сонячній системі. Недостатність імпульсу як міри руху виявляється й при розгляді обертання твердого тіла, бо, приміром, якщо вісь проходить через центр мас, імпульс тіла дорівнює нулю, хоча воно перебуває в русі. Тому, крім імпульсу, для характеристики руху в динаміці використовують величину, що називається моментом імпульсу.
1.2. Загальні рівняння динаміки системи
1.3. Закон збереження моменту імпульсу
Момент імпульсу. Нехай рухома частинка маси m має швидкість \(\vec{v}\) та імпульс \(\vec{p}=m\vec{v}\), а її положення відносно обраного початку відліку О визначається радіусом-вектором \(\vec{r}\) (рис. 5.1).
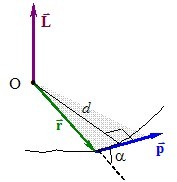
Тоді за означенням
моментом імпульсу частинки відносно даної точки О називається векторний добуток векторів \(\vec{r}\) і \(\vec{p}\):
|
\(\vec{L}=\left[\vec{r}\vec{p}\right] \). |
(1.1) |
|
Числове значення (модуль) моменту імпульсу напрям дорівнює:
|
\( L=rp\sin\alpha=pd \), |
(1.2) |
де α – кут між напрямами векторів \(\vec{r}\) і \(\vec{p}\), а \( d=r\sin\alpha \) – відстань від точки О до лінії вектора \(\vec{p}\), яка називається плечем вектора \(\vec{p}\). Напрям вектора \(\vec{L}\) визначається правилом правого гвинта[1], а сам вектор прийнято розміщувати початком в точці О.
Вектор \(\vec{L}\) є перпендикулярний до площини векторів \(\vec{r}\) і \(\vec{p}\), тобто, до площини, в якій відбувається рух частинки. Тому при русі частинки по плоскій траєкторії
напрям вектора моменту імпульсу частинки визначає орієнтацію площини її траєкторії в просторі.
Рівняння моментів для частинки. Зрозуміло, що сили, які діють на частинку (матеріальну точку), змінюють не лише її імпульс, а й момент імпульсу. Аби з’ясувати, як саме, знайдемо похідну по часу від вектора моменту імпульсу[2] \(\vec{L}\):
|
\(\frac{\mathrm{d}\vec{L}}{\mathrm{d}t}=\left[\frac{\mathrm{d}\vec{r}}{\mathrm{d}t},\vec{p}\right]+\left[\vec{r},\frac{\mathrm{d}\vec{p}}{\mathrm{d}t}\right] \). |
Похідна \(\mathrm{d}\vec{r}/\mathrm{d}t=\vec{v}\) – це швидкість частинки. Тому, позаяк вектори \(\vec{v}\) і \(\vec{p}=m\vec{v}\) є збіжними за напрямом, перший доданок дорівнює нулю. У друому доданку \(\frac{\mathrm{d}\vec{p}}{\mathrm{d}t}=\vec{F}\) – сила, що діє на частинку, тож
|
\(\frac{\mathrm{d}\vec{L}}{\mathrm{d}t}=\left[\vec{r},\vec{F}\right] \). |
Звідси видно, що зміна моменту імпульсу частинки в часі визначається не безпосередньо силою, що діє на неї, а величиною
|
\(\vec{M}=\left[ \vec{r},\vec{F} \right]\), |
(1.3) |
яка називається моментом сили \(\vec{F}\) відносно заданої точки \(\vec{r}\) (початку відліку) і вимірюється в ньютон-метрах (\(\text{Н}\cdot \text{м}\)).
Таким чином,
швидкість зміни моменту імпульсу частинки дорівнює моментові сили, що діє на неї:
|
\(\frac{d\vec{L}}{dt}=\vec{M}\) |
(1.4) |
З рівняння (1.4) випливає також, що
|
\(\mathrm{d}\vec{L}=\vec{M}\mathrm{d}t\), |
де величина в правій частині називається імпульсом моменту сили за проміжок часу dt.
Отже,
зміна моменту імпульсу частинки дорівнює імпульсові моменту сил, що діють на неї.
Зміна моменту імпульсу частинки за скінченний проміжок часу \(\left[t_1,\,\,t_2\right] \) визначається інтегруванням елементарних змін \(\mathrm{d}\vec{L}\):
|
\(\Delta\vec{L}=\vec{L}_2-\vec{L}_1=\int\limits_{t_1}^{t_2}\vec{M}(t)\mathrm{d}t \). |
(1.5) |
Рівняння (1.4), і (1.5) називаються рівняннями моментів. Як за змістом, так і за формою вони є аналогами відповідних рівнянь другого закону Ньютона (див. Розділ ІІ, п.1), причому роль імпульсу відіграє момент імпульсу, а роль сили – момент сили. Зауважимо, що
рівняння моментів можна використовувати і в неінерціальних системах відліку, якщо крім моментів сил взаємодії враховувати й моменти сил інерції.
Момент сили. Момент сили через рівняння (1.4) визначає момент імпульсу частинки в кожен момент часу. Тож варто перелічити основні властивості вектора \(\vec{M}\), що випливають із означення (1.3):
– напрям вектора моменту сили визначається правилом правого гвинта (див. рис. 5.2), а модуль дорівнює
|
\( M=rF\sin\alpha=l F \), |
(1.6) |
де відстань l = rsinα від лінії дії до початку відліку О називається плечем сили \(\vec{F}\).
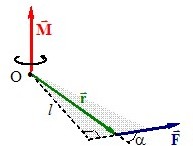
– Момент центральної сили відносно силового центра дорівнює нулю.
– Момент сили не змінюється при перенесенні вектора сили уздовж його лінії[3] (рис. 5.3а).
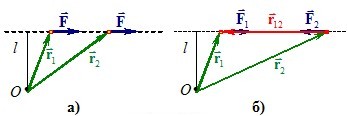
|
\(\vec{M}=\vec{M}_1+\vec{M}_2=\left[\vec{r}_1,\vec{F}_1\right]+\left[\vec{r}_2,\vec{F}_2\right]=\left[\left(\vec{r}_1-\vec{r}_2\right),\vec{F}_1\right]=\left[\vec{r}_{12},\vec{F}_1\right]=0 \). |
(1.7) |
1. 2. Загальні рівняння динаміки системи
Рівняння моментів для системи. Момент імпульсу, як і імпульс, є адитивною величиною і для системи частинок дорівнює:
|
\(\vec{L}=\sum\vec{L}_{i}\). |
(1.8) |
Рух кожної частинки визначається всіми силами, що діють на неї. Тож, згідно з (1.4), для системи
|
\(\frac{\mathrm{d}\vec{L}}{\mathrm{d}t}=\sum\frac{\mathrm{d}\vec{L}_{i}}{\mathrm{d}t}=\sum\vec{M}_{i}\), |
де \(\vec{L}_i \) – моменти імпульсів окремих частинок відносно заданої точки і \(\vec{M}_i \) – моменти (відносно тієї самої точки) всіх сил, які діють на окрему частинку. При цьому повний момент сил можна подати, як суму моментів внутрішніх та зовнішніх сил:
\(\sum\vec{M}_{i}=\sum\vec{M}_{i}\)вн + \(\sum\vec{M}_{i}\)зовн.
Оскільки в будь-якій системі повний момент внутрішніх сил є сумою моментів сил взаємодії між кожною парою частинок, то, згідно з (1.7), перший доданок у цьому виразі дорівнює нулю. Відтак маємо наступне рівняння моментів для системи матеріальних точок:
|
\(\frac{\mathrm{d}\vec{L}}{\mathrm{d}t}=\vec{M}\)зовн |
(1.9) |
де
\(\vec{M}\)зовн = \(\sum\vec{M}_{i}\)зовн.
Таким чином,
швидкість зміни моменту імпульсу довільної системи відносно даної точки дорівнює повному (сумарному) моменту зовнішніх сил, що діють на тіла системи, відносно тієї самої точки.
Відповідно,
зміна моменту імпульсу системи за заданий проміжок часу визначається імпульсом моменту зовнішніх сил за цей проміжок:
|
\( \mathrm{d}\vec{L}=\vec{M}\)зовн\( {\mathrm{d}t}\) |
(1.9а) |
|
|
\(\Delta \vec{L}={{\vec{L}}_{2}}-{{\vec{L}}_{1}}=\int\limits_{{{t}_{1}}}^{{{t}_{2}}}{\vec{M}{{\left( t \right)}_{}}dt}\) |
(1.9б) |
Загальні рівняння динаміки системи. Рівняння моментів, записане відносно початку системи відліку, є одним із основних рівнянь динаміки, так що загальну інформацію про рух довільної системи можна отримати або за законом зміни імпульсу (розділ ІІІ, рівняння (1.1)), або за допомогою рівняння моментів (1.9). Але часто застосовують обидва способи разом[1], використовуючи рівняння руху центра мас системи (розділ ІІІ, рівняння (2.5а)) та рівняння моментів (1.9) відносно центра мас:
|
\( m\vec{a}_c=\vec{F}\), |
||
|
\(\frac{\mathrm{d}\vec{L}}{\mathrm{d}t}=\vec{M} \), |
1.3. Закон збереження моменту імпульсу
У розділі ІІІ (п.1) говорилося, що в замкнених системах виконується закон збереження імпульсу. Це саме стосується і моменту імпульсу. Справді, якщо система замкнена, то в ній всі \(\vec{F_i}\)зовн = 0, отже й \(\vec{M}_{i}\)зовн = 0. Тоді з рівняння моментів (1.9) маємо:
|
\(\frac{d\vec{L}}{dt}=0\quad \Rightarrow \quad \vec{L}=\sum{{{L}_{i}}=\const}\), |
(1.10) |
тобто, закон збереження моменту імпульсу:
момент імпульсу замкненої системи зберігається, тобто, не змінюється з часом.
При цьому моменти імпульсу окремих частинок, звичайно, можуть змінюватися внаслідок взаємодії з іншими частинками системи. Але ці зміни мають характер обміну, так що повний момент імпульсу системи лишається незмінним. Наочне уявлення про прояв закону збереження моменту імпульсу можна одержати, подивившись відеофільм.
Слід зазначити, що момент імпульсу може зберігатись і в незамкненій системі (\(\vec{F}_i \)повн ≠ 0) за умови, що зовнішні сили або не створюють моментів (\(\vec{M}_i \)зовн = 0), або сума цих моментів дорівнює нулю[4]. Прикладом може слугувати збереження моменту імпульсу планет сонячної системи, позаяк зовнішні сили, що діють на них з боку Сонця, є центральними і не створюють моментів. Оскільки лінії дії сил всесвітнього тяжіння проходять через центри мас планет, вони не створюють обертальної дії і не змінюють моментів імпульсу космічних тіл відносно їхніх центрів мас. Одним із наслідків цього є незмінність просторової орієнтації площин орбіт планет та орієнтації осей їхнього добового обертання [5].
Наостанок зауважимо, що за логікою наведеного розгляду закон збереження моменту імпульсу випливає з рівняння моментів (1.8), тобто постає як наслідок основних законів динаміки. Але насправді закон збереження моменту імпульсу, як і закон збереження імпульсу (розділ IІІ, п. 1), є фундаментальним фізичним законом. Зокрема, він виконується і в немеханічних системах, таких як електромагнітне випромінювання, атоми, ядра, тощо.
1. Що називається моментом імпульсу частинки та системи частинок відносно точки?
2. Частинка маси m, що лежить на осі ОZ у точці \({z=l}\), починає рухатися паралельно до осі ОХ із заданим сталим прискоренням \(\vec{a}=a\vec{i}\). Записати вираз вектора моменту імпульсу \(\vec{L}\) частинки відносно початку координат і модуля L цього вектора як функції часу.
3. Відомо, що сума імпульсів усіх частинок системи відносно центра мас дорівнює нулю. Чи стосується це й моменту імпульсу?
4. Що називається моментом сили відносно точки? Від чого залежить модуль цього вектора?
5. Дві антипаралельні сили однакової величини називаються парою сил. Довести, що момент пари сил не залежить від положення точки, відносно якої він визначається. Від чого залежить модуль моменту пари сил?
6. Сума всіх внутрішніх сил у будь-якій системі дорівнює нулю. Чи це так і для суми моментів цих сил?