ФІЗИКА ДЛЯ БАКАЛАВРІВ. МЕХАНІКА
ІV. РОБОТА ТА ЕНЕРГІЯ
2. Кінетична і потенціальна енергія
Наявність енергії в системі тіл є зумовлена їхнім рухом і взаємодією між собою та зовнішніми тілами. Відповідно, механічна енергія поділяється на кінетичну (енергію руху) та потенціальну (енергію взаємодії). Далі розглянуто питання:
2.3. Зв’язок між потенціальною енергією і силою
Теорема про кінетичну енергію. Позаяк при русі частинки під дією сили змінюється її швидкість, існує зв’язок між механічною роботою та станом руху частинки. Розглянемо роботу сумарної (рівнодійної) сили \(\vec{F}\), яка діє на частинку маси m, на елементарному переміщенні \(\mathrm{d}\vec{s}\) по довільній траєкторії (формула (1.1)):
\(\delta{A}=\vec{F}\mathrm{d}\vec{s}\).
Урахувавши, що \(\vec{F}=m\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}\) і \(\mathrm{d}\vec{s}=\vec{v}\mathrm{d}t \) (\(\vec{v} \) – швидкість частинки), отримаємо:
\(\delta{A}=m\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}\vec{v}\mathrm{d}\vec{v}=m\vec{v}\mathrm{d}\vec{v} \).
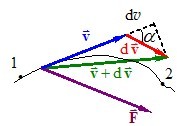
У загальному випадку вектори \(\vec{v}\) і \(\mathrm{d}{\vec{v}}\) не збігаються за напрямом (рис. 4.3), тому
\(\vec{v}\mathrm{d}\vec{v}=v|\mathrm{d}\vec{v}|\cos\alpha=v\mathrm{d}v \).
Примітка. Цей результат є однією з важливих тотожностей векторної алгебри: скалярний добуток вектора на його зміну дорівнює добутку модуля цього вектора на зміну його модуля.
Отже,
\(\delta{A}=mv\mathrm{d}v=\mathrm{d}\left(\frac{mv^2}{2}\right) \).
Бачимо, що елементарна робота дорівнює приростові (зміні) величини
|
\( K=\frac{mv^2}{2} \). |
(2.1) |
Через імпульс тіла p = mv вона визначається, як
|
\( K=\frac{p^2}{2m} \). |
(2.1а) |
Величина К називається кінетичною енергією частинки. Очевидно, що вона вимірюється у джоулях (Дж).
Таким чином, маємо:
|
\(\delta{A}=\mathrm{d}K \). |
(2.2) |
Проінтегрувавши цей випаз уздовж траєкторії від початкової точки 1 до кінцевої точки 2, дістанемо :
|
\( A=K_2-K_1 \) або \( A=\Delta{K} \). |
(2.2а) |
Отримані співвідношення (2.2) і (2.2а) виражають теорему про кінетичну енергію:
зміна кінетичної енергії тіла на будь-якому переміщенні дорівнює роботі всіх сил, які діють на нього на цьому переміщенні.
Слід наголосити на тому, що зв’язок між роботою та кінетичною енергією, є універсальнимспіввідношення (2.2) і (2.2а), які виражають и: вони не залежать від природи та походження сил, які діють на частинку. Зокрема, в неінерціальних системах відліку величина \(\vec{F} \) включає й сили інерції. Але при цьому не слід забувати, що йдеться про повну роботу всіх сил. До прикладу, коли ми рівномірно тягнемо санки за мотузку, то виконуємо роботу, проте кінетична енергія санок не змінюється. Але це зовсім не суперечить теоремі про кінетичну енергію, бо таку саму по модулю від’ємну роботу виконують сили тертя, і повна робота всіх сил дорівнює нулю.
Кінетична енергія системи. Розглянемо тепер зв’язок між роботою й станом руху для довільної системи частинок. Оскільки робота є адитивною величиною, повна робота всіх сил, що діють у системі, дорівнює сумі робіт \( A_i \), які виконуються силами, що діють на кожну частинку системи. Тому, враховуючи співвідношення (2.8) і (2.3), маємо:
\( \delta{A}=\sum_{i}\delta{A}_{i}=\sum_{i}\mathrm{d}K_{i}=\mathrm{d}\left(\sum_{i}K_{i}\right)=\mathrm{d}{K}\),
де величина
|
\( {K}=\sum_{i}K_{i}=\sum_{i}\frac{m_{i}v_{i}^{2}}{2}=\sum_{i}\frac{p_{i}^{2}}{2m_{i}}\) |
(2.3) |
–кінетична енергія системи, котра, як видно, теж є адитивною величиною.
Отже, універсальний зв’язок між кінетичною енергією та роботою сил (2.2) і (2.2а) – теорема про кінетичну енергію – є чинною для довільної системи.
2.2.1. Консервативні та неконсервативні сили
Зміна кінетичної енергії тіла не залежить від природи сил, які виконують надним роботу. Але цього не можна сказати про саму роботу. Розглянемо декілька прикладів.
Робота постійної сили. Нехай на тіло, що переміщується по довільній траєкорії від точки 1 до точки 2 (рис. 4.4) діє незмінна за величиною та напрямом сила \(\vec{F}=\mathrm{const} \).
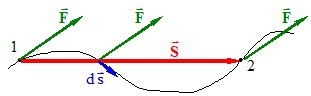
У такому разі із загального виразу (1.3) випливає, що її робота дорівнює
\( A=\int\limits_1^2\vec{F}\mathrm{d}\vec{s}=\vec{F}\int\limits_1^2\mathrm{d}\vec{s} \).
У цьому виразі останній інтеграл є сумою послідовності елементарних векторів \(\mathrm{d}\vec{s}\), розміщених вздовж траєкторії. За правилом додавання векторів ця сума являє собою вектор переміщення \(\vec{S}\) частинки від точки 1 до точки 2: \(\int\limits_1^2\mathrm{d}\vec{s}=\vec{S}\). Отже, робота
|
\( A=\vec{F}\cdot\vec{S}=FS\cos\alpha=FS_{F} \), |
(2.4) |
де SF – проекція вектора \(\vec{S}\) на напрям сили.
Очевидно, що вектор \(\vec{S}\) не залежить від форми траєкторії, що з’єднує точки 1 і 2. Таким чином,
робота сталої сили не залежить від траєкторії переміщення тіла й визначається тільки його початковим та кінцевим положенням.
Робота центральної сили. Центральною називається прикладена до тіла сила, напрям якої весь час проходить через одну й ту саму точку О ("силовий центр"), а величина залежить тільки від відстані до неї (рис. 4.5).
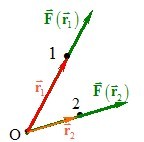
Для такої сили можна записати наступний загальний вираз:
|
\(\vec{F}=F_r(r)\vec{e}_r \), |
(2.5) |
де \(\vec{e}_r \) – орт (одиничний вектор), який указує напрям радіуса-вектора \(\vec{r}\) тіла відносно силового центра, \( F_r(r) \) – проекція сили на напрям \(\vec{r}\), \( r=|\vec{r}|\) – відстань від тіла до силового центра.
З урахуванням (2.11) і (2.2), для роботи центральної сили при переміщенні тіла по довільній траєкторії від точки 1 до точки 2 (рис. 4.6) маємо:
\( A=\int\limits_1^2\vec{F}\mathrm{d}\vec{s}=\int\limits_1^2F_r (r)\vec{e}_r\mathrm{d}\vec{s}=\int\limits_1^2 F_r (r)\mathrm{d}s\cdot\cos\alpha \).
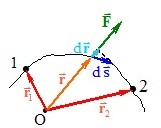
З рис. 4.6 видно, що величина ds·cosα дорівнює dr – зміні відстані від тіла до силового центра. Отже,
|
\( A=\int\limits_1^2 F_r (r)\mathrm{d}r \). |
(2.6) |
Прикметно, що в цьому виразі фігурує не радіус-вектор тіла \(\vec{r}\), який визначає його положення на траєкторії, а лише відстань r до силового центра. Це означає, що, як і у випадку сталої сили,
робота центральної сили не залежить від траєкторії руху тіла.
Сили, робота котрих не залежить від траєкторії руху тіла і визначається тільки його початковим та кінцевим положенням, називаються консервативними силами.
У результаті переміщення по замкненій траєкторії положення тіла в просторі не змінюється, отже,
робота консервативної сили на замкненій траєкторії дорівнює нулю.
Це твердження теж можна розглядати як означення поняття “консервативна сила”.
Конкретними прикладами крнсервативних сил є розглянуті в розділі ІІ сила гравітаційної взаємодії між космічними тілами (2.1) та сила тяжіння (2.2), що діє на тіла біля поверхні планет, а також пружна сила (2.3), що виникає при розтязі еластичного шнура із закріпленим кінцем. До цього переліку можна додати силу електричної взаємодії між зарядженими кульками та силу, шо діє на заряджену кульку між пластинами конденсатора, але вони традиційно в механіці не розглядаються.
Неконсервативні сили. Консервативними є не всі сили, тому решту називають неконсервативними силами. Розглянемо, до прикладу, роботу сили тертя \(\vec{F}\)т при переміщенні бруска маси m по горизонтальній поверхні з коефіцієнтом тертя μ під дією деякої сили \(\vec{F}\) (рис. 4.7).
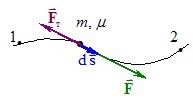
Сила тертя в кожній точці траєкторії напрямлена протилежно до переміщення і в даному випадку має модуль Fт = μmg. Тож її робота на будь-якій ділянці траєкторії визначається пройденим шляхом s :
\( A=-\mu{mg}\int\limits_1^2\mathrm{d}s=-\mu{mgs}\),
зокрема, при русі по замкненій траєкторії – її довжиною. Тож сила тертя є очевидно є неконсервативною. Те саме стосується й сили \(\vec{F}\), яка забезпечує рух бруска, або, до прикладу, сили тиску повітря на вітрила яхти.
Серед усіх неконсервативних сил вирізняють так звані гіроскопічні та дисипативні сили. Гіроскопічними називають сили, що весь час спрямовані перпендикулярно до напрямку руху тіла, на яке діють. Через це
гіроскопічні сили взагалі не виконують роботи.
Такими, зокрема, є коріолісова сила інерції (див. Розділ І, п.3) і сила, що діє на рухомий заряд у магнітному полі (сила Лоренца).
До дисипативних сил відносяться різноманітні сили тертя та опору. Характерною властивістю таких сил є те, що вони завжди спрямовані протилежно до відносних швидкостей взаємодіючих тіл.
Сказане, одначе, не стосується руху тіл відносно заданої системи відліку. У такому разі дисипативні сили можуть не тільки гальмувати рух, а й забезпечувати його. До прикладу, якщо по дошці, що знаходиться на гладкій поверхні, тягти з тертям невеликий брусок (рис. 4.8), то буде рухатися й дошка.
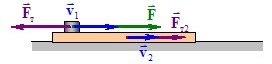
При цьому сила тертя \(\vec{F}\)т2, що діє на дошку, забезпечує її рух і виконує додатню роботу. Але
повна робота дисипативних сил взаємодії між частинками будь-якої системи є завжди від’ємною.
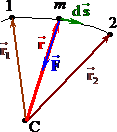
Доведемо це. Нехай між двома частинками 1 і 2, що знаходяться в точках \(\vec{r}_1 \) і \(\vec{r}_2 \) заданої системи відліку і мають швидкості \(\vec{v}_1 \) і \(\vec{v}_2 \), діють дисипативні сили \(\vec{F}_1 \) і \(\vec{F}_2=-\vec{F}_1 \) (третій закон Ньютона), рис. 4.9.
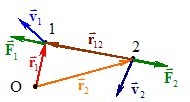
За елементарний проміжок часу dt частинки здійснюють переміщення \(\mathrm{d}\vec{r}_1=\vec{v}_1\mathrm{d}t \) і \(\mathrm{d}\vec{r}_2=\vec{v_2}\mathrm{d}t \) (на рисунку не показані), тож дисипативні сили виконують роботу
\(\delta{A}\)дис = \(\vec{F}_1\mathrm{d}\vec{r}_1+\vec{F}_2\mathrm{d}\vec{r}_2=\vec{F}_1\left(\vec{v}_1-\vec{v}_2\right)\mathrm{d}t=\vec{F}_1\vec{v}_{12}\mathrm{d}t \),
де, згідно із законом перетворення швидкостей (Розділ І, (1.33)), \(\vec{v}_{12}\) – швидкість руху першої частинки відносно другої (відносна швидкість). Оскільки сила \(\vec{F}_1 \) є дисипативною, вона напрямлена протилежно до вектора \(\vec{v}_{12}\), отже|
\(\delta{A}\)дис = \(-F_1v_{12}\mathrm{d}t=-F_1|\mathrm{d}\vec{r}_{12}|<0 \). |
(2.7) |
Якщо сила взаємодії є стала, то
|
\( A \)дис = \(-F_1 \Delta{|\vec{r}_{12}|} \). |
(2.7а) |
Таким чином, за будь-яких умов
сумарна робота дисипативних сил взаємодії між двома частинками є від’ємною і визначається не переміщенням кожної частинки окремо, а лише їхнім відносним переміщенням.
Робота сили тяжіння. Біля поверхні планети сила тяжіння спрямована вертикально вниз і є однорідною: \( m\vec{g}=\mathrm{const} \) (рис. 4.10).
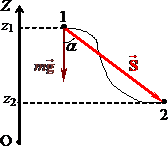
Тому її робота при переміщенні частинки з точки 1 у точку 2 по будь-якій траєкторії, згідно з (2.4), визначається, як
|
\( A=mg\cdot s\cos\alpha=mg\left(z_1-z_2\right)\) \(\Rightarrow \) \( {A}=mg{{z}_{1}}-mg{{z}_{1}}\) |
(2.8) |
де z1 і z2 – початкова та кінцева вертикальна координата частинки.
Робота гравітаційної сили. Із закону всесвітнього тяжіння (Розділ ІІ, (2.8)) випливає, що сила \(\vec{F}\), яка діє на будь-яке тіло m (наприклад, комету) з боку іншого тіла М (приміром, Сонця), є центральною (рис. 4.11).
Проекція сили \(\vec{F}\) на напрям радіуса-вектора тіла \(\vec{r}\) дорівнює Fr = –GMm/r2, тому, згідно з (2.6), її робота при переміщенні тіла від точки 1 до точки 2 по довільній траєкторії дорівнює
|
\( A=\int\limits_1^2F_r(r)\mathrm{d}r=-GMm\int\limits_1^2\frac{\mathrm{d}r}{r_2}\) \( \Rightarrow \) \( {A}=-G\frac{Mm}{r_1}-\left(-G\frac{Mm}{r_2}\right) \). |
(2.9) |
Робота пружної сили. Робота пружної сили \(\vec{F}\) при переміщенні вільного кінця еластичного шнура (або пружини) по довільній траєкторії (рис. 4.12) визначається аналогічно.
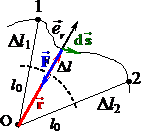
Якщо позначити через l0 довжину недеформованого шнура і через Δl = l – l0 величину його деформації (розтягу), то вектор пружної сили, що діє на незакріплений кінець, згідно з (Розділ ІІ, (2.10)), можна записати як \(\vec{F}=-\vec{e}_r k\Delta{l}\), де k – жорсткість шнура, \(\vec{e}_r \) – орт (одиничний вектор), який вказує напрям радіуса-вектора вільного кінця шнура. В такому разі, згідно з (2.6), отримуємо:
|
\( A=\int\limits_1^2F_r(r)\mathrm{d}r=-k\int\limits_1^2\Delta{l}\cdot\mathrm{d}(\Delta{l}) \) \( \Rightarrow \) \( {A}=\frac{k\Delta{l_1^2}}{2}-\frac{l\Delta{l_2^2}}{2} \) |
(2.10) |
Тут враховано, що проекція сили Fr = –kΔl визначається величиною деформації Δl шнура, а зміна відстані r від вільного кінця шнура до точки О — зміною величини деформації: dr = d(Δl).
З отриманих виразів видно, що робота кожної з розглянутих сил дорівнює спадові[1] певної фізичної величини U, так що
|
\( A=U_1-U_2 \), |
(2.11) |
а для елементарних переміщень,
|
\(\delta{A}=-\mathrm{d}U \). |
(2.11а) |
Ця величира й називається потенціальною енергією. Іншими словами,
потенціальною енергією називається величина, спад якої при переміщенні частинки з однієї точки в іншу дорівнює роботі, що виконується консервативними силами, що діють на частинку при цьому переміщенні.
Порівнюючи вираз (2.11) із виразами (2.8) – (2.10), можна дійти висновку, що потенціальна енергія частинки, котра перебуває під дією сил тяжіння, гравітації, або пружності визначається, відповідно, такими формулами:
|
\( U=mgz \), |
(2.12) |
|
|
\( U=-G\frac{Mm}{r}\), |
(2.13) |
|
|
\( U=\frac{k\Delta{l^2}}{2}\). |
(2.14) |
Ці формули й справді є загальновживаними. Але слід зазначити, що жодне зі співвідношень (2.8) – (2.11а) не зміниться, якщо у формулах (2.12) – (2.14) до величини U додати будь-яке число. Це означає, що однозначно визначеною є не сама потенціальна енергія U, а лишень її зміна ΔU при переміщенні частинки між якимось двома точками. Що ж до величини U, то її можна вказати тільки по відношенню до заздалегідь обраного нульового рівня, тобто — точки (або множини точок), де потенціальна енергія приймається рівною нулю. Це добре видно з формули (2.12), в якій величина z (вертикальна координата) безпосередньо залежить від вибору початку відліку. Так само формула (2.13) визначає гравітаційну потенціальну енергію не “взагалі”, а по відношенню до нескінченно віддаленої точки (адже U = 0 при r → ∞), а формула (2.14) показує, що пружна потенціальна енергія приймається рівною нулю, коли Δl = 0, тобто, за відсутності деформаціїй.
Такий вибір нульових рівнів є природнім, але не обов’язковим. До прикладу, легко показати, що формули (2.12) і (2.13), виражають одну й ту саму енергію, але по відношенню до різних нульових рівнів. Справді, роботу гравітаційної сили при переміщенні тіла біля поверхні Землі можна обчислювати за загальною формулою (2.9):
\( A=-G\frac{mM}{r_1}-\left(-G\frac{mM}{r_2}\right)=GmM\left(\frac{1}{r_2}-\frac{1}{r_1}\right)=\frac{GmM(r_1-r_2)}{r_1 r_2}\),
де m і M – відповідно, маса тіла та Землі, r1 і r2 – відстань від тіла до центра Землі в його початковому та кінцевому положенні. Але, якщо записати r = R + z (R – радіус Землі, z – вертикальна координата тіла, відрахована від земної поверхні), і врахувати, що біля поверхні з великою точністю r1·r2 = R2, отримаємо:\( A=\frac{GmM}{R^2}\cdot(z_1-z_2)=mgz_1-mgz_2 \)
де враховані формули (3.9) і (3.10).
Цей результат збігається з виразом (2.8) і випливає з (2.9) як наслідок зміни вибору нульового рівня потенціальної енергії. Так само при розгляді коливань тягарця, що підвішений на пружині, за нульовий рівень потенціальної енергії пружини зручніше прийняти положення статичної рівноваги тягарця, коли пружина вже має деформацію, спричинену його вагою.
Особливість потенціальної енергії полягає також у тому, що вона, на відміну від кінетичної, є величиною алгебраїчною, тобто може бути як додатньою, так і від’ємною, залежно від характеру діючих сил і вибору нульового рівня.
Поняття про силове поле. Коли ми говоримо, що тіло має певну потенціальну енергію, то це не зовсім точно. Наявність у тіла потенціальної енергії спричинюється дією на нього консервативної сили з боку якогось іншого тіла (чи тіл). Але за третім заоном Ньютона дане тіло діє на друге з такою самою силою і “надає” йому такої самої потенціальної енергії. Тому обидва тіла є рівноправними партнерами по взаємодії, і слід говорити не про потенціальну енергію даного тіла, а про енергію взаємодії даної пари тіл. Це яскраво демонструє формула (2.13), що сама по собі не дозволяє сказати, якому з тіл "належить" гравітаційна енергія U.
Але часто характеристики взаємодіючих тіл дуже сильно відрізняються, як, до прикладу, у випадку каменя й Землі. Тоді дія одного тіла ніяк не впливає на стан іншого (Землі), і останнє розглядають не як партнера по взаємодії, а як джерело силового поля, в якому перебуває перше. Відповідно, говорять не про потенціальну енергію взаємодії каменя й Землі, а про потенціальну енергію каменя в гравітаційному полі Землі, в кожній точці якого на тіло діє визначена сила тяжіння. Так само говорять про “поле сил пружності” деформованого (реально чи віртуально) еластичного шнура чи пружини із закріпленим одним кінцем, тощо.
Отже, узагальнюючи, можна сказати, що, якщо в кожній точці заданої області простору на тіло діє визначена сила, то в цій області існує силове поле. При цьому поля можуть утворюватися різними силами, але тільки для консервтивних сил їх можна характеризувати не тільки силою, а й потенціальною енергією. Тому
поля консервативних сил називаються потенціальними полями.
Потенціальна енергія системи. Серед консервативних сил, які діють на частинки системи, можуть бути як зовнішні (сили зовнішніх потенціальних полів), так і внутрішні (сили взаємодії частинок між собою). Тому потенціальну енергію системи U поділяють на зовнішню Uз (енергію в зовнішньому полі) і внутрішню або власну Uв , так що повна потенціальна енергія системи
|
U = Uз + Uв. |
(2.15) |
Зовнішня потенціальна енергія визначається співвідношенням (2.11) через сумарну роботу всіх зовнішніх консервативних сил :
|
\( {A}=\sum{{{A}_{i}}}=\sum{{{U}_{1}}_{i}}-\sum{{{U}_{2}}_{i}}\quad \Rightarrow \quad {{U}_{3}}=\sum{{{U}_{i}}}\) |
У цьому виразі Ui – потенціальні енергії окремих частинок системи в зовнішньому полі. Отже, зовнішня потенціальна енергія системи є адитивною величиною. Але цього не можна сказати про власну, відтак і повну потенціальну енергію системи. Справді, нехай дві системи із власними потенціальними енергіями Uв1 і Uв2 об’єднуються в одну, як схематично показано на рис. 4.13:
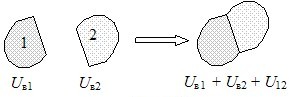
Uв = Uв1 + Uв2 + U12,
де U12 – енергія взаємодії між частинами об’єднаної системи, рівна роботі, що була виконана силами взаємодії в процесі об’єднання.
Оскільки роботу консервативної сили можна знайти як безпосередньо через силу, так і через потенціальну енергію, між цими величинами існує прямий зв’язок. Розглянемо роботу ΔA довільної консервативної сили \(\vec{F}\) на невеликому переміщенні \(\Delta{\vec{S}}\) (рис. 4.14).
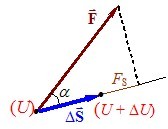
Наближено вона визначається як \( A\approx\vec{F}\cdot\Delta{\vec{S}}=F\cdot\Delta{S}\cos\alpha=F_S\Delta{S}\)[2], звідки \( F_s\approx\frac{\Delta{A}}{\Delta{S}}\). Але, відповідно до співвідношення (2.17), \( A=-\Delta{U}\), тож \( F_s\approx-\frac{\Delta{U}}{\Delta{S}}\). Точний вираз отримаємо у границі ΔS → 0:
| \({{F}_{S}}=-\lim \frac{\Delta U}{\Delta S}\) |
(2.16) |
Така границя в математиці позначається як \(\frac{\partial{U}}{\partial{S}}\) і називається похідною функції U за напрямом S. Вона показує швидкість зміни величини U при переміщенні в заданому напрямку S. Отже, враховуючи цю символіку, можемо записати:
|
\( F_s=-\frac{\partial{U}}{\partial{S}}\) |
(2.17) |
тобто,
проекція консервативної сили на будь-який напрям дорівнює взятій з протилежним знаком похідній потенціальної енергії в цьому напрямі.
Знак “–” у виразі (2.17) означає, що сила спрямована в бік зменшення потенціальної енергії і є тим більшою, чим швидше зменшується потенціальна енергія в цьому напрямі.
Загальний вираз (2.17) дозволяє визначити й проекції сили на координатні осі[3]:
\({{F}_{x}}=-\frac{\partial U}{\partial x},\quad {{F}_{y}}=-\frac{\partial U}{\partial y},\quad {{F}_{z}}=-\frac{\partial U}{\partial z},\)
а відтак і вектор сили, як
|
\(\vec{F}=-\left(\vec{i}\frac{\partial{U}}{\partial{x}}+\vec{j}\frac{\partial{U}}{\partial{y}}+\vec{k}\frac{\partial{U}}{\partial{z}}\right) \). |
(2.18) |
Потреба в подібних операціях в математиці та фізиці виникає доволі часто, тому вираз у дужках (2.18) має свою назву й позначення. Він називається градієнтом потенціальної енергії[4] і позначається символом gradU:
|
\(\mathrm{grad}U=\left(\vec{i}\frac{\partial{U}}{\partial{x}}+\vec{j}\frac{\partial{U}}{\partial{y}}+\vec{k}\frac{\partial{U}}{\partial{z}}\right) \). |
(2.19) |
Таким чином, зв’язок між силою, та потенціальною енергією записується у вигляді:
|
\(\vec{F}=-\mathrm{grad}U \), |
(2.20) |
тобто,
консервативна сила, що діє на частинку, дорівнює взятому з протилежним знаком градієнту потенціальної енергії цієї частинки.
У математиці доводиться, що вектор градієнта даної функції напрямлений у бік її найшвидшого зростання й по модулю дорівнює цій швидкості. Тому
будь-яка консервативна сила спрямована в бік найшвидшого зменшення потенціальної енергії.
Зокрема із цієї причини, вода під дією сили тяжіння стікає по лінії найбільшої крутизни схилу.
1. Що визначають кінетична та потенціальна енергія тіла?
2. Який загальний зв’язок існує між роботою сил і кінетичною енергією?
3. Коли брусок рівномірно тягнуть за нитку по столу, то виконують певну роботу. Чому ж не змінюється кінетична енергія бруска?
4. Як розрізняють сили за критерієм роботи?
5. Які сили називаються консервативними? Наведіть приклади.
6. Чому дорівнює робота консервативної сили на замкненому шляху? Доведіть це шляхом аналізу їхньої роботи на різних ділянках траєкторії.
7. Дайте означення поняття “потенціальна енергія” та перелічіть її загальні властивості.
8. Які сили називаються дисипативними? Чим вони відрізняються від інших сил?
9. Що таке “гіроскопічні сили”? Наведіть приклали.
10. Потенціальна енергія mgh є результатом взаємодії тіла із Землею. Чому ж цю величину називають енергією тіла, а не енергією системи тіло – Земля, як, здавалося б, мало бути?
11. Протяжне тверде тіло складається з безлічі жорстко зв’вязані малих часточок. Чому тоді в механіці не враховується взаємодія між ними?
[1] Спадом називають різницю між початковим і кінцевим значенням змінної величини; спад дорівнює взятому з протилежним знаком приростові (зміні) величини. Слід також зазначити, що терміни “приріст” і “спад” не слід трактувати дослівно, як “збільшення” і “зменшення”, адже кожна з цих величин, залежно від умов, може виявитись як додатньою, так і від’ємною
[2] Його неточність зумовлена тим, що в різних точках навіть невеликого переміщення сила може мати відмінні значення.
[3] При цьому елементарні переміщення вздовж координатних осей є нескінченно малими приростами (диференціалами) координат – аргументів функції потенціальної енергії U = U(x, y, z). Тому похідна по кожному з напрямків x, y, z визначається за звичайними правилами диференціювання, але дві інші координати при цьому розглядаються як константи.
[4] Зрозуміло, що поняття градієнта відноситься й до інших величин, які є функціями координат.