ФІЗИКА ДЛЯ БАКАЛАВРІВ. МЕХАНІКА
ІV. РОБОТА ТА ЕНЕРГІЯ
1. Робота і потужність сили
У загальному вжитку термін робота має досить широкий зміст. Але, в науці візична величина робота є кількісною характеристикою взаємних перетворень енергії. Далі розглянуто:
Механічна робота характеризує дію заданої сили на заданій траєкторії руху тіла і має наступне означення.
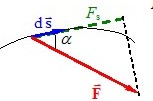
Елементарною роботою \(\delta A\) сили \(\vec{F} \) на нескінченно малому переміщенні \(\mathrm{d}\vec{s} \) називається величина:
|
\(\delta{A}=\vec{F}\mathrm{d}\vec{s}=F\mathrm{d}s\cos\alpha=F_s\mathrm{d}s \), |
(1.1) |
тобто, – скалярний добуток векторів сили та переміщення. У наведених виразах \(\mathrm{d}s=|\mathrm{d}\vec{s}| \) – елементарний шлях і \( F_s=F\cos\alpha \) – проекція вектора сили на напрям вектора переміщення (див. рис. 4.1).
Примітка. Тут і далі для елементарної роботи використовується позначення \(\delta A\), а не звичне dA. Так зроблено, аби відтінити те, що \(\delta A\) є “малою порцією” роботи, а не її приростом унаслідок зміни іншої величини, від якої величина А функціонально залежить.
З означення (1.1) випливають такі загальні властивості роботи сили.
1) Робота є алгебраїчною величиною, тобто може мати той, чи інший знак, залежно від кута α. Зокрема, коли він тупий, робота сили від’ємна. Інакше говорячи, від’ємну роботу виконує сила, що напрямлена проти переміщення, тож спричинює гальмівну дію. Зрозуміло, що в цьому випадку переміщення тіла здійснюється або за рахунок якоїсь іншої сили, або за рахунок інерції руху. Тому буває зручніше замість роботи гальмівної сили \(\delta A\) < 0, розглядати додатню величину \(\delta A\)′ = - \(\delta A\) – роботу, що виконується тілом проти цієї сили. Й нарешті, коли сила є перпендикулярна до переміщення, то в (1.1) cosα = 0, і сила роботи не виконує.
2) Робота рівнодійної декількох сил \(\vec{F}=\sum{{{{\vec{F}}}_{i}}}\) на даному переміщенні \(d\vec{r}\) дорівнює сумі робіт кожної з них:
|
δА = \(\vec{F}d\vec{r}=\left( \sum{{{{\vec{F}}}_{i}}} \right)d\vec{r}=\sum{\left( {{{\vec{F}}}_{i}}d\vec{r} \right)}=\sum{\delta {{A}_{i}}}\) |
(1.2) |
3) Дослід свідчить, що робота є адитивною величиною: при переміщенні тіла по траєкторії на скінчену відстань робота на всій траєкторії дорівнює сумі робіт, які виконуються на всіх її ділянках. Тому робота при переміщенні тіла по траєкторії із заданої точки 1 у задану точку 2 у загальному випадку визначається як криволінійний інтеграл[1] від виразу (1.1):
|
\( A=\int\limits_1^2\vec{F}\mathrm{d}\vec{s}=\int\limits_1^2 F_s \mathrm{d}s \). |
(1.3) |
Ураховуючи геометричний зміст інтеграла, роботу можна знаходити з графіка залежності \( F_s\mathrm{d}s \): площа під відповідною його ділянкою (виділена на рис. 4.2) чисельно дорівнює виконаній роботі.
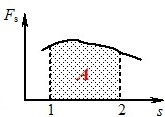
При русі вздовж прямої під дією сталої за величиною й напрямом сили, що діє під кутом \(\alpha \) до напрямку руху, величина Fs = F cosα = const, і вираз (1.2) дає:
|
\( A=\int\limits_1^2 F_s\mathrm{d}s=F_s\int\limits_1^2\mathrm{d}s=F_s{s}\) \( \Rightarrow \) \( {A}=Fs\cos\alpha \). |
(1.4) |
Якщо сила діє в напрямку руху (\(\alpha \) = 0), то A = Fs. На основі цього встановлюється одиниця роботи джоуль (Дж): 1 Дж = 1 Н·м.
З практики добре відомо, що ефективність механізмів і машин (наприклад, двигунів) визначається не величиною виконуваної роботи, а тим як швидко вони здатні її виконувати. Інтенсивність виконання роботи характеризується потужністю, яка визначається величиною роботи за одиницю часу й вимірюється у ватах (Вт): 1 Вт = 1 Дж/с. Якщо інтенсивність виконання роботи змінюється з часом, то розрізняють середню та миттєву потужності.
Середня потужність – це відношення роботи А до тривалості проміжку часу t, за який вона виконана:
|
\(\langle P\rangle=\frac{A}{t} \). |
(1.5) |
Миттєва потужність характеризує інтенсивність виконання роботи в кожен момент часу й визначається виразом:
|
\( P=\frac{\delta{A}}{\mathrm{d}t} \), |
(1.5а) |
|
\( P=\vec{F}\cdot\vec{v}=Fv\cos\alpha \), |
(1.6) |
де \(\alpha \) - кут між векторами \(\vec{F}\) та \(\vec{v}\).
Зазначимо, що, на відміну від побуту та техніки, в теорії потужність сили розглядається як алгебраїчна величина, знак якої збігається зі знаком роботи сили і залежить від прискорюючої, чи гальмівної дії цієї сили.
1. Що називається механічною “роботою” та який зміст має ця фізична величина?
2. Тіло масою m, кинуте вертикально, піднялося на висоту h і впало. Яку роботу воно виконало під час підйому та під час падіння?
3. Переносячи відро води, людина прикладає до нього вертикальну силу, яка, згідно з формулою (1.4), на горизонтальному шляху не виконує роботи. Чому ж тоді людина стомлюється, причому навіть тоді, коли стоїть на місці?
4. Як обчислюється робота сили на траєкторії довільної форми?
5. Тіло пройшло половину кола радіуса R під дією сил, серед яких була й задана стала сила F, спрямована під кутом 60° до відрізка, що з’єднує крайні точки траєкторії. Яку роботу виконала ця сила?
6. Який геометричний зміст має робота сили? Чи завжди можна реально визначити роботу за графіком сили?
7. Який зміст має фізична величина “потужність сили” та за якою формулою вона обчислюється при довільному русі тіла?
8. Запишіть вираз і покажіть графік залежності потужності сили тяжіння від часу для тіла, що кинуте під кутом до горизонту.
9. Чому при підйомі авта вгору водій перемикає двигун на нижчу передачу?
[1] Такий інтеграл відрізняється від звичайного тим, що “додаються” не добутки значення функції на приріст аргументу, а добутки вектора сили на нескінченно малі переміщення тіла вздовж певної лінії – траєкторії руху тіла. Відповідно символи в позначенні інтеграла (границі інтегрування) – то є не числа, а позначення початкової та кінцевої точок на траєкторії, вдовж якої обчислюється криволінійний інтеграл.