ФІЗИКА ДЛЯ БАКАЛАВРІВ. МЕХАНІКА
ІІ. ОСНОВНІ ЗАКОНИ ДИНАМІКИ
3. Сили інерції
На практиці рух тіл інколи доводиться розглядати і в неінерціальних системах відліку (НСВ) — системах відліку, які мають прискорення відносно інерціальних систем відліку (ІСВ).
У такому разі закони Ньютона втрачають силу, але основні рівняння динаміки (1.5) і (1.7) можна модифікувати так, аби вони зберігали чинність і в НСВ. Для цього в них, окрім сил взємодії, треба включати й так звані сили інерції, які розглядаються в наступних питаннях:
3.1. Сили інерції в поступальній НСВ
3.2. Сили інерції в обертовій системі відліку
3.3. Загальне рівняння руху тіла в НСВ
3.1. Сили інерції в поступальній НСВ
Згадаймо добре відому кожному ситуацію. В автобусі, що рухається без прискорення, ми перебуваємо відносно нього в спокої і відчуваємо лише силу реакції опори (підлоги). Але під час різкого гальмування чи прискорення, або на крутих віражах якась сила відкидає нас прямо, або вбік. Ця сила виникає не тому, що на нас починають діяти якісь інші тіла, а через те, що автобус, який є для нас природньою системою відліку, набуває прискорення відносно Землі, тобто стає неінерціальною системою відліку.
Сили, що зумовлені не взаємодією між тілами, а властивостями системи відліку[1], називаються силами інерції.
Розглянемо рух тіла в системі відліку K′(Х′,О′,Y′) (рис. 2.5), що рухається поступально з прискоренням \(\vec{a}_0 \) вздовж осі ОХ інерціальної системи відліку К(Х,О,Y).
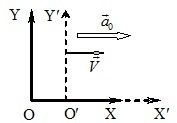
Якщо тіло рухається відносно К-системи зі швидкістю \(\vec{v} \), то за законом додавання швидкостей (розділ І, (1.33)) його швидкість в K′-системі
|
\( \vec{v'}=\vec{v}-\vec{V}, \) |
де \( \vec{V}\) – швидкість K′-системи відносно К-системи. Звідси за означенням прискорення
|
\( \vec{a'}=\vec{a}-\vec{a_0},\) |
(3.1) |
де \( \vec{a'}\) – прискорення тіла в НСВ K′, \( \vec{a}\) – його прискорення в ІСВ К, і \(\vec{a}_0 \) – прискорення K′– системи відліку відносно К.
Помноживши вираз (3.1) на масу тіла т, одержимо
|
\( m\vec{a'}=m\vec{a}-m\vec{a}_0 \). |
(3.1а) |
Величина \( m\vec{a}=\vec{F}\) – то є “звичайна” сила, що діє на тіло в інерціальній системі відліку з боку інших тіл. Але прискорення тіла в НСВ K′ визначається не тільки цією силою, а й величиною
|
\( \vec{F}_i=-m\vec{a}_0, \) |
(3.2) |
яка називається (поступальною) силою інерції. Ця сила зумовлена прискореним рухом НСВ K′ відносно інерціальної К-системи відліку, а не взаємодією даного тіла з якиимось іншими тілами. Тому
для сил інерції третій закон Ньютона не виконується.
Іншою особливістю є те, що
сила інерції визначається добутком маси тіла не на його власне прискорення, а на прискорення системи відліку.
З уведенням сили інерції рівняння (3.1а) набуває вигляду основного рівняння динаміки (1.5), в якому, крім “звичайних сил” фігурує ще й сила інерції:
|
\( m\vec{a'}=\vec{F}+\vec{F}_i \). |
(3.3) |
3.2. Сили інерції в обертовій системі відліку
Прикладом такої НСВ К′ є платформа каруселі, що обертається зі сталою кутовою швидкістю \(\omega \) навколо своєї осі, нерухомої в ІСВ К, зв’язаній із землею. Кожна точка, що перебуває в спокої відносно платформи (в в К′-системі), відносно землі (в К-системі) має доцентрове прискорення, що залежить від швидкості обертання платформи та відстані точки від осі обертання. Тому прискорення тіла в ІСВ К (відносно землі) залежить не тільки від зміни швидкості тіла, а й від його положення в НСВ K′ (відстані до осі обертання платформи). Тому в обертових системах відліку існує два види сил інерції – відцентрова та коріолісова.
Відцентрова сила. Спочатку розглянемо тіло, що перебуває в спокої відносно НСВ К′, яка обертається з кутовою швидкістю \(\omega \) навколо осі О' О'', нерухомої в відносно ІСВ К (рис. 2.6).
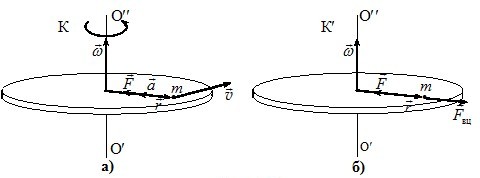
Нехай на поверхні диска лежить тіло, прикріплене до осі обеотання ниткою довжини r. Тоді відносно системи відліку К воно рухається по колу радіуса r із нормальним прискоренням \(\vec{a}= -\omega^2\vec{r}\). Це прискорення створюється силою натягу нитки \(\vec{F}\) (рис. 2.6а), яка за другим законом Ньютона складає \(\vec{F}= -m\omega^2\vec{r}\) . Але відносно диска тіло є нерухомим, отже в системі відліку K′ його прискорення \(\vec{a'}=0 \). Згідно з (3.3), це означає, що в обертовій НСВ на тіло, крім сили взаємодії \(\vec{F}\), діє ще й рівна їй за модулем і протилежна за напрямом сила інерції
|
\( \vec{F}\)вц = \( {m}\omega^{2}\vec{r}\). |
(3.4) |
|
Ця сила напрямлена від осі (центра) обертання системи відліку K′ (рис. 2.6б) і називається відцентровою силою. Саме відцентрову силу відчуває пасажир на поворотах.
Сила Коріоліса. Нехай тепер точка рухається відносно обертової системи відліку K′ із швидкістю \(\vec{v'}\) (рис. 2.7).
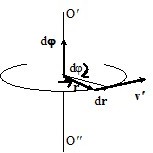
Тоді в інерціальній К-системі відліку за час dt радіус-вектор \(\vec{r}\), який задає положення точки відносно осі обертання, набуде приросту
|
\(\mathrm{d}\vec{r}=\vec{v'}\mathrm{d}t+\left[\mathrm{d}\vec{\varphi},\vec{r}\right]. \) |
(3.5) |
У цьому виразі перший доданок зумовлений рухом точки відносно K′-системи відліку, а другий – то є переміщення точки разом із K′-системою при її повороті на кут \(\mathrm{d}\vec{\varphi}\) відносно К-системи відліку (див. (2.1а)). Поділивши (3.5) на dt, одержимо:
|
\(\vec{v}=\vec{v'}+\left[\vec{\omega},\vec{r}\right]. \) |
(3.5а) |
Суттєво, що \(\vec{v}\) залежить від \(\vec{r}\). Тому, навіть коли точка в обертовій системі відліку K′ рухається рівномірно (\(\vec{v'}=\mathrm{const}\)), її швидкість відносно нерухомої К-системи відліку буде змінюватися внаслідок зміни відстані r до осі О'О''. Тому приріст вектора швидкості \(\mathrm{d}\vec{v}\) у К-системі визначається як зміною вектора відносної швидкості \(\mathrm{d}\vec{v'}\), так і зміною радіуса-вектора \(\mathrm{d}\vec{r}\):
|
\(\mathrm{d}\vec{v}=\mathrm{d}\vec{v'}+\left[\vec{\omega},\mathrm{d}\vec{r}\right]. \) |
(3.6) |
Підставивши в це співвідношення вираз (3.5), отримаємо:
|
\(\mathrm{d}\vec{v}=\mathrm{d}\vec{v'}+\left[\vec{\omega},\vec{v'}\right]\mathrm{d}t+\left[\vec{\omega}\left[\mathrm{d}\vec{\varphi},\vec{r}\right]\right] \) |
(3.7) |
Розглянемо тепер зміну вектора \(\vec{v}\) відносно системи відліку К. Навіть якщо швидкість тіла \(\vec{v'}\) в обертовій системі відліку K′ є сталою, внаслідок повороту системи K′ на деякий кут \(\mathrm{d}\vec{\varphi}\) за час dt, вектор \(\vec{v'}\) відносно К-системи відліку теж повернеться на кут \(\mathrm{d}\vec{\varphi}\) і отримає приріст \(\mathrm{d}\vec{v'}=\vec{a'}\mathrm{d}t+\left[\mathrm{d}\vec{\varphi},\vec{v'}\right] \). Якщо ж тіло має відносно K′- системи відліку ще й прискорення \(\vec{a'}\), то вектор \(\vec{v'}\) набуває додаткового приросту \(\vec{a'}\mathrm{d}t \). Тому в загальному випадку
|
\(\mathrm{d}\vec{v}=\vec{a'}\mathrm{d}t+\left[\mathrm{d}\vec{\varphi},\vec{v'}\right]. \) |
Підставивши цей вираз у (3.7) і поділивши на dt, отримаємо:
|
\(\vec{a}=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}=\vec{a'}+2\left[\vec{ \omega},\vec{v'}\right]+\left[\vec{\omega}\left[\vec{\omega},\vec{r}\right]\right]. \) |
Легко переконатися, що \(\left[\vec{\omega}\left[\vec{\omega},\vec{r}\right]\right]=-\omega^2\vec{r}\). Враховуючи також, що \(\left[\vec{v'},\vec{\omega}\right]=-\left[\vec{\omega},\vec{v'}\right]\), маємо:
|
\(\vec{a'}=\vec{a}+2\left[\vec{v'},\vec{\omega}\right]-\left[\vec{\omega}\left[\vec{\omega},\vec{r}\right]\right]. \) |
(3.8) |
Помноживши цей вираз на масу m точки, одержимо рівняння динаміки матеріальної точки в обертовій системі відліку:
|
\( m\vec{a'}=m\vec{a}+2m\left[\vec{v'},\omega\right]+m\omega^2\vec{r}. \) |
(3.9) |
або
|
\( m\vec{a'}=\vec{F}+\vec{F}\)к + \(\vec{F}\)вц, |
(3.9а) |
де \(\vec{F}=m\vec{a}\) – сила взаємодії точки з іншими тілами, \(\vec{F}\)вц\( =m\omega^2\vec{r}\) – вже знайома відцентрова сила інерції. Але, крім неї, на рухому точку в обертовій системі відліку діє ще одна сила інерції
|
\( \vec{F}_{k}=2m\left[\vec{v}^{\prime},\vec{\omega}\right] \), |
(3.10) |
яка називається силою Коріоліса (або коріолісовою силою). Деякі прояви сили Коріоліса показані у відео.
Характерною властивістю сили Коріоліса є те, що вона завжди діє перпендикулярно до напрямку руху тіла. Зокрема, при русі в меридіональному напрямку в північній півкулі вона напрямлена праворуч по ходу руху тіла, а у південній – ліворуч (рис. 2.8).
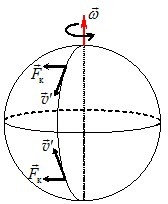
З цим пов’язаний відомий ефект підмивання правих берегів річок у північній півкулі і лівих у південній. Також завдяки коріолісовій силі спостерігається обертання площини коливань математичного маятника. Саме це дозволило у свій час (1852 р.) французькому фізикові Фуко довести, що Земля обертається навколо своєї осі. Існують й інші прояви сил Коріоліса. Зокрема, при русі тіла вздовж паралелі сила Коріоліса має вертикальну складову, напрямлену вгору при русі на схід і вниз при русі на захід, що впливає на дальність польоту тіл і враховується в балістиці.
3.3. Загальне рівняння руху точки в НСВ
У кінематиці (частина І, розділ 2) говорилося про те, що на загал рух твердого тіла можна трактувати як сукупність поступального та обертального рухів. Тому в довільній неінерціальній системі відліку на тіла, крім сил взаємодії, діють усі розглянуті види сил інерції. Відповідно, основні рівняння руху (1.5) і (1.7) у довільній НСВ мають вигляд:
|
\( m\vec{a'}=\vec{F}-m\vec{a}_0+m\omega^2\vec{r}+2m\left[\vec{v'},\vec{\omega}\right]\); |
(3.11) |
|
|
\( \frac{\mathrm{d}\vec{r'}}{\mathrm{d}t^2}=\frac{\vec{F}}{m}-\vec{a}_0+\omega{\vec{r}}+2\left[\vec{v'},\vec{\omega}\right], \) |
(3.12) |
де \(\vec{a}_0 \) і \(\vec{\omega} \) – поступальне прискорення та кутова швидкість системи відліку. Два інші доданки являють собою відцентрове прискорення
|
\( \vec{a}_{вц}=\omega^{2}\vec{r}\) |
(3.13) |
та коріолісове прискорення
|
\(\vec{a}_K=2\left[\vec{v'},\vec{\omega}\right] \). |
|
1. Чи виконуються закони Ньютона в довільній системі відліку?
2. На горизонтальній платформі, що рухається рівномірно і прямолінійно, лежить кулька. Але коли платформа починає рухатися прискорено, кулька теж починає прискорено котитися по платформі. Як це пояснить спостерігач, який перебуває на платформі, та той, хто стоїть на землі?
3. Чим відрізняється рівняння динаміки руху тіла в неінерціальній системі відліку від рівняння його руху в інерціальній системі відліку?
4. Чи скрізь напрям нитки виска збігається з точним напрямом до центра Землі? Якщо ні, то чому і в який бік є відхилена нитка?
5. Чи є різниця між поняттями “прискорення вільного падіння” та “прискорення сили тяжіння”?
6. В якому випадку коріолісова сила інерції, що діє на тіло на поверхні Землі, збігається за напрямом із відцентровою силою?
7. Чи можливо, щоби коріолісова сила, котра діє на тіло, що рухається на південь, теж була напрямлена на південь?
8. На екваторі роблять постріл із гармати один раз точно на північ, а другий – на південь. Що можна сказати про дальність польоту снаряда в обох випадках?
9. З однакової висоти роблять горизонтальний постріл із гармати точно на схід: один раз на екваторі, а інший – десь у північній півкулі. Чим будуть відрізнятися траєкторії снаряда?
[1] З цієї причини інколи сили інерції називають “фіктивними силами”.