ФІЗИКА ДЛЯ БАКАЛАВРІВ. МЕХАНІКА
ІІ. ОСНОВНІ ЗАКОНИ ДИНАМІКИ
2. Сили

Для визначення закону руху тіла необхідно мати повну інформацію про діючі на нього сили, а для цього треба знати загальні властивості та математичні вирази (закони) різних сил.
У макроскопічному світі спостерігається багато різних сил, але всі вони є проявами лише двох фундаментальних взаємодій – гравітаційної та електромагнітної[1]. При цьому
гравітація виявляє себе лишень у силі тяжіння, а всі інші сили мають електромагнітну природу
й зумовлені взаємодією між зарядженими частинками, з яких складаються молекули та атоми речовини. В цьому розділі коротко розглянуто сили, що найчастіше фігурують у задачах механіки:
2.1. Гравітаційна сила та сила тяжіння
2.1. Гравітаційна сила та сила тяжіння
Гравітація є універсальною взаємодією, що полягає в існуванні притягання між будь-яким матеріальним об’єктами. Гравітаційні сили спрямовані по лінії, що проходить через взаємодіючі тіла, і, згідно із законом всесвітнього тяжіння Ньютона, є прямо пропорційні масам тіл m1, m2 і обернено пропорці квадратові відстані r між ними:
|
\( F=G\frac{m_1 m_2}{r^2}, \) |
(2.1) |
Коефіцієнт пропорційності G чисельно дорівнює силі притягання двох тіл із масою по 1 кг, які розміщені на відстані 1 м одне від одного, і називається гравітаційною сталою. Її числове значення складає G = 6,67·10-11 м3/(кг·с2), тож гравітаційні сили є гранично слабкими і відіграють істотну роль лише тоді, коли хоча б одне з тіл має астрономічну масу (планети та зірки).
Слід указати й на те, що величини m1 і m2 в законі всесвітнього тяжіння визначають не інертність тіл, а їхню здатність до взаємного притягання, тобто вони є “гравітаційними” масами тіл, на відміну від “інертних” мас, які фігурують у другому законі Ньютона. Але на досліді встановлено, що гравітаційна та інертна маси є строго прямо пропорційні одна одній. Тому їх не розрізняють і говорять просто про масу тіла та вимірюють в одних і тих самих одиницях. Отже, фізична величина "маса" є і мірою інертності, і мірою здатності тіл до гравітаційної взаємодії.
Використовуючи формулу (2.1), слід пам’ятати, що вона є придатною тільки для матеріальних точок. Виняток складає притягання двох однорідних куль (або кулі та матеріальної точки). В цьому випадку r – це відстань між центрами куль (або центром кулі та матеріальною точкою). Зокрема, це стосується сили тяжіння, тобто сили гравітаційного притягання, що діє на тіла поблизу поверхні планети. Згідно з формулою (2.1) вона визначається як
|
\( F=G\frac{mM}{R^2},\) |
(2.1а) |
де m - маса тіла; М, R - маса і радіус планети.
Гравітаційна сила є прямо пропорційною масі тіла, на яке діє. Тому біля поверхні планети вона надає всім тілам однакового прискорення сили тяжіння
|
\( g= G\frac{M}{R^2},\) |
|
яке напрямлене вертикально вниз. Відповідно, силу тяжіння записують у вигляді
|
\(\vec{F}=m\vec{g}. \), |
(2.2) |
де для Землі принято значення g = 9,806 м/с2 ≈ 9,8 м/с2.
Примітка. Величину g зазвичай називають прискоренням вільного падіння. Загалом, це не точно, позаяк прискорення падаючих тіл відносно Землі приблизно на 0,5% відрізняється від g, позаяк точки земної поверхні самі мають деяке прискорення відносно строго інерціальної системі відліку через добове обертання та орбітальний рух Землі. Але вказана відміна складає всього біля 0,5%, тому в навчальних задачах взагалі часто беруть g = 10 м/с2.
Пружна сила. Пружна сила (сила пружності) виникає при пружних[2] деформаціях тіл, наприклад, при розтягу пружини, або еластичного шнура чи стержня. Вона є зумовлена дією електромагнітних сил взаємодії між молекулами деформованого тіла. Пружна сила завжди напрямлена протилежно до напрямку деформації й за модулем є прямо пропорційною величині деформації (закон Гука). При деформаціях розтягу – стискання величина (модуль) пружної сили
|
\( F=k\Delta{l}, \) |
(2.3) |
де \(\Delta{l}=\left|l-l_0\right| \) – величина деформації, \( l,\,\,\,l_0 \) – довжина деформованої та недеформованої пружини, відповідно, і k – коефіцієнт пропорційності, що називають жорсткістю тіла.
Для стержня (шнура) або пружини з довжиною l і сталою площею перерізу s
|
\( k=E\frac{s}{l}, \) |
(2.4) |
де Е – так званий модуль Юнга, що є табличною характеристикою пружних властивостей речовини тіла. У такому разі вираз закону Гука можна подати у вигляді:
|
\(\sigma=E\epsilon \) або \(\epsilon=\frac{\sigma}{E}, \) |
(2.5) |
де \(\epsilon=\Delta{l}/l_0 \) – відносна деформація і \(\sigma=F/s \) – механічна напруга, що виникає в тілі внаслідок деформації.
Вага тіла, невагомість. Якщо тіло лежить на опорі (чи підвішене на шнурі), то через притягання до Землі воно деформується саме та деформує опору (підвіс). При цьому
сила, що діє з боку тіла на горизонтальну опору або вертикальний підвіс унаслідок притягання до Землі, називається вагою тіла \( \vec{P} \) (рис. 2.3).
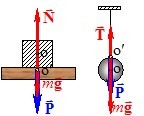
Відповідно, сила, що діє на тіло з боку опори (підвісу) називається реакцією опори \(\vec{N} \) або підвісу \(\vec{T}\). Отже,
вага тіла прикладена не до нього, а до опори чи підвісу.
Якщо опора (підвіс), отож і тіло, не має прискорення відносно інерціальної системи відліку, то \( m\vec{g}+\vec{N}=0 \) i, оскільки \(\vec{N}=-\vec{P} \),
|
\(\vec{P}=m\vec{g},\) |
(2.6) |
тобто, вага тіла дорівнює силі тяжіння, що діє на нього[3]. Але, коли опора (підвіс) має прискорення \(\vec{a}\), то згідно з другим і третім законами Ньютона \( m\vec{a}=m\vec{g}+\vec{N}=m\vec{g}-\vec{P} \), і
|
\(\vec{P}=m(\vec{g}-\vec{a}). \) |
(2.6а) |
Отже,
вага залежить від прискорення опори
і може бути або більшою (при русі вгору), або меншою (при русі вниз), ніж mg. Зокрема, коли опора (підвіс) рухається вниз із прискоренням \(\vec{a}=\vec{g}\) , то \(\vec{P}=0 \), і тіло перебуває в невагомості. При цьому \(\vec{N}=0 \), тобто
в стані невагомості на тіло діє тільки сила тяжіння.
Із залежністю ваги від прискорення опори ми повсякденно стикаємося в ліфті, але особливо відчутно це для космонавтів: вони зазнають великих перевантажень при виході ракети на орбіту та перебувають у невагомості протягом усього часу орбітального польоту.
Сили тертя. З дослідів відомо, що при ковзанні одного тіла по поверхні іншого, або ж при спробах такого руху виникає сила, що перешкоджає рухові. Цю силу називають силою сухого тертя. Якщо ж при спробі примусити одне тіло ковзати по поверхні іншого закріпленого тіла перше залишається у спокої, то тертя, що виникає, називають тертям спокою.
Властивості сил тертя визначаються умовами, за яких вона виникають. Зокрема, сила тертя спокою \(\vec{F}_c \) є рівною по модулю та протилежно напрямленою до рівнодійної решти сил \( \sum\vec{F}_{i} \), які діють на дане тіло, взятій зі знаком мінус:
|
\( \vec{F}_{c}= -\sum\vec{F}_{i} \) |
(2.7) |
Це легко зрозуміти. Якщо тіло знаходиться у спокої, то його прискорення \(\vec{a}=0 \), отже сума сил, що діють на тіло, включно і з силою тертя спокою \(\Sigma(\vec{F}_i+\vec{F}_c)=0 \), звідки й випливає вираз (2.7).
При цьому на досліді встановлено, що величина сили тертя спокою не може перевищувати певного значення
|
\( F_{c\,\max}=\mu{N}, \) |
(2.16) |
де μ – коефіцієнт тертя, який залежить від речовини та стану дотикових поверхонь (зокрема їхньої шорсткості), N – сила нормального тиску, що притискає дане тіло до поверхні іншого. Якщо рівнодійна решти сил, прикладених до тіла, перевищує величину \( F_{c\,\max}\), то воно починає рухатися по поверхні тіла, з яким контактує, й тертя спокою змінюється на тертя ковзання. Величина сили тертя ковзання Fт складно, але досить слабко залежить від відносної швидкості тіл (рис. 2.4а).
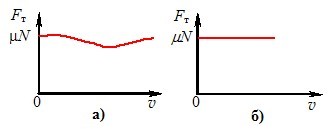
Тому при малих швидкостях її прийнято вважати сталою (рис. 2.4б) і рівною максимальній силі тертя спокою
|
Fт = μN, |
(2.16а) |
|
Сила опору Fоп. Тертя між частинами одного й того ж тіла при їх відносному русі, наприклад, тертя між сусідніми шарами рідини чи газу, що рухаються із різними швидкостями, називають внутрішнім тертям або в’язкістю. Відповідно, при русі тіла в газоподібному чи рідкому середовищі внаслідок взаємодії між його молекулами та молекулами поверхні тіла виникає гальмівна сила, що називається силою опору середовища. При цьому, через слабкий зв’вязок між молекулами та їхню рухливість,
у газах та рідинах не існує тертя спокою.
Сила опору спрямована проти руху тіла й істотно залежить від його швидкості відносно середовища. При малих швидкостях можна вважати, що
|
\({{\vec{F}}_{on}}={{\alpha }}v{{\vec{e}}_{v}}\) |
(2.15) |
де α – стала величина (коефіцієнт опору), залежна від характеристик тіла і середовища, \( \vec{e}_{v} \) – орт вектора швидкості. При великих швидкостях ця залежність є близькою до квадратичної, а при надзвукових — до кубічної
Характерною властивістю сил опору є те, що вони істотно залежать від форми рухомого тіла. Тому рухомим апаратам (авто, літаки, ракети, тощо) надають специфічної обтічної форми.
[1] Фундаментальними називають такі взаємодії, які не зводяться ні до яких інших. Крім вказаних відомі ще два види фундаментальних взаємодій – сильна та слабка, – але в механічних явищах вони ніяк себе не виявляють.
[2] Пружними називають деформації, котрі зникають після припинення дії сили, що їх спричинює.
[3] З цієї причини силу тяжіння інколи теж називають вагою.