ФІЗИКА ДЛЯ БАКАЛАВРІВ. МЕХАНІКА
І. КІНЕМАТИКА
2. Кінематика твердого тіла
Тверді тіла, що рухаються, не завжди можна вважати матеріальними точками. Це стосується, наприклад, рухомих деталей та вузлів механізмів і машин. При цьому різні точки протяжного тіла рухаються не однаково, тому механіка твердого тіла є набагато складніша, ніж механіка точки.
Рух твердих тіл можна поділити на декілька різновидів: 1) поступальний рух; 2) обертання навколо нерухомої осі; 3) плоский рух; 4) обертання навколо нерухомої точки; 5) вільний рух. Але базовими є поступальний і обертальний рухи, позаяк, інші різновиди можна розглядати як сукупність цих двох.
Поступальним називається рух, при якому довільна пряма, проведена між двома точками тіла, в процесі руху не змінює своєї просторової орієнтації. Прикладом може бути рух кузова автомобіля при русі по прямій трасі, або рух кабінки оглядового колеса у парку відпочинку.
Обертальним називають такий рух твердого тіла, коли будь-якої миті всі його точки рухаються по колах із центрами на одній нерухомій прямій – осі обертання.
При поступальному русі всі точки тіла рухаються, як одна, по однакових за формою траєкторіях і з однаковою швидкістю та прискоренням. Отже кінематика поступального руху твердого тіла збігається з кінематикою точки і не потребує окремого розгляду. Шо до інших рухів, то далі заторкуються лише найпростіші — обертальний і плоский рухи.
Розглянуто наступні питання:
2.1. Кутові та лінійні характеристики обертального руху
2.2. Загальні рівняння кінематики обертального руху
2.3. Плоский рух твердого тіла. Миттєва вісь
2.1. Кутові та лінійні характеристики обертального руху
Кутова швидкість. Нехай маємо якесь тіло, що обертається навколо нерухомої осі OZ (рис. 1.8).
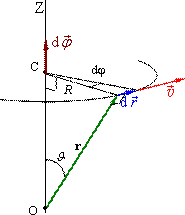
Розглянемо деяку його точку, котра рухається по коловій траєкторії радіуса R із центром у точці С. Задамо положення точки радіусом-вектором \(\vec{r} \) із початком в точці О на осі обертання. За час dt точка здійснює переміщення \( \mathrm{d}\vec{r} \), яке є перпендикулярним до \(\vec{r} \) і має модуль
|
\(\left|\mathrm{d}\vec{r}\right|=R\mathrm{d}\varphi=r\mathrm{d}\varphi\sin\vartheta. \) |
(2.1) |
де \(\mathrm{d}\varphi \) – кут повороту тіла навколо осі обертання за час dt.
Це співвідношення можна подати у векторній формі, аби воно відображало й напрям обертання тіла. Для цього величину dφ розглядають як модуль вектора елементарного кута повороту \( \mathrm{d}\vec{\varphi} \), який напрямлений уздовж осі обертання згідно з правилом правого гвинта.
За цим правилом вектор \( \mathrm{d}\vec{\varphi} \) спрямований у напрямку вкручування правого гвинта при його обертанні в напрямку обертання тіла; подібні вектори називаються аксіальними. Зауважимо також, що відображувати як вектори можна лише нескінченно малі кути повороту.
У такому разі замість виразу (2.1) можна записати:
|
\(\mathrm{d}\vec{r}=\left[\mathrm{d}\vec{\varphi},\vec{r}\right]. \) |
(2.1а) |
Швидкість руху точки отримаємо, поділивши \( \mathrm{d}\vec{r} \) на dt:
|
\(\vec{v}=\left[\frac{\mathrm{d}\vec{\varphi}}{\mathrm{d}t},\vec{r}\right]. \) |
(2.2) |
З цього виразу видно, що різні точки обертового тіла рухаються з різними швидкостями, але перший множник під знаком векторного добутку, однаковий для всіх точок, і тому визначає рух не лишень окремої точки, а й усього тіла. Вектор
|
\(\vec{\omega}=\frac{\mathrm{d}\vec{\varphi}}{\mathrm{d}t}\) |
(2.3) |
називається кутовою швидкістю тіла і є кількісною характеристикою обертального руху .
Вектор \(\vec{\omega} \), як і \(\mathrm{d}\vec{\varphi}\), напрямлений уздовж осі обертання згідно з правилом правого гвинта. Одиницею кутової швидкості є 1 рад/с (радіан за секунду).
Кутове прискорення. Зміна вектора кутової швидкості з часом характеризується вектором кутового прискорення \(\vec{\beta} \):
|
\(\vec{\beta}=\frac{\mathrm{d}\vec{\omega}}{\mathrm{d}t}. \) |
(2.4) |
|
Одиницею кутового прискорення є 1 рад/с2.
При обертанні навколо фіксованої осі вектор \(\vec{\beta} \), так само як і вектор \(\vec{\omega} \), напрямлений уздовж осі обертання (рис. 1.9).
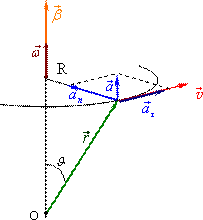
У такому разі зручніше використовувати не вектори, а їхні проєкції на вісь обертання ОZ:
|
\(\omega_z=\frac{\mathrm{d}\varphi}{\mathrm{d}t},\,\,\,\,\,\,\beta_z=\frac{\mathrm{d}\omega_z}{\mathrm{d}t}. \) |
(2.5) |
При цьому, позаяк напрям осі обертання пов’язаний із позитивним напрямом відліку кута повороту правилом правого гвинта. В такому разі знак ωz визначає напрям обертання, а знак βz – характер обертання. До прикладу, на рис. 1.9 відображено прискорене обертання в додатньому напрямі осі ОZ.
Якщо під час руху вісь обертання змінює напрям, то \(\mathrm{d}\vec{\omega} \) і \(\vec{\beta} \) напрямлені під кутом до осі).
Окремим важливим для практики випадком обертального руху є рівномірне обертання тіла навколо фіксованої осі (\(\vec{\beta}=0,\,\,\,\, \vec{\omega}=\mathrm{const} \)). Такий рух є періодичним, отож окрім кутової швидкості його характеризують періодом Т (с) – проміжком часу, за який здійснюється один оберт, і частотою обертання n (1/с) – кількістю обертів за одиницю часу.
Оскільки за один оберт тіло повертається на кут 2π, то
|
\( T=\frac{2\pi}{\omega} \) і \( n=\frac{1}{T}=\frac{\omega}{2\pi}. \) |
(2.6) |
Зв’язок між лінійними та кутовими величинами. При розгляді обертального руху окремих точок твердого тіла величини \(\mathrm{d}\vec{r} \) і \(\vec{v}\) відповідно називають лінійним переміщенням і лінійною швидкістю, на відміну від кутового переміщення \(\mathrm{d}\vec{\varphi} \) та кутової швидкості \(\vec{\omega}\). Між лінійними та кутовими величинами існують однозначні зв’язки. Зокрема, зв’язок між елементарними лінійним і кутовим переміщеннями задається виразами (2.1) і (2.1а), а зв’язок між лінійною та кутовою швидкістю – виразом (2.2) із урахуванням означення (2.3):
|
\(\vec{v}=\left[ \vec{\omega },\vec{r} \right].\) |
(2.7) |
Для модулів маємо:
|
\( v=\omega{r}\sin\vartheta=\omega{R}, \) |
(2.7а) |
де \( {R}=r\sin\vartheta \) – радіус кола, по якому рухається точка.
Вираз для повного прискорення точки через кутові величини знайдемо диференціюванням виразу (2.7):|
\( \vec{a}=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t} \) = \(\left[ \frac{\mathrm{d}\vec{\omega}}{\mathrm{d}t},\vec{r} \right]+\left[\vec{\omega },\frac{\mathrm{d}\vec{r}}{dt} \right] \) = \(\left[ \vec{\beta },\vec{r} \right]+\left[ \vec{\omega },\mathbf{\vec{v}} \right],\) |
де враховано, що \(\mathrm{d}\vec{\omega}/\mathrm{d}t=\vec{\beta} \) – вектор кутового прискорення, а \(\mathrm{d}\vec{r}/\mathrm{d}t=\vec{v} \) – вектор лінійної швидкості.
Оскільки при обертанні тіла навколо нерухомої осі вектори \(\vec{\omega }\) і \(\vec{\beta} \) лежать на осі, то вектор \(\left[\vec{\beta},\vec{r}\right] \) має напрям дотичної до траєкторії даної точки тіла (рис. 1.9) і є її тангенціальним прискоренням \(\vec{a}_{\tau} \):
|
\(\vec{a}_{\tau}=\left[\vec{\beta},\vec{r}\right]. \) |
(2.8) |
При цьому тангенціальне прискорення точки, що обертається, називається її лінійним прискоренням. Його проєкція на напрям дотичної до кола
|
\( a_{\tau}=\beta_z{r}\sin\vartheta=\beta_z{R}. \) |
(2.8а) |
Так само друга складова повного прискорення \(\left[\vec{\omega},\vec{v}\right] \) при нерухомій осі обертання напрямлена по нормалі до траєкторії точки (рис. 1.9), і є її нормальним прискоренням:
|
\(\vec{a}_n=\left[\vec{\omega},\vec{v}\right]. \) |
(2.9) |
Модуль нормального прискорення
|
\( a_n=\omega{v}={\omega}^2 R. \) |
(2.9а) |
На основі співвідношень (2.8а) і (2.9а) можна визначити модуль і напрям (див. рис. 1.9) повного прискорення точок обертового тіла:
|
\( a=\sqrt{a_{\tau}^2+a_n^2}=R\sqrt{{\beta}^2+{\omega}^4}, \) |
(2.10) |
|
|
\(\mathrm{tg}\alpha=\frac{\omega^2}{\beta}. \) |
(2.10а) |
2.2. Загальні рівняння кінематики обертального руху
Кутове прискорення тіла, як і прискорення окремої матеріальної точки, визначається силовою дією на обертове тіло з боку інших тіл, отож його можна знайти, аналізуючи фізичні умови, в яких здійснюється обертання. Тому основною завдачею кінематики обертального руху тіла є визначення решти кутових величин через задане кутове прискорення. При обертанні навколо нерухомої осі це завдання розв’язується так само, як і в кінематиці точки (див. п. 1). При цьому слід завважити, що за загальним змістом і формальними означеннями кутові величини – переміщення \(\mathrm{d}\vec{\varphi} \), швидкість \(\vec{\omega} \) і прискорення \(\vec{\beta} \) – є аналогами відповідних лінійних величин, які характеризують рух матеріальної точки. Тому й
зв’язки між кутовими величинами є аналогічними до зв’язків між аналогічними лінійними величинами.
Через це всі основні рівняння кінематики обертального руху навколо фіксованої осі мають такий самий загальний вигляд, як і відповідні рівнянням кінематики прямолінійного руху точки. Зокрема, проєкція кутової швидкості визначається загальним рівнянням, аналогічним рівнянню для \({{v}_{z}}\) із (1.24):
|
\(\omega_z={\omega}_{0z}+\int\limits_0^t\beta_z\mathrm{d}t, \) |
(2.11) |
де ω0z – проєкція початкової кутової швидкості, βz – проєкція кутового прискорення на напрям осі обертання.
Звідси при βz = const отримуємо рівняння
|
\(\omega_z=\omega_{0z}+\beta_z\int\limits_0^t\mathrm{d}t \) \( \Rightarrow \) \( \omega_z=\omega_{0z}+\beta_z{t}, \) |
(2.11а) |
що є аналогом (1.25а).
Кут повороту (кутове переміщення) φ, який визначає зміну положення тіла відносно осі обертання, знаходиться із загального рівняння
|
\(\varphi=\int\limits_0^t\omega_z\mathrm{d}t. \), |
(2.12) |
яке теж є аналогом рівнянь (1.25) кінематики точки, що визначають зміну положення точки відносно вибраного початку відліку.
При рівнозмінному обертанні \(\beta_z=\mathrm{const} \), і \(\omega_z=\omega_{0z}+\beta_z{t} \). Отже,
|
\(\varphi=\int\limits_0^t\left(\omega_{0z}+\beta_z{t}\right)\mathrm{d}{t}\) \( \Rightarrow \) \( \varphi=\omega_{0z}t+\frac{\beta_z{t}^2}{2}\). |
(2.12а) |
Слід зауважити, що в рівняннях (2.11) – (2.12) величина φ є алгебраїчною, тож число φ/2π не визначає кількості обертів N (повний “шлях”), зроблених тілом за час t. (Виняток становить тільки обертання тіла в незмінному напрямі, коли φ не змінює знаку протягом заданого часу руху). В загальному випадку кількість обертів тіла визначається через модуль кутової швидкості рівнянням
|
\( N=\frac{1}{2\pi}\int\limits_0^t\omega\mathrm{d}t, \) |
(2.12б) |
яке є аналогом рівняння шляху (1.12) в кінематиці матеріальної точки.
2.3. Плоский рух твердого тіла. Миттєва вісь
Плоским називається такий рух, при якому всі точки тіла переміщуються в площинах, паралельних до певної нерухомої в обраній системі відліку площини. Будемо для зручності умовно називати такі площини “площинами руху” точок тіла. Прикладом плоского руху може бути кочення циліндра: всі його точки рухаються в перпендикулярних до осі площинах.
Швидкість точки тіла при плоскому русі. Нехай якесь тіло здійснює плоский рух. Прослідкуємо за відрізком АВ, який з’єднує дві точки цього тіла, що знаходяться в площині руху. За деякий проміжок часу відрізок із положення A1B1, переміщується в положення A2B2 (рис. 1.10).
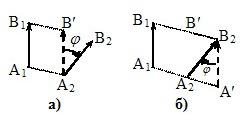
Цю зміну положення можна розглядати як результат поступального переміщення в положення A2B′ і повороту в площині руху на деякий кут φ навколо точки А (рис. 1.10а). Але так само можна говорити про поступальне переміщення відрізка в положення A′B2 та поворот навколо точки В (рис. 1.10б). При цьому переміщення точок А і В – A1A2 і B1B2 – не однакові, але кут повороту φ один і той самий. Зрозуміло, що сказане вірно й для будь якої іншої пари точок і для будь-якого проміжку часу, зокрема, й для нескінченно малого. Тому плоский рух твердого тіла можна розглядати як сукупність поступального руху та обертання навколо фіксованої осі перпендикулярної до площин руху точок тіла. При цьому
кутова швидкість обертання тіла не залежить від вибору такої осі.
Взявши до уваги сказане, розглянемо рух довільної точки А тіла, що здійснює плоский рух в системі відліку XOY (К-система) так, що точки тіла рухаються в площинах, паралельних XOY (рис. 1.11).
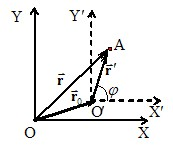
Пов’яжемо з тілом рухому систему відліку X′O′Y′ (K′-система), положення початку відліку котрої O′ в К-системі визначається радіусом-вектором \(\vec{r}_0 \) Положення точки А відносно К-системи відліку визначається радіусом-вектором \(\vec{r} \), а відносно K′-системи – радіусом-вектором \(\vec{r}' \). Очевидно, що
\(\vec{r}=\vec{r}_0+\vec{r}'. \)
Переміщення точки А за нескінченно малий проміжок часу dt
\(\mathrm{d}\vec{r}=\mathrm{d}\vec{r}_0+\mathrm{d}\vec{r}'. \)
Переміщення \(\vec{r}' \) зумовлене поворотом тіла навколо осі, що проходить через точки O′, тому \(\mathrm{d}\vec{r}'=\left[\mathrm{d}\vec{\varphi},\vec{r}'\right] \) (див. (2.1а)). Отже
\(\mathrm{d}\vec{r}=\mathrm{d}\vec{r}_0+\left[\mathrm{d}\vec{\varphi},\vec{r}'\right]. \)
Поділивши останній вираз на проміжок часу dt, одержимо швидкість точки А в К – системі відліку:
|
\(\vec{v}=\vec{v}_0+\left[\vec{\omega},\vec{r}'\right]. \) |
(2.13) |
Таким чином, при плоскому русі швидкість довільної точки А твердого тіла складається із швидкості \(\vec{v}_0 \) будь-якої іншої точки O′, що жорстко зв’язана з ним[5], і лінійної швидкості \(\vec{v}=\left[\vec{\omega},\vec{r}\right] \) обертального руху точки А навколо осі, що проходить через точку O′ перпендикулярно до площини руху.
Миттєва вісь. Оскільки вибір точки O′ є довільним, плоский рух тіла можна звести до чисто обертального. Справді, при плоскому русі вектори \(\vec{v}_0 \) і \(\vec{v}' \) перпендикулярні до вектора кутової швидкості \(\vec{\omega}\) , отже обидва лежать в одній площині руху. Тому в кожну мить існує така жорстко зв’язана з тілом точка М, миттєва швидкість якої \(\vec{v}' \) в К – системі відліку рівна нулю. ЇЇ радіус-вектор \({{\vec{r}}_{m}}^{\prime }\) визначається із співвідношення (2.13):
|
\( {{\vec{v}}_{0}}^{\prime}+\left[\vec{\omega},{{{\vec{r}}}_{m}}^{\prime} \right]=0\quad \Rightarrow \quad \left[\vec{\omega},{{{\vec{r}}}_{m}}^{\prime}\right]=-{{\vec{v}}_{0}}^{\prime} \) |
(2.14) |
Зокрема, модуль \({{\vec{r}}_{m}}^{\prime }\), тобто відстань між точками М і O′, дорівнює:
|
\({{r}_{m}}^{\prime }=\frac{{{v}_{0}}}{\omega }\) |
(2.14а) |
При потребі детальнішої інформації про положення миттєвої осі вираз (2.14) слід розписати в координатній формі за правилами розкриття векторноо добутку
Оскільки точка М у дану мить є нерухомою, то рух тіла в цей момент можна трактувати як чисте обертання навколо осі, що проходить через цю точку перпендикулярно до площини руху. Таку вісь називають миттєвою віссю. В загальному випадку положення миттєвої осі може змінюватися з часом. Наприклад, при коченні циліндра без ковзання по плоскій поверхні миттєва вісь збігається з лінією дотику циліндра до поверхні й рухається із швидкістю осі циліндра. Поняття миттєвої осі є досить продуктивним, оскільки в багатьох випадках спрощує аналіз плоского руху.
- Які види рухів може здійснювати тверде тіло? Які з них можна вважати основними?
- Які величини використовують для опису обертального руху?
- Як напрямлений вектор кутової швидкості твердого тіла?
- Як напрямлений вектор кутового прискорення? В якому випадку вектори кутової швидкості та кутового прискорення є колінеарними? Співнапрямленими?
- Який зв’язок існує між векторами лінійної та кутової швидкості? Між їх модулями?
- Як виражаються тангенціальне, нормальне та повне прискорення точки обертового тіла через кутові характеристики руху?
- Виведіть співвідношення (2.11), (2.11а) і (2.12), (2.12а).
- Який рух твердого тіла називається плоским? Наведіть декілька прикладів.
- Що таке миттєва вісь? Яку перевагу вона дає при розгляді плоского руху тіла?